Download Chapter 9 Systems of Equations

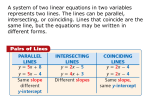
Section 3.5
Systems of Equations
What is a system of
equations?
• Two or more equations in the
same variables
To solve a system
• Find all ordered pairs (x, y) that make both
equations true
Methods to Solve
1. Graphing method
2. Substitution method
3. Linear combination/Elimination
method
Solutions
1. One solution, ordered pair
(intersection of lines)
2. No solution (lines are parallel)
3. Infinitely many solutions
(when same exact line)
Calculator Directions
1. Enter equations in y=
•
y1=1st line and y2=2nd line
2. Hit graph to see lines, change window if
needed
3. Hit 2nd Trace (Calculate)
4. Hit or scroll down to Intersect (#5)
5. Hit enter 3 times to obtain solution
6. Write solution as an ordered pair
Graphing Method
• Graph each line on the same
coordinate plane.
• If lines intersect, there is only one
solution: the intersection point.
• If lines are parallel, there is no
solution.
• If lines coincide, there are infinitely
many solutions.
Substitution Method
• Uses substitution of one equation into
the other to solve for the other
variable
• Goal: Isolate one variable (if not
already given)
• Hint: Isolate the variable that will
allow for easy algebra!
Linear combination
Method
• Add the equations
• Goal: To combine the equations to
eliminate a variable
• Hint: Create coefficients that are
opposites for one of the variables
New Vocab
• Consistent Equations- A system of
equations with at least one solution
– Dependent Equations- A consistent system
with infinitely many solutions (coinciding lines)
• Inconsistent Equations- A system of
equations with no solution
Use intersect, are parallel, or
coincide to make a
true statement
1. If two lines have the same slope and
different y-intercepts, then the lines
are parallel
___________.
1. If one equation can be obtained from
another equation by multiplying both
sides by the same nonzero number, then
the graphs ___________.
coincide
Use intersect, are parallel, or
coincide to make a
true statement
3. If two lines have different slopes and the
same x-intercept, then the lines
__________.
intersect
3. If two lines have more than one point in
common, then the lines ___________.
coincide
5. If the system of equations are dependent,
then the lines ___________.
coincide