* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Elementary Algebra - Seminole State College
Mathematics of radio engineering wikipedia , lookup
Line (geometry) wikipedia , lookup
Elementary mathematics wikipedia , lookup
Recurrence relation wikipedia , lookup
System of polynomial equations wikipedia , lookup
Elementary algebra wikipedia , lookup
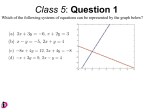
System of linear equations wikipedia , lookup
Elementary Algebra Exam 2 Material Equations • Equation – a statement that two expressions are equal – Equations always contain an equal sign, but an expression does not have an equal sign • Like a statement in English, an equation may be true or false • Examples: 5 9 14 47 5 T or F? T or F? True False . Equations • Most equations contain one or more variables and the truthfulness of the equation depends on the numbers that replace the variables • Example: x 4 9 • What value of x makes this true? x 5 • A number that can replace a variable to make an equation true is called a solution 5 is a solution t o the equation Types of Equations • In Algebra you will study many different types of equations – Learn the names of each type – Learn method for solving each type • The simplest type of equation is called a “linear equation” Linear Equations • Linear equation – an equation where, after parentheses are gone, every term is either a constant, or of the form: cx where c is a constant and x is a variable with exponent1 Linear equations never have a variable in a denominator or under a radical (square root sign) • Examples of Linear Equations: 4 x 5 13 . 3x 7 x 1 3 2 x 3 x 5 1 .72 x 6 x 83 x 2 Identifying Linear Equations • Identify linear equations: x 2 x2 x7 1 x 8 3 2 x5 7 2 x 3 4x 1 x 9 No (exponent 2 on variabl e) Yes (each term is c or cx) No (variable in denominato r) No (variable under radical) Solving Linear Equations • Any equation that is a true statement has both sides with equal values. It is “balanced on both sides of the equal sign.” • In trying to find solutions to an equation we try to do things that will keep both sides of an equation balanced while progressing towards a goal of ending up with the variable alone on one side of the equal sign Solving Linear Equations by Keeping Both Sides Balanced • If we assume that both sides of an equation really are equal and we add or subtract the same thing on both sides, then both sides will still be balanced • In the earlier example, x 4 9 ,what could we have done on both sides of original equation to get a new equation with “x” isolated? Add - 4 (or Subtract 4) x44 94 x 5 Solving an Equation by Balancing with Addition or Subtraction • Solve the equation: x 9 12 x 9 9 12 9 x 3 • The solution to the original equation is: x 3 Solving More Complicated Equations • In solving an equation, make sure that the expression on each side is simplified, before proceeding – Get rid of parentheses – Combine like terms • Next, choose which side will keep the variable and add or subtract terms on both sides, as necessary, to isolate the variable 2x 3 5x 4x 2 2 x 6 5x 4 x 8 2x 6 x 8 2x 6 x x x 8 x 6 8 x 6 6 . 8 6 x 2 English Sentences that Translate to Equations • If an English sentence indicates that two numerical expressions are equal, it can be translated to an equation • The phrases: “the result is”, or “is equal to”, “equals” or “is”, can usually be translated into algebra as an equal sign, = • Translate: The sum of a number and three is 15. x 3 15 Translating Sentences to Equations and Solving • The major reason for translating a sentence to an equation is to help us find the value of an unknown number described in the sentence • Find the unknown number in the previous example: “The sum of a number and 3 is 15”: x 3 15 x 3 3 15 3 x 12 The number described must be 12. Other Examples of Translating English Sentences to Equations • Translate and Solve: The product of 3 and a number is equal to twice the number plus 7. 3x 2x 7 3x 2x 2x 2x 7 x7 The number described must be 7. Other Examples of Translating English Sentences to Equations • Translate and Solve: Twice the sum of a number and 5 is the same as 8 less than the number. What is the number? 2x 5 x 8 2x 10 x 8 2x x 10 x x 8 x 10 8 x 10 10 8 10 x 18 The number described must be -18. Homework Problems • Section: • Page: • Problems: 2.1 100 Odd: 5 – 43, 47 – 65, All: 69 – 72 • MyMathLab Section 2.1 for practice • MyMathLab Homework Quiz 2.1 is due for a grade on the date of our next class meeting Another Way to Keep Equations Balanced • We have learned that equations that are true statements can be kept balanced by adding or subtracting the same thing on both sides of equal sign • We can also keep both sides balanced by multiplying or dividing both sides by any number that is not zero • Examples follow that show how multiplying or dividing can help solve an equation Solving Equations Using Multiplication or Division • Solve: 1 x 5 3 • The equation will be solved when we have 1 x by itself , not x 3 • What could we multiply on both sides? 3 1 3 x 3 5 3 x 15 Solving Equations Using Multiplication or Division • Solve: 2 x 12 • The equation will be solved when we have x by itself , not 2 x • What could we divide on both sides? 2 2 x 12 2 2 x 6 Other Examples of Translating English Sentences to Equations • Translate: The difference between 4 and a number equals the number plus 5. 4 x x 5 4 x x x x 5 4 2x 5 1 2x 5 subtracted from both sides 1 2x 2 2 1 The number described must be - . 2 Other Examples of Translating English Sentences to Equations • Translate: If 11 times a number is subtracted from 8 times the number, the result is -9. 8x 11x 9 3x 9 3x 9 3 3 x 3 The number described must be 3. Homework Problems • Section: 2.2 • Page: 107 • Problems: Odd: 7 – 69, All: 73 – 76 • MyMathLab Section 2.2 for practice • MyMathLab Homework Quiz 2.2 is due for a grade on the date of our next class meeting Solving Linear Equations • Simplify each side separately – Get rid of parentheses – Multiply by LCD to get rid of fractions and decimals – Combine like terms • Get the variable by itself on one side by adding or subtracting the same terms on both sides • If the coefficient of the variable term is not 1, then divide both sides by the coefficient Determine if the equation is linear. If it is, solve it: Is it linear? Yes 23x 1 4x 8 6x 2 4x 8 6x 4x 2 4x 4x 8 2x 2 8 2x 2 2 8 2 2 x 6 2x 6 2 2 x 3 Determine if the equation is linear. If it is, solve it: Is it linear? Yes 8 6x 5 7 2x 4 8 6x 30 7 2x 8 6x 38 2x 1 6x 2x 38 2x 2x 1 8x 38 1 8x 38 38 1 38 8x 37 8 x 37 37 x 8 8 8 Determine if the equation is linear. If it is, solve it: Is it linear? Yes 24 3x 3x 1 14 8 6x 3x 3 14 8 6x 3x 17 8 9x 17 9 9x 1 x Determine if the equation is linear. If it is, solve it: Is it linear? No 2 x 3 5x x 2 4 • We can’t solve this equation yet. Later we will learn its name, and how to solve it! Determine if the equation is linear. If it is, solve it: Is it linear? Yes 2 1 x x 2 0.3 x 1 3 4 2 1 1 3 x x x 1 3 4 2 10 1 1 2 3 60 x x 60 x 1 4 2 3 10 40x 15x 30 18x 60 25x 30 18x 60 7 x 30 60 7 x 90 90 x 7 Example • Solve: • LCD: 5 3 x x2 6 4 6 2 3 4 22 LCD 2 2 3 12 • Multiply both sides by LCD: 5 3 12 x 12 x 2 6 4 10x 9x 24 x 24 Example • Solve: • LCD: 7 5 x 3 x 1 24 9 24 2 2 2 3 9 3 3 LCD 2 2 2 3 3 72 • Multiply both sides by LCD: 7 5 72 x 3 72 x 1 24 9 21x 216 40x 72 216 19x 72 288 19 x 288 x 19 Example • Solve: .3x 7 .52x .13 • LCD: 10 100 LCD 2 5 2 255 2 2 5 5 100 The LCD of multiples of 10 is always the largest multiple • Multiply both sides by LCD: 100.3x 7 100.52x .13 30x 700 52x 13 700 22x 13 713 22x 713 x 22 Example with Fractions & Decimals • Solve: • LCD: 1 3 x .3 x 5 6 4 6 2 3 4 22 10 2 5 LCD 2 2 3 5 60 • Multiply both sides by LCD: 3 1 60 x 60.3x 5 4 6 10x 45 18x 300 45 8x 300 345 8x 345 x 8 Linear Equations with No Solution or All Real Numbers as Solutions • Many linear equations only have one number as a solution, but some have no solution and others have all numbers as solutions • In trying to solve a linear equation, if the variable disappears (same variable & coefficient on both sides) and the constants that are left make a statement that is: – false, the equation has “no solution” (no number can replace the variable to make a true statement) – true, the equation has “all real numbers” as solutions (every real number can replace the variable to make a true statement) Solve the Linear Equation 2x x 3 x 7 2x x 3 x 7 x 3 x 7 x x 3 x x 7 37 False! Equation has no solution Solve the Linear Equation x 2 7 x 2x 21 3x x 2 7 x 2x 2 6x 8x 2 8x 2 8x 8x 2 8x 8x 2 2 2 True! All real numbers are solutions Homework Problems • • • • • Section: Page: Problems: Page: Problems: 2.3 115 Odd: 7 – 45 117 Odd: 1 – 29 • MyMathLab Section 2.3 for practice • MyMathLab Homework Quiz 2.3 is due for a grade on the date of our next class meeting Solving Application Problems • Some problems may involve more than one sentence and more than one unknown • Such problems may seem as overwhelming as trying to eat an elephant • How do you eat an elephant? One bite at a time! • Application problems are solved easily if you memorize the steps and do them one at a time! Steps in Solving Application Problems • Read the problem carefully trying to understand what the unknowns are (take notes, draw pictures, don’t try to write equation until all other steps below are done ) • Make word list that describes each unknown • Assign a variable name to the unknown you know the least about (the most basic unknown) • Write expressions containing the variable for all the other unknowns • Read the problem one last time to see what information hasn’t been used, and write an equation about that • Solve the equation (make sure that your answer makes sense, and specifically state the answer) Example of Solving an Application Problem • Three less than 5 times a number is equal to 9 less than twice the number. What is the number? • List of unknowns This is the only unknown so we call it : – A number x • What else does the problem tell us that we haven’t used? Three less than 5 times a number is equal to 9 less than twice the number. • What equation says this? 5x 3 2 x 9 Example Continued 5x 3 2 x 9 5x 2 x 3 2 x 2 x 9 3x 3 9 3x 3 3 9 3 3x 6 x 2 • Solve the equation: • Answer to question? The number described is: 2 Example of Solving an Application Problem With Multiple Unknowns • A mother’s age is 4 years more than twice her daughter’s age. The sum of their ages is 76. What is the mother’s age? • List of unknowns – Mother’s age 2x 4 – Daughter’s age x Which do we know least about? Daughter' s age • What else does the problem tell us that we haven’t used? Sum of their ages is 76 • What equation says this? x 2x 4 76 Example Continued • Solve the equation: x 2x 4 76 3x 4 76 3x 4 4 76 4 3x 72 x 24 • Answer to question? Mother’s age is 2x + 4: 224 4 52 Solve the Application Problem • A 31 inch pipe needs to be cut into three pieces in such a way that the second piece is 5 inches longer than the first piece and the third piece is twice as long as the second piece. How long should the third piece be? 1. Read the problem carefully taking notes, drawing pictures, thinking about formulas that apply, making charts, etc. Perhaps draw a picture of a pipe that is labeled as 31 inches with two cut marks dividing it into 3 pieces labeled first, second and third 1st 2nd 3rd 31 Example Continued 2. Read problem again to make a “word list” of everything that is unknown What things are unknown in this problem? The length of all three pieces (even though the problem only asked for the length of the third). Word List of Unknowns: Length of first Length of second Length of third Example Continued 3. Give a variable name, such as “x” to the “most basic unknown” in the list (the thing that you know least about) What is the most basic unknown in this list? Length of first piece is most basic, because problem describes second in terms of the first, and third in terms of second Give the name “x” to the length of first Example Continued 4. Give all other unknowns in the word list an algebraic expression name that includes the variable, “x” How would the length of the second be named? x+5 How would the length of the third be named? 2(x + 5) Word List of Unknowns: Algebra Names: Length of first x Length of second x+5 Length of third 2(x + 5) Example Continued 5. Read the problem one last time to determine what information has been given, or implied by the problem, that has not been used in giving an algebra name to the unknowns and use this information to write an equation about the unknowns What other information is given in the problem that has not been used? Total length of pipe is 31 inches How do we say, by using the algebra names, that the total length of the three pieces is 31? x + (x + 5) + 2(x + 5) = 31 Example Continued 6. Solve the equation and answer the original question This is a linear equation so solve using the appropriate steps: x + (x + 5) + 2(x + 5) = 31 x + x + 5 + 2x + 10 = 31 4x + 15 = 31 4x = 16 x=4 Is this the answer to the original question? No, this is the length of the first piece. How do we find the length of the third piece? The length of the third piece is 2(x + 5): 2(4 + 5) = (2)(9) = 18 inches = length of third piece Solving Application Problems Involving Angles • Angles are measured in units called degrees • A complete rotation of a ray from a starting position back to the starting position has a measure of 360o • Half of a rotation of a ray from a starting position to a position pointing the opposite direction has a measure of 180o and the angle is called a straight angle • One quarter of a rotation of a ray has a measure of 90o and the angle is called a right angle • Two angles whose sum makes a right angle (whose sum is 90o) are called complementary angles • Two angles whose sum makes a straight angle (whose sum is 180o) are called supplementary angles • If x represents the measure of an angle, – The measure of the complementary angle is: – The measure of the supplementary angle is: 90 x 180 x Example of Solving an Angle Application Problem • Find the measure of an angle such that the supplement is 15o more than twice the complement • List of unknowns – Angle measure – Complement measure – Supplement measure x 90 x 180 x Which do we know least about? Measure of angle • What else does the problem tell us that we haven’t used? Supplement is 15o more than twice the complement • What equation says this? 180 x 290 x 15 Example Continued • Solve the equation: 180 x 290 x 15 180 x 180 2x 15 x 2x 15 x 15 • Answer to question? o The measure of the angle is: 15 Solving Application Problems Involving Consecutive Integers • If an application problem involves consecutive integers, consecutive even integers, or consecutive odd integers, remember that consecutive integers differ by 1 and consecutive even, as well as consecutive odd, integers differ by 2 • If x represents an integer, the next integer is x + 1, and the next is x + 2, etc • If x represents an even integer, the next even integer is x + 2, and the next is x + 4, etc • If x represents an odd integer, the next odd integer is x + 2, and the next is x + 4, etc Example of Solving a Consecutive Integer Application Problem • Find two consecutive odd integers such that three times the smaller is thirteen less than twice the larger • List of unknowns – smaller odd integer x – next larger odd integer x2 Which do we know least about? First odd integer • What else does the problem tell us that we haven’t used? Three times smaller is 13 less than twice larger • What equation says this? 3x 2x 2 13 Example Continued • Solve the equation: 3x 2x 2 13 3x 2x 4 13 3x 2x 9 x 9 • Answer to question? The smaller odd integer is x = 9 7 The larger odd integer is x + 2 = Homework Problems • • • • • Section: 2.4 Page: 126 Problems: Odd: 11 – 57 MyMathLab Section 2.4 for practice MyMathLab Homework Quiz 2.4 is due for a grade on the date of our next class meeting