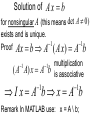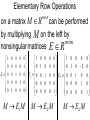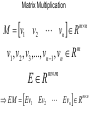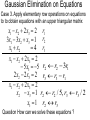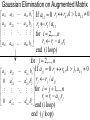Download CZ2105 Lecture 2 - National University of Singapore

MA2213 Lecture 5
Linear Equations
(Direct Solvers)
Systems of Linear Equations p. 243-248
Occur in a wide variety of disciplines
Anthropology Astronomy Archaeology
Biology
Business Chemistry
Economics Engineering Finance
Geology Mathematics Management
Medicine Physics
Sociology
Psychology
Statistics
Matrix Form
for a system of
linear equations
Ax  b
nn
A R
n
bR
n
xR
coefficient matrix
(right) column vector
(solution) column vector
Linear Equations in Mathematics
Numerical Analysis
Interpolation
Vandermonde (for polyn. interp.)
T
B B or Gramm
Least Squares
Quadrature
Geometry
Algebra

a b  0
a b  2
Coefficient Matrix
Transpose of Vandermonde
Lec 4 vufoil 13 (to compute weights)
find intersection of lines or planes
partial fractions

2
a
b


2
x 1 x 1 x 1
1 1  a  0
1  1 b   2 

   
a 1
b  1
Matrix Arithmetic p. 248-264
mn
m p
A

R
 AB  R
Matrix Multiplication
n p
BR
Identity Matrix
I2
Matrix Inverse
a
c

1 0 0
1 0 


I 3  0 1 0


0 1 
0 0 1
1
b
1  d  b


d
ad  bc  c a 
Theorem 6.2.6 p. 255 A square
matrix has an inverse iff (if and only if)
its determinant is not equal to zero.
Solution of A x  b
for nonsingular A (this means det A  0)
exists and is unique.
Proof
1
1
Ax  b  A ( A x)  A b
1
1
( A A) x  A b
1
multiplication
is associative
1
I x A bx A b
Remark In MATLAB use: x = A \ b;
Column Rank of a Matrix
Definition The column rank of a matrix
mn
M  R , cr M {0,1,..., m} is the
m1
dimension of the subspace of R  R
spanned by the column vectors of M
Remark cr M  maximal number of
linearly independent column vectors
of M
m
Question
 2 4 2
cr 

?

1 2 0 
Row Rank of a Matrix
Definition The row rank of a matrix
mn
M  R , rr M {0,1,..., n}
n1
is the dimension of the subspace of R
spanned by the row vectors of M
Remark rr M  maximal number of
linearly independent row vectors of M
Question
 2 4 2
rr 

?

1 2 0
A Matrix Times a Vector
The equation  a11
a
21

Ax  b 
 

an1
 a11 
a 
21 

x1
 x2
  
 
an1 
a12
a22

an 2
 a1n   x1   b1 





 a2 n   x2  b2 

   
   
 ann   xn  bn 
 a12 
a 
 22     x
n
  
 
 an 2 
 a1n   b1 
a  b 
 2n    2 
   
   
 ann  bn 
has solution iff b is a linear combination of columns of A
Existence of Solution in General
The linear equation
Ax  b
has a solution if and only if
called Augmented
matrix p. 265
cr [ A b ]  cr A
EVEN IF
A
IS SINGULAR!
2 4   x1   b1 

1 2   x  b 

 2   2 
Example
this has a solution iff
b1  2b2
then it has an infinite
number of solutions
Computing the Column and Row Ranks
mn
The ranks of a matrix M  R
can be computed using a sequence of
elementary row operations p. 253-254.
i. Interchange two rows
ii. Multiply a row by a nonzero scalar
iii. Add a nonzero multiple of one row
to another row
Question Show that each of the ERO
i, ii, iii has an inverse ERO i, ii, iii.
Elementary Row Operations
mn
on a matrix M  R can be performed
by multiplying M on the left by
mm
nonsingular matrices E  R
1
0

Ei  0

0
0
0 0 0 0
1
0
0 0 0 1

0 1 0 0 Eii  0


0 0 1 0
0
1 0 0 0
0
M  Ei M
0 0 0 0
1
0
1 0 0 0

0 1 0 0 Eiii  0


0 0 5 0
0
0
0 0 0 1
M  Eii M
0 0
1 0
0 1
0 0
0 0
0
 2 0
0 0

1 0
0 1
0
M  Eii M
Invariance of Row Rank Under ERO
mm
mn
Theorem 1. If M  R
and E  R
is an ERO matrix, then rr E M  rr M .
Proof Clearly, interchanging two rows
and multiplying a row by a nonzero
scalar does not change the row rank.
Finish the proof by showing that
adding a multiple of any row to another
row does not change the row rank.
Remark Clearly the row rank of a matrix
is invariant under sequence of ERO’s.
Matrix Multiplication
M  v1 v2  vn  R
v1 , v2 , v3 ,..., vn 1 , vn  R
ER
 EM  Ev1
mn
m
mm
Ev2  Evn  R
mn
Invariance of Column Rank under ERO
mm
mn
Theorem 2 If M  R
and E  R
is nonsingular then cr E M  cr M .
Proof It suffices to show that for a set
of column vectors vk , vk ,..., vk of M
1
2
r
are linearly dependent iff the set of
column vectors Evk1 , Evk2 ,..., Evkr of E M
are linearly dependent. Show why it
suffices and then show it. Hint: prove
c1 Evk1    cr Evkr  0  c1vk1    cr vkr  0
Row Echelon Matrices
mn
Definition A matrix M  R
is called
an row echelon matrix if
i. the nonzero rows come first
ii. the first nonzero element in each row
=1 (called a pivot) has all zeros below it
iii. each pivot lies to the right of the
pivot in the row above
Row Echelon Matrices
These three properties produce a
staircase pattern in the matrix below
1
0

0

0

0
3 8.6 0
5
1
6
1
3
0
0
0
0
1 3
0 0
2
0
5
0
0
0
0
0
0
0
1
4
 9.7 0
13 

4  4
7 0 

1
6
0
0 
5
Question Where are the pivots ?
Row Rank of an Row Echelon Matrix
equals the number of nonzero rows.
1
4 5 13 
1 3 8.6 0 5
0 1 6 1 3  9.7 0 4  4


0 0 0 1  3
2
5 7 0 


0
0 1
6
0 0 0 0 0
0 0 0 0 0
0
0 0
0 
Question What is the rank of this matrix ?
Prove this by showing that the rows must
be linearly independent. Hint : use pivots.
Col. Rank of a Row Echelon Matrix
equals the number of nonzero rows.
1
0

0

0
0
3 8.6 0
5
1
6
1
3
0
0
0
0
1 3
0 0
2
0
5
0
0
0
0
0
0
0
1
4
 9.7 0
13 

4  4
7 0 

1
6
0
0 
5
Question Show this by showing that the col.
vectors that contain pivots form a basis for
the space spanned by col. vectors. Hint: do
elem. col. operations on the matrix above.
Reduction to Row Echelon Form
Theorem 3 For every matrix M  R mn
mm
there exists a nonsingular matrix E  R
such that E M is an echelon matrix.
Furthermore, the matrix E is a product
E  E1E2 E3 E4  Ek where each
E j , 1  j  k is an ERO matrix.
Application of the sequence of ERO’s is
called reduction to row echelon form.
Proof Based on Gaussian elimination.
Row Rank = Column Rank
Theorem 4 For every matrix M  R mn
cr M  rr M
Proof. Theorem 3 implies that there exists
a product E  E1 E2 E3 E4  Ek
of ERO matrices such that E M is a row
echelon matrix. Theorems 1 implies that
rr M  rr EM and theorems 2 implies that
cr M  cr EM. Since E M is a row echelon
matrix, rr E M  cr EM hence rr M  cr M .
Applications of Row Echelon Reduction
The linear equation
Ax  b
iff the last nonzero row of the reduced
has a solution
E[A b]
has its pivot NOT in the last column.
Example
b1
b1




1 2
2 4 b1 
1 2 2
2


 
1 2 b  
b1 
2

1 2 b2  0 0 b2  2 
Hence the condition above is satisfied iff
b2   0.
b1
2
Applications of Row Echelon Reduction
A basis of column vectors for a matrix
M R
mn
can be obtained by first computing the reduction
E M  [v1 , v2 ,..., vn ] then choosing the column vectors
vk1 , vk 2 ,..., vk r that contain the pivots. Then the vectors
1
1
1
E vk1 , E vk2 ,..., E vkr are column vectors of M
that form a basis for the space spanned by the column
vectors of
M.
Generalities on Gaussian Elimination
Gaussian elimination is the process of reducing a matrix
to row echelon form through a sequence of ERO’s.
It can also be used to solve a system of linear equations
It is ‘best’ taught through showing examples.
We will show how to solve a system of linear equations
using Gaussian elimination, it will become obvious how
to use Gaussian elimination for reduction.
The final step of solving a system of equations after the
augmented matrix has been reduced is called back
substitution, this process is related to elementary column
operations and will be addressed in the homework.
Gaussian Elimination (p. 264-269)
a11 0
0 a
22

A



0
0
Case 1.
 0

 0
  

 ann 
Question What type
of matrix is this ?
The equations for this matrix are
a11x1  b1 , a22 x2  b2 ,..., ann xn  bn
therefore, if A is nonsingular then
bn
b1
b2
x1 
, x2 
,..., xn 
a11
a22
ann
Question How do we use the nonsingular assumption?
Back Substitution
a11 a12

Case 2.
0 a
22

A



0
0
 a1n  Question What is
 a2 n  this matrix called ?
   Question What are the
 associated equations ?
 ann 
A nonsingular  solution by back-substitution p. 265
1
nn n
1
n 1,n1
xn  a b
xn1  a
[ bn1  an1,n xn ]

1
x1  a11 [ b1  a12 x2  a13 x3    a1n xn ]
Question How do we use the nonsingular assumption?
Question Why is this method called back-substitution ?
Gaussian Elimination on Equations
Case 3. Apply elementary row operations on equations
to to obtain equations with an upper triangular matrix
x1  x2  2 x3  2 r1
3x1  3x2  x3  1 r2
x1  x2
 4 r3
x1  x2  2 x3  2
 5 x3  5 r2  r2  3r1
2 x2  2 x3  2 r3  r3  r1
x1  x2  2 x3  2
x2  x3  1 r2  r2 / 5, r3  r3 / 2
x3  1 r2  r3
Question How can we solve these equations ?
Gaussian Elimination on Augmented Matrix
 a11 a12  a1n b1  If a11  0 r1  rk , k  1, a k 1  0
a

 21 a22  a2 n b2  r1  r1 / a11
 
     for i  2,..., n


ri  ri  a i1r1
an1 an 2  ann bn 
end (i loop )

for j  2,..., n
a11 a12  a1n b1  If a jj  0 rj  rk , k  j , a k j  0
 0 a1  a1 b1  r j  r j / a jj
22
2n 2 


     for i  j  1,..., n
ri  ri  a i j r j

1
1
1
 0 an 2  ann bn  end (i loop)
end ( j loop)
Gaussian Elimination
1  1 2 2
3  3 1 1


1 1 0 4

r2  r2  3r1
r3  r3  r1
1
r


2 2
1  1 2
5 R2
0 0  5  5
1

 r3  2 r3
0 2  2 2 
r2  r3

1  1 2 2
0 1  1 1


0 0 1 1
r2  r2  3r1
Ax  b

EAx  Eb
Question What is the solution ?
Partial Pivoting p. 270-273
For the j-th column in Gaussian elimination compute
the integer
jkn
that gives
then perform the row interchange
S j  max | a j k |
1 k  n
rj  Rk
Read p. 273-276 about how Gaussian elimination
can be used to compute the inverse of a matrix.
LU Decomposition p. 283-285
Ax  b for many values of b with same A
first compute the factorization A  L U where
To solve
0
1

1
21
L
 


 n1  n 2




0
u11 u12


0
0
u
22

U





1
0
0
 u1n 

 u2 n 
  

 unn 
Then for each b use forward substitution to solve L y = b
then use backward substitution to solve U x = y.
LU Decomposition Algorithm
Algorithm
Step 1
u1 j  a1 j , j  1,..., n
 i1  ai1 / u11 , i  2,..., n
Step 2 for r = 2,…,n do
r 1
u r j  ar j    r k u k j , r  j  n
k 1
r 1


1
 i r  urr  ai r    i k uk r  , r  1  i  n
k 1


Question How many operations does this require ?
Homework Due Tutorial 3
Question 1. Prove that the row rank of an row echelon
matrix equals the number of nonzero rows.
Question 2. Prove that the column rank of an row
echelon matrix equals the number of nonzero rows by
showing that the set of its column vectors having pivots
is a maximal set of linearly independent column vectors.
Question 3. Use Gaussian elimination to solve
2u2  4u3  28, 3u1  6u2  9u3  54, 5u1  6u2  15u3  90
Question 4. Derive expressions for the entries of the L
and U in the LU decomposition of a 3 x 3 matrix A.
Question 5. Show how elementary column operations
can be applied to a row echelon matrix M to obtain a row
echelon matrix with exactly one 1 in each nonzero row.
Use this to determine a basis for the space { x : Mx = 0 }.