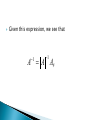* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Capelli's identity wikipedia , lookup
Euclidean vector wikipedia , lookup
System of linear equations wikipedia , lookup
Quadratic form wikipedia , lookup
Tensor operator wikipedia , lookup
Covariance and contravariance of vectors wikipedia , lookup
Rotation matrix wikipedia , lookup
Jordan normal form wikipedia , lookup
Eigenvalues and eigenvectors wikipedia , lookup
Linear algebra wikipedia , lookup
Bra–ket notation wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Basis (linear algebra) wikipedia , lookup
Matrix (mathematics) wikipedia , lookup
Cartesian tensor wikipedia , lookup
Singular-value decomposition wikipedia , lookup
Non-negative matrix factorization wikipedia , lookup
Perron–Frobenius theorem wikipedia , lookup
Determinant wikipedia , lookup
Four-vector wikipedia , lookup
Cayley–Hamilton theorem wikipedia , lookup
Lecture XXVI
The material for this lecture is found in James
R. Schott Matrix Analysis for Statistics (New
York: John Wiley & Sons, Inc. 1997).
A matrix A of size m x n is an m x n
rectangular array of scalars:
a11 a12
a
a
21
22
A
am1 am 2
a1n
a2 n
amn
It is sometimes useful to partition matrices
into vectors.
a11
a
A 21
am1
a12
a22
am 2
a1n
a2 n
a1
amn
a1
a
2
a3
a2 an
a1 j
a
2j
a j
or ai ai1 ai 2 aim
amj
The sum of two identically dimensioned
matrices can be expressed as
A B aij bij
In order to multiply a matrix by a scalar,
multiply each element of the matrix by the
scalar.
In order to discuss matrix multiplication, we
first discuss vector multiplication. Two
vectors x and y can be multiplied together to
form z (z=x y) only if they are conformable.
If x is of order 1 x n and y is of order n x 1,
then the vectors are conformable and the
multiplication becomes:
n
z x y xi yi
i 1
Extending this discussion to matrices, two
matrices A and B can be multiplied if they are
conformable. If A is order k x n and B is of
order n x l. then the matrices are
conformable. Using the partitioned matrix
above, we have
a1
a
2
b1 b2
C AB
ak
a1b1 a1b2
a b a b
2 2
2 1
ak b1 ak b2
bl
a1bl
a2bl
ak bl
Theorem 1.1 Let a and b be scalars and A, B,
and C be matrices. Then when the operations
involved are defined, the following properties
hold:
◦
◦
◦
◦
◦
A+B=B+A.
(A+B)+C=A+(B+C).
a(A+B)=aA+aB.
(a+b)A=aA+bA.
A-A=A+(-A)=(0).
◦ A(B+C)=AB+AC.
◦ (A+B)C=AC+BC.
◦ (AB)C=A(BC).
The transpose of an m x n matrix is a n x m
matrix with the rows and columns
interchanged. The transpose of A is denoted
A’.
Theorem 1.2 Let a and b be scalars and A and
B be matrices. Then when defined, the
following hold
◦
◦
◦
◦
(aA)’=aA’.
(A’)’=A.
(aA+bB)’=aA’+bB’.
(AB)’=B’A’.
The trace is a function defined as the sum of
the diagonal elements of a square matrix.
m
tr A aii
i 1
Theorem 1.3 Let a be scalar and A and B be
matrices. Then when the appropriate
operations are defined, we have
◦
◦
◦
◦
◦
tr(A’)=tr(A).
tr(aA)=atr(A).
tr(A+B)=tr(A)+tr(B).
tr(AB)=tr(BA).
tr(A’A)=0 if and only if A=(0).
Traces can be very useful in statistical
applications. For example, natural logarithm
of the normal distribution function can be
written as:
1
1
1
n , mn ln 2 n ln tr 1Z
2
2
2
n
Z yi yi '
i 1
◦ Jan R. Magnus and Heinz Neudecker Matrix
Differential Calculus with Applications in Statistics
and Econometrics (New York: John Wiley & Sons,
1988) p. 314.
The Determinant is another function of
square matrices. In its most technical form,
the determinant is defined as:
A 1
1
f i1 ,i2 ,im
f i1 ,i2 im
a1i1 a2i2 amim
ai11ai2 2 aim m
where the summation is taken over all
permutations, (i1,i2,…im) of the set of integers
(1,…m), and the function f(i1,i2,…im) equals the
number of transpositions necessary to change
(i1,i2,…im).
In the simple case of a 2 x 2, we have two
possibilities (1,2) and (2,1). The second
requires one transposition. Under the basic
definition of the determinant:
A 1 a11a22 1 a12a21
0
1
In the slightly more complicated case of a 3 x
3, we have six possibilities (1,2,3), (2,1,3),
(2,3,1), (3,2,1), (3,1,2), (1,3,2). Each one of
these differs from the previous one by one
transposition. Thus, the number of
transpositions are 0, 1, 2, 3, 4, 5. The
determinant is then defined as:
A 1 a11a22a33 1 a12a21a33 1 a12a23a31
0
1
2
1 a13a22a31 1 a13a21a32 1 a11a23a32
3
4
5
a11a22a33 a12a21a33 a12a23a31 a13a22a31 a13a21a32
a11a23a32
A more straightforward definition involves the
expansion down a column or across the row.
◦ In order to do this, I want to introduce the concept
of principal minors.
The principal minor of an element in a matrix is the
matrix with the row and column of the element
removed.
The determinant of the principal minor times negative
one raised to the row number plus the column number
is called the cofactor of the element.
◦ The determinant is then the sum of the cofactors
times the elements down a particular column or
across the row:
m
A aij Aij aij 1 mij
j 1
i j
In the three by three case:
A a11 1
11
a22
a32
a31 1
31
a23
2 1 a12
a21 1
a33
a32
a12
a22
a13
a33
a13
a23
A a11a22a33 a11a23a32 a12a21a33 a13a21a32
a12a23a31 a13a22a31
Theorem 1.4 If a is a scalar and A is an m x m
matrix, then the following properties hold:
|A’|=|A|.
|aA|=am|A|.
If A is a diagonal matrix, then |A|=a11a22…amm.
If all elements of a row (or column) of A are zero,
|A|=0.
◦ If two rows (or columns) of A are proportional to
one another, |A|=0.
◦
◦
◦
◦
◦ The interchange of two rows (or columns) of A
changes the sign of |A|.
◦ If all the elements of a row (or column) of A are
multiplied by a, then the determinant is multiplied
by a.
◦ The determinant of A is unchanged when a multiple
of one row (or column) is added to another row (or
column).
Any m x m matrix A such that |A|≠0 is said
to be a nonsingular matrix and possesses an
inverse denoted A-1.
1
1
AA A A I m
Theorem 1.6 If a is a nonzero scalar, and A
and B are nonsingular m x m matrices, then
◦
◦
◦
◦
◦
◦
◦
(aA)-1=a-1A-1.
(A’)-1=(A-1)’.
(A-1)-1=A.
|A-1|=|A|-1.
If A=diag(a11,…amm), then A-1=diag(a11-1,…amm-1).
If A=A’, then A-1=(A-1)’.
(AB)-1=B-1A-1.
The most general definition of an inverse
involves the adjoint matrix (denoted A#). The
adjoint matrix of A is the transpose of the
matrix of cofactors of A. By construction of
the adjoint, we know that:
AA# A# A diag A , A , A A I m
In order to see this identity, note that
aibi A where B A#
a j bi 0 where B A# and i j
Focusing on the first point
AA# 11 a11
a12
1 a11
11
1
1 3
a13
11 a22
1
a32
1 2 a21
a13 1
a31
1 3 a21
1
a31
a22
a23
a32
a33
a21 a22
a31
a32
a23
a33
a23
a33
a22
a32
1 a12
1 2
A
a21 a23
a31
a33
Given this expression, we see that
1
1
A A A#
1 0 0 1 9
3 1 0 3 7
2 0 1 2 3
9
1
1
0
20
0 1
0 0
20
0 15
1 0
20
5 1 0 0
8 0 1 0
5 0 0 1
0 0
20 7 3 1 0
15 5 2 0 1
9
5
1
1 0 37 1
5
0 1 7 0
5
4 0
0 0
1 0
0 1
0 0
9
0 37
7
0
20
20
20
3
1 7
1
0
20
20
20
1
0 1
3
1
4
4
4
0 11
6 37
5
5
0 1
1 7
5
5
1
1
3
4
The rank of a matrix is the number of linearly
independent rows or columns. One way to
determine the rank of any general matrix m x
n is to delete rows or columns until the
resulting r x r matrix has a nonzero
determinant. What is the rank of the above
matrix? If the above matrix had been:
1 9 5
A 3 7 8
4 16 13
note |A|=0. Thus, to determine the rank, we
delete the last row and column leaving
1 9
A1 7 27 20.
A1
3 7
The rank of a matrix A remains unchanged by
any of the following operations, called
elementary transformations:
◦ The interchange of two rows (or columns) of A.
◦ The multiplication of a row (or column) of A by a
nonzero scalar.
◦ The addition of a scalar multiple of a row (or
column) of A to another row (or column) of A.
An m x 1 vector p is said to be a normalized
vector or a unit vector if p’p=1. The m x 1
vectors p1, p2,…pn where n is less than or
equal to m are said to be orthogonal if
pi’pj=0 for all i not equal to j. If a group of n
orthogonal vectors are also normalized, the
vectors are said to be orthonormal. An m x
m matrix consisting of orthonormal vectors is
said to be orthogonal. It then follows:
P' P I
It is possible to show that the determinant of
an orthogonal matrix is either 1 or –1.
In general, the a quadratic form of a matrix
can be written as:
m
m
x' Ay xi y j aij
i 1 j 1
We are most often interested in the quadratic
form x’Ax.
Every symmetric matrix A can be classified
into one of five categories:
◦ If x’Ax > 0 for all x ≠ 0, the A is positive definite.
◦ If x’Ax ≥ 0 for all x ≠ 0 and x’Ax=0 for some x ≠
0, the A is positive semidefinite.
◦ If x’Ax < 0 for all x ≠ 0 then A is negative definite.
◦ If x’Ax ≤ 0 for all x ≠ 0 and x’Ax=0 for some x ≠
0, the A is negative semidefinite.
◦ If x’Ax>0 for some x and x’Ax<0 for some x, then
A is indefinite.
Definition 2.1. Let S be a collection of m x 1
vectors satisfying the following:
◦ If x1 ε S and x2 ε S, then x1+x2 ε S.
◦ If x ε S and a is a real scalar, the ax ε S.
Then S is called a vector space in mdimensional space. If S is a subset of T,
which is another vector space in mdimensional space, the S is called a vector
subspace of T.
Definition 2.2 Let {x1,…xn} be a set of m x 1
vectors in the vector space S. If each vector
in S can be expressed as a linear combination
of the vectors x1,…xn, then the set {x1,…xn} is
said to span or generate the vector space S,
and {x1,…xn} is called a spanning set of S.
Definition 2.6 The set of m x 1 vectors
{x1,…xn} is said to be a linearly independent if
the only solution to the equation
n
a x
i 1
i i
0
is the zero vector a1=…an=0.
1 0 0 1 9 5
3 1 0 3 7 8
4 0 1 4 16 13
1 9
1
0
9
5
20
0 1
0 0 20 7
20
1
1 0 20 7
0
1 0 37
20
0 1 7
20
0
0 0
This reduction implies that:
1
9 5
37 3 7 7 8
20
20
4
16 13
Or that the third column of the matrix is a
linear combination of the first two.