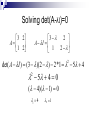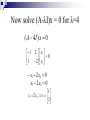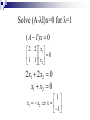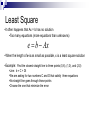Download Slide 1

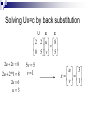
Numerical Linear Algebra
By: David McQuilling
and
Jesus Caban
Solving Linear Equations
2u  2v  8
4u  9v  21
A
x
b
2 2 u   8 
4 9  v   21

   
Gaussian Elimination
Start with the matrix representation of Ax = b by adding the solution vector b
to the matrix A
2 2 8 
4 9 21


Now perform Gaussian elimination by row reductions to transform the matrix Ab
into an upper triangular matrix that contains the simplified equations.
Find the first multiplier by dividing the first entry in the second row by the first
entry in the first row. This will allow you to transform the first entry in the
second row to a zero by a row reduction, thus reducing the system of
equations.
Gaussian Elimination (cont.)
Multiply the first row by the multiplier (4 / 2 = 2) and then subtract that from
the second row to obtain the new reduced equation.
4 9 21
 2(2 2 8)
0 5 5
2 2 8  2 2 8
4 9 21  0 5 5

 

A = LU
The matrix resulting from the Gaussian elimination steps is actually U
concatenated with the new right hand side c.
L is obtained from the multipliers used in the Gaussian elimination steps.
L
U
x
c
1 0 2 2 u  8
2 1 0 5  v   5


   
Solving Ux=c by back substitution
U
x
c
2 2 u  8
0 5  v   5

   
2u  2v  8
2u  2 *1  8
2u  6
u 3
5v  5
v 1
u  3
x  
 v  1
Solution to Ax=b

The solution vector to Ux=c is actually the
solution to the original problem Ax=b.
A
x
b
2 2 u   8 
4 9  v   21

   
2 2 3  8 
4 9 1  21

   
Gaussian algorithm to find LU
After this algorithm completes, the diagonal and upper triangle part
of A contains U while the lower triangle contains L. This algorithm
runs in O(n3) time.
Gram-Schmidt Factorization



Yields the factorization A=QR
Starts with n linearly independent vectors in A
Constructs n orthonormal vectors
A vector x is orthonormal if xTx = 1 and ||x|| = 1
 Any vector is made orthonormal by making it a unit vector in the same
direction, i.e. the length is 1.


 2
a  1 
2
Dividing a vector x by its length (||x||) creates a unit vector in the direction of x
|| a || 22  12  22  3
2 / 3
a / || a || 1 / 3 
2 / 3
Composition of Q and R
 Q is the matrix with n orthonormal column vectors, which were
obtained from the n linearly independent vectors of A.
Orthonormal columns implies that QTQ = I
 R is obtained by multiplying QT on both sides of A = QR
This equation becomes QTA = QTQR = I R = R
R becomes an upper triangular matrix because later q’s are orthogonal to
earlier a’s, i.e. their dot product is zero. This creates zeroes in the entries
below the main diagonal.
Obtaining Q from A

Start with the first column vector from A and use that as your first
vector q1 for Q (have to make it a unit vector before adding it to Q)

To obtain the second vector q2, subtract from the second vector in A,
a2, its projection along the previous qi vectors.


The projection of one vector onto another is defined as (xTy / xTx ) x
where the vector y is being projected onto the vector x.
Once all qi have been found this way, divide them by their lengths so
that they are unit vectors. Now those are the orthonormal vectors
which make up the columns of Q
Obtaining R from QTA


Once Q has been found, simply multiply A by the
transpose of Q to find R
Overall, the Gram-Schimdt algorithm is O(mn2)
for an mxn matrix A.
Eigenvalues and Eigenvectors

Eigenvectors are unique vectors such that when
multiplied by a matrix A, they do not change their
direction only their magnitude, i.e. Ax=λx

Eigenvalues are the scalar multiples of the eigenvectors,
i.e. the λ’s
Solving for eigenvalues of A



Solving for the eigenvalues involves solving det(A–λI)=0
where det(A) is the determinant of the matrix A
For a 2x2 matrix the determinant is a quadratic equation,
for larger matrices the equation increases in complexity
so lets solve a 2x2
Some interesting properties of eigenvalues are that the
product of them is equal to the det(A) and the sum of
them is equal to the trace of A which is the sum of the
entries on the main diagonal of A
Solving det(A-λI)=0
3  
A  I  
 1
3 2
A

1
2


2 
2   
det( A  I )  (3   )(2   )  2 *1    5  4
2
  5  4  0
2
(  4)(  1)  0
1  4
2  1
Solving for the eigenvectors


Once you have the eigenvalues, λ’s, you can solve for
the eigenvectors by solving (A-λI)x=0 for each λi
In our example we have two λ’s, so we need to solve for
two eigenvectors.
Now solve (A-λI)x = 0 for λ=4
( A  4I ) x  0
 1 2   x1 
 1  2  x   0

 2 
 x1  2x2  0
x1  2 x2  0
1 
x1  2 x2  x   
 2
Solve (A-λI)x=0 for λ=1
( A  I )x  0
2 2  x1 
1 1  x   0

 2 
2 x1  2 x2  0
x1  x2  0
1
x1   x2  x   
 1
Positive definite matrices

Positive definite:
 all eigenvalues are positive
 All pivots are positive
 xTAx > 0 is positive except
at x=0

Applications
 Ellipse: find the axes of the
a tilted ellipse
ax  2bxy  cy  1
2
Cholesky Factorization
•Cholesky factorization factors an N*N , symmetric, positive-definite
matrix into the product of a lower triangular matrix and its transpose.
•A = LLT
Least Square
•It often happens that Ax = b has no solution
•Too many equations (more equations than unknowns)
e  b  Ax
•When the length of e is as small as possible, x is a least square solution
•Example: Find the closest straight line to three points (0,6), (1,0), and (2,0)
•Line: b = C + Dt
•We are asking for two numbers C and D that satisfy three equations
•No straight line goes through those points
•Choose the one that minimize the error
Matrix Multiplication
Matrix Multiplication

Matrix multiplication is commonly used in






graph theory
numerical algorithms
computer graphics
signal processing
Multiplication of large matrices requires a lot of
computation time as its complexity is O(n3), where n is
the dimension of the matrix
Most parallel matrix multiplication algorithms use matrix
decomposition based on the number of processors
available
Matrix Multiplication
1 2 3


1 2 3 4  4 5 6   70 80 90 
5 6 7 8  7 8 9   158 184 210






10 11 12
Example (a11):
1
 
4
a11  1 2 3 4   1*1 2 * 4 3 * 7  4 *10  70
7
 
10 
 
Sequential Matrix Multiplication

The product C of the two matrices A and B is
defined by
n 1
cij   a ik  bkj
k 0
aij, bij, and cij is the element in ith row and jth column of
the matrix A, B, and C respectively.
Strassen’s Algorithm

The Strassen’s algorithm is a sequential
algorithm reduced the complexity of matrix
multiplication algorithm to O(n2.81).

In this algorithm, n  n matrix is divided into 4
n/2  n/2 sub-matrices and multiplication is done
recursively by multiplying n/2  n/2 matrices.
Parallel Matrix Partitioning



Parallel computers can be used to process large
matrices.
In order to process a matrix in parallel, it is necessary to
partition the matrix so that the different partitions can be
mapped to different processors.
Partitions:




Block row-wise/column-wise striping
Cyclic row-wise/colum-wise striping
Block checkerboard striping
Cyclic checkerboard
Striped Partitioning

Matrix is divided into groups of complete rows or
columns, and each processor is assigned one such
group.

Striped Partitioning
 Block-Striped: each processor is assigned
contiguous rows or columns
 Cyclic-Striped: is when rows or columns are
sequentially assigned to processors in a
wraparound manner.
Block Stripping
From: http://www.iitk.ac.in/cc/param/tpday21.html
Checkerboard Partition


The matrix is divided into smaller square or
rectangular blocks or sub-matrices that are
distributed among processors
Checkerboard Partitioning
 Block-Checkerboard:
partitioning splits both the
rows and the columns of the matrix, so no processor
is assigned any complete row or column .
 Cyclic-Checkerboard: when it wraparound.
Checkerboard Partitioning
From: http://www.iitk.ac.in/cc/param/tpday21.html
Parallel Matrix-Vector Product



Algorithm:
 For each processor I
 Broadcast X(i)
 Compute A(i)*x
A(i) refers to the n by n/p block row that processor i owns
Algorithm uses the formula
Y(i) = Y(i) + A(i)*X = Y(i) + Sj A(i)*X(j)
Parallel Matrix Multiplication

Algorithms:
 systolic
algorithm
 Cannon's algorithm
 Fox and Otto's algorithm
 PUMMA (Parallel Universal Matrix Multiplication)
 SUMMA (Scalable Universal Matrix Multiplication)
 DIMMA (Distribution Independent Matrix
Multiplication)
Systolic Communication

Communication design
where the data exchange
and communication
occurs between the
nearest-neighbors.
From: http://www-unix.mcs.anl.gov
Matrix Decomposition


To implement the matrix multiplication, the A and
B matrices are decomposed into several submatrices.
Four methods of matrix decomposition and
distribution:
 one-dimensional decomposition
 two-dimensional
 square decomposition
 general decomposition
 scattered decomposition.
One-dimensional Decomposition


The
matrix
is
horizontally
decomposed.
The ith processor
holds ith Asub and Bsub and
communicates them to two neighbor
processors, i.e., to the (i-1)th and
(i+1)th processors.
The first and last processor
communicate with each other as in a
ring topology.
p0 p1 p2 p3 p4 p5 p6 p7
Two-Dimensional Decomposition

Square decomposition: The twodimensional square decomposition
Matrix is decomposed into square
processor template.

General decomposition: General
Two-Dimensional Decomposition
allow having 2*3, 4*3, etc.
configurations.
Two-Dimensional Decomposition

Scattered decomposition: the
matrix is divided into several sets
of blocks. Each set of blocks
contains as many elements as
the number of processors, and
every element in a set of blocks is
scattered according to the twodimensional processor templates.
Applications
Computer Graphics

In computer graphics all the transformation are
represented as matrices and a set of transformations as
a matrix multiplication.
X Rotation

Transformations:
 Rotation
 Translation
 Scaling
 Shearing
© Pixar
2D/3D Mesh
•Laplacian matrix L(G) of the graph G
•If you take the eigenvalues and
eigenvectors of L(G), you can get
interesting properties as vibration of
the graph.
From: http://www.cc.gatech.edu/
Computer Vision
In computer vision we can calibrate a camera to determine the relationship
between what appears on the image (or retinal) plane and where it is
located in the 3D world by using and representing the parameters as
matrices and vectors.
Software for Numerical
Linear Algebra
LAPACK

LAPACK: Routines for solving systems of
simultaneous linear equations, least-squares
solutions of linear systems of equations,
eigenvalue problems, and singular value
problems.

Link:
http://www.netlib.org/lapack/
LINPACK


LINPACK is a collection of Fortran subroutines
that analyze and solve linear equations and
linear least-squares problems. The package
solves linear systems whose matrices are
general, banded, symmetric indefinite,
symmetric positive definite, triangular, and tridiagonal square.
Link:
http://www.netlib.org/linpack/
ATLAS

ATLAS (Automatically Tuned Linear Algebra
Software) provides portable performance and
highly optimized Linear Algebra kernels for
arbitrary cache-based architectures.

Link:
https://sourceforge.net/projects/math-atlas/
MathWorks

MATLAB: provide
engineers, scientists,
mathematicians, and
educators with an
environment for technical
computing applications
NAG

NAG Numerical Library:
solve complex problems in
areas such as research,
engineering, life and earth
sciences, financial
analysis and data mining .
NMath Matrix

NMath Matrix is an advanced matrix manipulation
library. Full-featured structured sparse matrix
classes, including triangular, symmetric, Hermitian,
banded, tridiagonal, symmetric banded, and
Hermitian banded.