Download 3.1 Extrema on an Interval

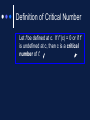
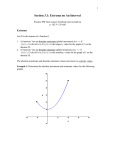
Calculus 5.1:
Extrema on an Interval
Using derivatives to analyze
extrema of a function.
Definition of Extrema
The minimum and maximum of a function on
an interval are called the extreme values, or
extrema, of the function on the interval.
 Extrema can occur at interior points or
endpoints of an interval.

The Extreme Value Theorem
If f is continuous on a closed interval
[a,b], then f has both a minimum and
a maximum on the interval.
(This theorem is an example of an existence theorem because
it tells of the existence of minimum and maximum values,
but does not show how to find these values.)
Relative Extrema



The relative maximum and relative minimum
on a graph are the hills and valleys of the
graph.
If the hill (or valley) is smooth and rounded,
the graph has a horizontal tangent at this
point and the derivative is zero here.
If the hill (or valley) is sharp and peaked,
the function is not differentiable at this point
and the derivative is undefined here.
Example 1
Definition of Critical Number
Let f be defined at c. If f´(c) = 0 or if f´
is undefined at c, then c is a critical
number of f.
Theorem 5.2
The relative extrema of a function
occur only at the critical numbers of
the function.
Knowing this, you can use the following
guidelines to find extrema on a closed
interval.
Guidelines for Finding
Extrema on a Closed
Interval
To find the extrema of a continuous
function on a closed interval [a,b], use the
following steps.
1.
2.
3.
4.
Find the critical numbers of f in (a,b).
Evaluate f at each critical number in (a,b).
Evaluate f at each end point of [a,b].
The least of these values is the minimum.
The greatest is the maximum.
Example 2
Locate the absolute extrema of the function
on
the
interval
[-2,3].
2
f (x)  1 x
Example 3
assignment

Page 319: 1-25 odds, 45