* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 3.1 Extrema on an Interval
Survey
Document related concepts
Transcript
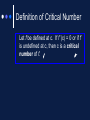
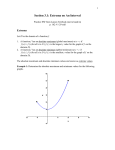
Calculus 5.1: Extrema on an Interval Using derivatives to analyze extrema of a function. Definition of Extrema The minimum and maximum of a function on an interval are called the extreme values, or extrema, of the function on the interval. Extrema can occur at interior points or endpoints of an interval. The Extreme Value Theorem If f is continuous on a closed interval [a,b], then f has both a minimum and a maximum on the interval. (This theorem is an example of an existence theorem because it tells of the existence of minimum and maximum values, but does not show how to find these values.) Relative Extrema The relative maximum and relative minimum on a graph are the hills and valleys of the graph. If the hill (or valley) is smooth and rounded, the graph has a horizontal tangent at this point and the derivative is zero here. If the hill (or valley) is sharp and peaked, the function is not differentiable at this point and the derivative is undefined here. Example 1 Definition of Critical Number Let f be defined at c. If f´(c) = 0 or if f´ is undefined at c, then c is a critical number of f. Theorem 5.2 The relative extrema of a function occur only at the critical numbers of the function. Knowing this, you can use the following guidelines to find extrema on a closed interval. Guidelines for Finding Extrema on a Closed Interval To find the extrema of a continuous function on a closed interval [a,b], use the following steps. 1. 2. 3. 4. Find the critical numbers of f in (a,b). Evaluate f at each critical number in (a,b). Evaluate f at each end point of [a,b]. The least of these values is the minimum. The greatest is the maximum. Example 2 Locate the absolute extrema of the function on the interval [-2,3]. 2 f (x) 1 x Example 3 assignment Page 319: 1-25 odds, 45