Download X - Mrs Michele Murphy Carlisle Math Students

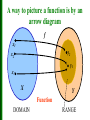
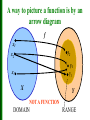
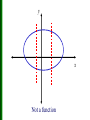
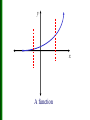
Functions and
Their Properties
Section 1.2
Day 1
Functions
A real-valued function f is a rule that assigns to
each real number x in a set X of numbers, a unique
real number y in a second set Y of numbers.
The set X of all input values is called the domain
of the function f and the second set Y of all output
values is called the range of f.
Functions
To indicate that y comes from the function
acting on x, we use function notation
y = f (x).
f (x) is read “f of x.”
The x is the independent variable and y is the
dependent variable.
A way to picture a function is by an
arrow diagram
f
x1
y2
x2
y1
x3
X
Y
Function
DOMAIN
RANGE
A way to picture a function is by an
arrow diagram
f
x1
y2
x2
y1
y3
x3
X
Y
NOT A FUNCTION
DOMAIN
RANGE
Defining a Function
Does the formula y = x2 define y as a
function of x?
Yes, y is a function of x because we can
rewrite it as
y = f(x) so f(x) = x2
Algebraically Defined Function
Is a function represented by a formula? It has
the format y = f (x) = “expression in x”
Example: f ( x)  3x  2 is a function.
2
f (5)  3(5) 2  2  77
Substitute 5 for x
Graph of a Function
Vertical Line Test: The graph of a function can be
crossed at most once by any vertical line.
Function
Not a Function
It is crossed
more than
once.
y
x
Not a function
y
x
A function
Note on Domains
The domain of a function is not always specified
explicitly.
Unless we are dealing with a model (like volume)
that necessitates a restricted domain, we will
assume that the domain of a function defined by
an algebraic expression is the same as the domain
of the algebraic expression , the implied domain.
For models, we will use a domain that fits the
situation, the relevant domain.
Find the domain of the following functions:
A)
15
B) g ( x ) 
x3
(-∞, ∞)
Domain is all real numbers but
(-∞, 3) U (3, ∞)
x3
C)
Square root is real only for nonnegative numbers.
Domain
Find the domain of each of these functions
a. f ( x)  x  3
b.
x
f ( x) 
x 5
3 2
s , where A( s ) is the area of an equilatera l triangle
c. A( s) 
4
with sides of length s
Support Graphically
f ( x)  x  3
x
f ( x) 
x 5
Range
Find the range of the function
2
f ( x) 
x
Continuity
• We can introduce another characteristic of functions  that of
continuity. We can understand continuity in several ways:
• (1) a continuous process is one that takes place gradually, smoothly,
without interruptions or abrupt changes
• (2) a function is continuous if you can take your pencil and can trace
over the graph with one uninterrupted motion
• Continuous at x = a if
lim f ( x)  f (a)
xa
• Discontinuous at x = a if it is not continuous at x = a
Types of Discontinuities
• (I) Jump Discontinuities:
 x  3, x  1
• ex f ( x)  
2
1

x
, x 1

• We notice our function values
"jump" from 4 to 0
Types of Discontinuities
• (II) Infinite Discontinuities
• ex.
 1

f ( x)   x 2 ; x  0

1; x  0
Types of Discontinuities
• (III) Removable Discontinuities
 x2  x  2
• Ex f ( x)   x  2 ; x  2

1; x  2

• “Hole” in the graph
Continuity
Increasing and Decreasing Functions
Describe the increasing and decreasing behavior.
The function is
decreasing over the
entire real line.
Increasing and Decreasing Functions
Describe the increasing and decreasing behavior.
The function is
decreasing on the
interval  , 1

increasing on the
interval  1, 0
decreasing on the
interval 0, 1
increasing on the
interval 1,  

Increasing and Decreasing Functions
Describe the increasing and decreasing behavior.
The function is
increasing on the
interval  4,  1


constant on the
interval  1,

2
decreasing on the
interval
2, 5
 
Boundedness
BOUNDEDNESS
Example
Identify each of these functions as bounded below,
bounded above, or bounded.
x
1. f(x) = 3x2 – 4
2. g ( x ) 
2
1 x