Download Probability - Andrew.cmu.edu

Lecture 5. Basic Probability
David R. Merrell
90-786 Intermediate Empirical Methods
For Public Policy and Management
I think that the team that wins game five
will win the series...Unless we lose game
five.
-- Charles Barkley
Regularity: Empirical Rule
XS
contains 68% of data
X  2S
contains 95% of data
X  3S
contains 99.9% of
data
How to Verify?



Try Monte Carlo simulations
Easy to use Minitab
Let’s do that!
Terminology




Probability trial: a process giving
observations with uncertain values
Repeated probability trials:
independently repeated under the same
conditions
Outcome: a most basic happening
Event: set of outcomes
Assignment of Probabilities
1. Symmetry--Classical
2. Relative Frequency
3. Betting Odds--Subjective
Classical Approach




Elementary outcomes are equally likely
Probability is defined to be the
proportion of times that an event can
theoretically be expected to occur
Used in standard games of chance
We can determine the probability of an
event occurring without any experiments
or trials ever taking place
Example 1 - Rolling a die



Experiment: Roll a die
Sample space: S = {1, 2, 3, 4, 5, 6}
Number of possible outcomes: 6



P(4) = 1/6
P(even) = 3/6
P(number < 3) = 2/6
Example 2 - Flipping a coin



Experiment: Flip 2 coins
Sample space: S = {HH, TH, HT, TT}
Number of possible outcomes: 4


P(both heads) = 1/4
P(at least one tail) = 3/4
Example 3 - Drawing a card


Experiment: Draw a card from a deck
of 52
Number of possible outcomes: 52



P(ace) = 4/52
P(diamond) = 13/52
P(red and ace) = 2/52
Relative Frequency Approach


Used when classical approach is not
applicable and repeated probability
trials are possible
Probability is the proportion of times an
event is observed to occur in a large
number of trials
Example 4--Relative Frequencies



In 1985, 22.9% of whites were below
the poverty level
In 1977, the percent urban in Iraq was
64.
In 1984, the divorce rate in Maine was
3.6 per 1000 population. (Problems
here!)
Law of Large Numbers
average
0.0
-0.5
-1.0
Index
100
200
300
“Law of Small Numbers”

Toss a coin 1000 times and it will show
up heads 500 times???
“Law of Averages”

“I’ve lost money every time I bought a
stock...I’m due!”
Subjective Approach


Used when repeated probability trials
are not feasible.
Probability is subjective--an educated
guess, a personal assessment
Well-Calibrated Probability Forecaster



Link subjective probability to repeated
probability trials
P(MSFT goes up tomorrow) = .55
Does it go up 55% of the time?
Example 5--Subjective Probability


What is the probability that the
Pittsburgh Steelers will win next week?
What is the probability that Al Gore will
be elected president in the year 2000?
Odds vs. Probabilities

Odds are a restatement of probability



If the probability that an event will occur is 3/5, then the odds in
favor of the event occurring are 3:2
Odds against an event occurring are the reverse
of odds in favor of occurring. In this case 2:3.
To calculate the probability, given the odds 1:3
1
1
1+3
4
probability is 1/4
Odds
Odds of a:b in favor of an event A
A Occurs
A Does Not
Bet in Favor
Bet Against
b
-b
-a
a
Probability Notation





P(A) - probability that event A occurs
P(A’) - probability that event A will not occur (A’ is
the complement of A)
P(A B) - probability that A will occur or B will
occur or both (Union of A and B)
P(A  B) - probability that A and B will occur
simultaneously (Joint probability of A and B)
P(A | B) - probability of A, given that B is known
to have occurred. (Conditional probability)
Probability Axioms
1. P(A) > 0
2. P(S) = 1
3. Ai mutually exclusive,
P (  Ai ) 
 P( A )
i
Addition Law for Probability
P(A or B) = P(A) + P(B) - P(A and B)
Example: A left engine functions
B right engine functions
“Proof by Paint”
P( A or B)  P( A  B)  P( A)  P( B)  P( A  B)
A
B
1
1
0
“paint and scrape”
A
B
1
22
1
If Mutually Exclusive ...
P(A or B) = P(A) + P(B)
Note simplification of Addition Rule
If Independent ...
P(A and B) = P(A)P(B)
Note simplification of Multiplication Rule
Some Connections ...
Logic
and
or
Set
Arithmetic
 x

+
Simplification
independence
mutually exclusive
Note: independence is NOT mutual exclusivity
Multiplication Law for Probability

P(A and B) = P(A
P(A|B)P(B)
B) = P(A)P(B|A) =
Example
Sell cocaine and go to jail
A
B
Example 6--Probability Calculations
P(adult male is a Democrat) = 0.6,
P(belongs to a labor union) = 0.5
P(Democrat and labor union) = 0.35,
Find the probability that an adult male chosen at
random:
 is a Democrat or belongs to a labor union
 does not belong to a labor union
 is a Democrat given that he belongs to a labor
union
Conditional Probability
Events A, B
P(A and B) = P(B |A)P(A) = P(A|B)P(B)
Definition:
P( A B)
P ( B| A) 
P ( A)
Example 7--Conditional Probability
  {1, 2 ,  , 10}
A  odd number = {1, 3, 9}
B = prime number = {2, 3, 5, 7}
P(A  B)
P{3,5,7}
3
P(A|B) =


P(B)
P{2 ,3,5,7} 4
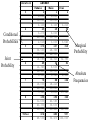
Contingency Table



Help determine probabilities when we
have two variables
Joint and conditional probabilities are in
the cells
Marginal probabilities are on the
“margins” of the table
Educational Achievement:
Coding of Ordinal Variable








1 if grade 4 or less
2 if grades 5-7
3 if grade 8
4 if high school incomplete (9-11)
5 if high school graduate (12)
6 if technical, trade, or business after high
school
7 if college/ university incomplete
8 if college/university graduate or more
Educational Achievement Table
Education
Female
No.
Male
%
No.
Total
%
No.
%
3
1
0.21%
1
0.21%
2
0.21%
4
5
6
7
8
25
173
49
76
150
5.27%
36.50%
10.34%
16.03%
31.65%
29
137
32
88
196
6.00%
28.36%
6.63%
18.22%
40.58%
54
310
81
164
346
5.64%
32.39%
8.46%
17.14%
36.15%
Total
474
100.00%
483
100.00%
957
100.00%
Education
Gender
Female
3
4
5
6
7
8
Total
1
0.21%
50.00%
0.10%
25
5.27%
46.30%
2.61%
173
36.50%
55.81%
18.08%
49
10.34%
60.49%
5.12%
76
16.03%
46.34%
7.94%
150
31.65%
43.35%
15.67%
474
49.53%
Male
1
0.21%
50.00%
0.10%
29
6.00%
53.70%
3.03%
137
28.36%
44.19%
14.32%
32
6.63%
39.51%
3.34%
88
18.22%
53.66%
9.20%
196
40.58%
56.65%
20.48%
483
50.47%
Total
2
0.21%
54
5.64%
310
32.39%
81
8.46%Count--Absolute
164
Frequency
17.14%
346
36.15%
957
100.00%
Education
Gender
Female
3
4
5
Joint
Probability
6
7
8
Total
1
0.21%
50.00%
0.10%
25
5.27%
46.30%
2.61%
173
36.50%
55.81%
18.08%
49
10.34%
60.49%
5.12%
76
16.03%
46.34%
7.94%
150
31.65%
43.35%
15.67%
474
49.53%
Male
1
0.21%
50.00%
0.10%
29
6.00%
53.70%
3.03%
137
28.36%
44.19%
14.32%
32
6.63%
39.51%
3.34%
88
18.22%
53.66%
9.20%
196
40.58%
56.65%
20.48%
483
50.47%
Total
2
0.21%
54
5.64%
310
32.39%
81
8.46%
164
17.14%
346
36.15%
957
100.00%
Education
Gender
Female
3
4
5
6
7
8
Total
1
0.21%
50.00%
0.10%
25
5.27%
46.30%
2.61%
173
36.50%
55.81%
18.08%
49
10.34%
60.49%
5.12%
76
16.03%
46.34%
7.94%
150
31.65%
43.35%
15.67%
474
49.53%
Male
1
0.21%
50.00%
0.10%
29
6.00%
53.70%
3.03%
137
28.36%
44.19%
14.32%
32
6.63%
39.51%
3.34%
88
18.22%
53.66%
9.20%
196
40.58%
56.65%
20.48%
483
50.47%
Total
2
0.21%
54
5.64%
310
32.39%
81
8.46%
164
17.14%
346
36.15%
957
100.00%
Marginal
Probability
Education
Gender
Female
3
Conditional
Probabilities:
4
P(Ed =4|F)
P(F|Ed=4)
5
6
7
8
Total
1
0.21%
50.00%
0.10%
25
5.27%
46.30%
2.61%
173
36.50%
55.81%
18.08%
49
10.34%
60.49%
5.12%
76
16.03%
46.34%
7.94%
150
31.65%
43.35%
15.67%
474
49.53%
Male
1
0.21%
50.00%
0.10%
29
6.00%
53.70%
3.03%
137
28.36%
44.19%
14.32%
32
6.63%
39.51%
3.34%
88
18.22%
53.66%
9.20%
196
40.58%
56.65%
20.48%
483
50.47%
Total
2
0.21%
54
5.64%
310
32.39%
81
8.46%
164
17.14%
346
36.15%
957
100.00%
Education
Gender
Female
3
4
Conditional
Probabilities
Joint
Probability
5
6
7
8
Total
1
0.21%
50.00%
0.10%
25
5.27%
46.30%
2.61%
173
36.50%
55.81%
18.08%
49
10.34%
60.49%
5.12%
76
16.03%
46.34%
7.94%
150
31.65%
43.35%
15.67%
474
49.53%
Male
1
0.21%
50.00%
0.10%
29
6.00%
53.70%
3.03%
137
28.36%
44.19%
14.32%
32
6.63%
39.51%
3.34%
88
18.22%
53.66%
9.20%
196
40.58%
56.65%
20.48%
483
50.47%
Total
2
0.21%
54
5.64%
310
Marginal
Probability
32.39%
81
8.46%
164
17.14%
346
36.15%
957
100.00%
Absolute
Frequencies
Example 8--More Probability
Calculations
Find the probability that the individual:






is a high school graduate
is female
is male or has incomplete high school
is female and did not complete college
graduated from college given that he is a
male
is male given that he graduated from
college
Next Time ...



Bayes Rule
Total Probability Rule
Applications