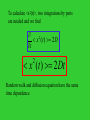Download Simulation of Random Walk

Simulation of Random Walk
• How do we investigate this numerically?
• Choose the step length to be a=1
• Use a computer to generate random numbers ri
uniformly in the range [0,1]
• if ri  p then increase x by 1 => x=x+1
• otherwise decrease x by 1 => x=x-1
• calculate total x(N) after N steps
• any value in the range -N< x < +N is possible
• calculate <x(N)> and <x2(N)>-<x(N)>2 by
repeated trials
Two trials with N=5000 steps
Monte Carlo Simulation
of 1-d Random Walk
Random Walk in 2 dimensions
• Let the walker start at the origin and choose
each of the four directions with equal
probability (p=1/4)
• at each step choose random number ri
• if ri  .25
x=x+1
• if .25< ri  .5 x=x-1
• if .5 < ri  .75 y=y+1
• if .75 < ri  1 y=y-1
Random walk in 2 dimensions
x  x  g
b

p  q  1/ 4
by  y  g

 x  y  0
N
2
  4 pqN 
4
2
p( x , N )  p( x ) 
1
2
2
2 2
e
2
p( y , N )  p( y ) 
1
2
2
e
p(r ,  )rdrd  p( x ) p( y )dxdy
2
1
p( r ,  ) 
e
2
2
r
 2
2
2 2
r
p( r )  e
N
r2

2N
Random Walk
 x  y  0
N
N
 x  y  (1  1  0  0) 
4
2
2
2
2
 r  x    y  N
2
2
rrms  r    
2
1/ 2
N
Walk2d
simulation
Monte Carlo Method
• Perform many trials and calculate the
average of any quantity <A>
• calculate the variance [<A2>-<A>2]
• error in <A>   [(<A2>-<A>2)/ntrial]1/2
Random Walks and
the Diffusion Equation
P( x , t )
 P( x , t )
D
2
t
x
2
• This is the diffusion equation for the probability of
finding a particle at position x at time t
• what is the dependence of <x(t)> and <x2(t)> on t?
• the average of any function f(x) is
z

 f ( x, t ) 
f ( x) P( x, t )dx

z

 x(t ) 
x P( x, t )dx

Multiply the diffusion equation on both sides by x and
integrate over x
z

z

P( x, t )
 2 P( x , t )
x
dx  D x
dx
2
t
x


Left side becomes

x
t
P ( x  , t )  0
Right side is zero since
Hence   x  0   x  0
t
P ( x , t )
x
0
x 
To calculate <x2(t)>, two integrations by parts
are needed and we find

2
 x (t )  2 D
t
 x (t )  2 Dt
2
Random walk and diffusion equation have the same
time dependence
Monte Carlo Methods
Consider the problem of integration in one dimension
b
F =  f(x) dx
a
The classical methods of numerical integration are based
on the geometrical interpretation of the integral as the
area under the curve of f(x) from x=a to x=b
Integration
• For some choices of f(x) the integral can be
evaluated analytically eg. cos(x)
• classical methods of numerical integration are based
on the geometrical interpretation of the integral as
the ‘area’ under the curve of the function
f(x) from x=a to x=b
• divide the x-axis into n equal intervals of width x,
where
x=(b-a)/n
Rectangular Approximation
cos(x)
an estimate
of the area is
n 1
Fn   f ( xi ) x ; xi  a  ix
i 0
f(x)=cos(x)
• Consider f(x)= cos(x) with a=0 and b=/2
z
 /2
F
cos( x)dx  sin( x) 0
0
• compare with numerical results
• error decreases as 1/n
 /2
1
error decreases as 1/n
Trapezoidal Rule
• A better approximation to the area is given
by the trapezoidal rule
• rather than using f(xi)x we use the
average of f(x) at the beginning and end of
the interval (1/2)[f(xi+1)+f(xi)] x
• error decreases as 1/n2
L
O
1
1
F  Mf ( x )   f ( x )  f ( x ) P
x
2
N2
Q
n 1
n
0
i
i 1
n
Simpson’s Rule
• A more accurate method is to use a
quadratic or parabolic interpolation
procedure
• Simpson’s rule error decreases as 1/n4
• adequate for well behaved functions
• But a function such as f(x)= x-1/3 is poorly
behaved at x=0 and would present problems
Simpson’s Rule
Simpson’s
Rule
chapter 11
integtrap
1
Fn  [ f ( x0 )  4 f ( x1 )  2 f ( x2 )  4 f ( x3 ) ...
3
 2 f ( xn  2 )  4 f ( xn 1 )  f ( xn )]x
Can we evaluate this using random
numbers?
• Consider a rectangle of height H, width
(b-a), and area A= H x (b-a) such that
f(x) lies within the rectangle
hit or miss algorithm
• Compute ‘n’ pairs of random numbers
•
(xi , yi)
•
with a xi b and 0yi H
• The fraction of the points that satisfy
yi  f( xi) is an estimate of the ratio of the
integral to the area of the rectangle
•
Fn = A (ns / n)
• where ns is the number of "splashes" below
the curve and ‘n’ is the number of trials.
Eg.
f(x) = 4 sqrt( 1 – x2) on the interval 0  x  1
F(exact) =  = 3.14159
n
50000.
100000.
150000.
200000.
250000.
300000.
350000.
400000.
450000.
500000.
550000.
600000.
650000.
700000.
750000.
800000.
850000.
900000.
950000.
1000000.
Fn
3.13968
3.14356
3.14237
3.14144
3.13952
3.13959
3.13782
3.13821
3.13862
3.13882
3.13917
3.13831
3.13941
3.13977
3.14051
3.14103
3.14103
3.14103
3.14154
3.14244
F-Fn
0.00191
0.00197
0.00078
0.00015
0.00207
0.00200
0.00377
0.00338
0.00297
0.00277
0.00242
0.00328
0.00218
0.00182
0.00108
0.00057
0.00056
0.00056
0.00005
0.00085
Hit
Note: all points have equal probability and points above f(x)
have zero contribution to Fn but increase the fluctuations
Sample mean approach
• Choose the xi at random and sample
the value of f(xi)
• Mean-value theorem of calculus:
•
F = (b-a) < f >
• For n trials, Fn = (b-a)(1/n) i=1,nf(xi)
• where the xi are distributed uniformly on
the interval a  xi b
f(x) = 4 sqrt( 1. – x2) [0,1]
• The exact value of the integral is
•
 = 3.14159
n
1000.
10000.
Fn
F-Fn
n
3.17026
3.14968
0.02867
0.00809
0.86768
0.88455
Note that the standard deviation of the integrand is roughly
constant but that the error decreases with n as ~ 1/n1/2
c
Program Sampling
n=10000
h=1.
a=0.
b=1.
sum=0.
sum2=0.
m=2
do 4 i=1,n
x=a+b*r250(idum)
f=4.*sqrt(1.-x*x)
sum=sum+f
sum2=sum2+f*f
sig2=sum2/i -(sum/i)*(sum/i)
sig=sqrt(sig2)
if((i-(i/10**m)*10**m).eq.0) then
write(6,10)1.*i,sum/i,abs(3.14159-sum/i),sig
m=m+1
else
continue
end if
10 format(1x,f10.0,3x,f10.5,3x,f10.5,3x,f10.5)
4
continue
stop
end
Now fix the number of trials and repeat with a
different set of random numbers
Run
n
1
2
3
4
5
6
7
8
9
10
10000.
10000.
10000.
10000.
10000.
10000.
10000.
10000.
10000.
10000.
Fn
3.14968
3.13242
3.13669
3.15016
3.11856
3.14716
3.13996
3.13696
3.14782
3.14860
F-Fn
n
0.00809
0.00917
0.00490
0.00857
0.02303
0.00557
0.00163
0.00463
0.00623
0.00701
0.88455
0.88498
0.89087
0.88916
0.90492
0.88839
0.89368
0.89214
0.89010
0.89147
The mean value is <Fn> = 3.14080
The standard deviation of the means is
 = (<Fn2> - <Fn>2 )1/2 = 9.46813E-03 
Hence,
n/n1/2
F = (b-a)< f >  (b-a) (<f2> - <f>2 )1/2
n1/2
c program sample mean
n=10000
h=1.
a=0.
b=1.
rsum=0.
rsum2=0.
do 5 j=1,10
sum=0.
sum2=0.
do 4 i=1,n
x=a+b*r250(idum)
f=4.*sqrt(1.-x*x)
sum=sum+f
sum2=sum2+f*f
sig2=sum2/i -(sum/i)*(sum/i)
sig=sqrt(sig2)
if((i-(i/n)*n).eq.0) then
write(6,10)j, 1.*i,sum/i,abs(3.14159-sum/i),sig
else
continue
end if
10
format(i5,1x,f10.0,3x,f10.5,3x,f10.5,3x,f10.5)
4
continue
rsum=rsum+sum/n
rsum2=rsum2+(sum/n)**2
5
continue
rsum=rsum/10.
rsum2=rsum2/10.
rsig2=rsum2-rsum**2
rsig=sqrt(rsig2)
write(6,*) rsum,rsig,rsum+rsig,rsum-rsig
stop
end
In general dimension,
F = V < f >  V (<f2> - <f>2 )1/2
n1/2
Multidimensional Integrals
Consider a small atom such as magnesium with 12 electrons
To calculate electronic properties we need to integrate over
all coordinates 3 x 12 = 36 dimensional integral!
With 64 points for each integration, this requires 6436 ~ 1065
evaluations of the integrand => impossible!
Example:
=155/6 = 25.83333
integ10