Download Chapter 1 A Beginning Library of Elementary Functions

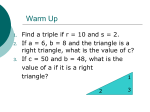
Chapter 1
A Beginning Library of Elementary
Functions
Section 1
Functions
Definition of a function
• A Function is a rule (process or method) that
•
produces a correspondence between two sets of
elements such that to each element in the first
set there corresponds one and only one element
in the second set.
The first set is called the domain (x values) and
the second set is called the range (y values).
Examples
Domain
Range
Domain
Range
-2
-8
-2
4
-1
-1
-1
1
0
0
0
0
1
1
1
2
8
2
Function
Function
Domain
Range
0
0
1
1
-1
4
2
-2
9
3
-3
Not a Function
Vertical Line Test
• An equation defines a function if each
vertical line in the coordinate system
passes through at most one point on the
graph of the equation.
• If any vertical line passes through two or
more points on the graph of an equation,
then the equation does not define a
function.
Examples
Not a Function
Function
Not a Function
Functions Defined by Equations
• If in an equation in two variables, we get
exactly one output (value for the
dependent variable) for each input (value
for the independent variable), then the
equation defines a function.
• If we get more than one output for a
given input, the equation does not define
a function.
Examples
Example 1
4 y  3x  8
 4 y  3x  8
3x  8
 y
4
Function
Example 2
y2  x2  9

y  x 9

y  x 9

2
2
2
2
y   x 9
2
Not a Function
Function Notation
• For any element x in the domain of the
function f, the symbol f(x) represents the
element in the range of f corresponding to
x in the domain of f. If x is an input value,
then f(x) is the corresponding output
value. If x is an element that is not in the
domain of f, then f is not defined at x and
f(x) does not exist.
Function Evaluation
Example 1
Example 2
2
12
g
(
x
)

1

x
f ( x) 
x2
2
g
(

2
)

1

(

2
)
12
12
f (6) 
 3
 1  4  3
62 4
Example 3
h( x )  x  1
h(2)  2  1
 3
Not a Real Number
Domains and Ranges of a Function
• If a function is specified by an equation
and the domain is not indicated, then we
assume that the domain is the set of all
real number replacements of the
independent variable (inputs) that produce
real values for the dependent variable
(outputs). The range is the set of all
outputs corresponding to input values.
Finding the Domain of a Function
• Problems
– Zero in the denominator
– Negative numbers under square roots
• Take values of x that cause problems out
of the domain