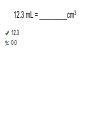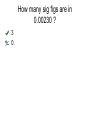* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download scientific notation
Survey
Document related concepts
Transcript
Measuring in Science Metric System Dimensional Analysis Density Scientific Notation Sig Figs Scientific Notation • Numbers in science are often very large or very small. • To avoid confusion, we use scientific notation. • Scientific notation utilizes the numeric digits in a measurement followed by a power of ten. • The numeric digits are expressed as a number between 1 and 10. Multiplying/Dividing with Sci Notation • When multiplying with sci notation, multiply the base numbers and ADD exponents • When dividing with sci notation, divide the base numbers and SUBTRACT the exponents • There are 26,800,000 helium atoms in 1.00 L of helium gas. Express the number in scientific notation. A. B. C. D. 26, 800,000 X 107 2.6800000 X 107 2.68 X 107 None of the above 0.0089. Express the number in scientific notation. A. B. C. D. .0089 X 103 8.9 X 103 8.900 X 103 None of the above Conversion Factors • A conversion factor takes the unit equation and converts it into a ratio. • For example, 2.2 cm= 1 inch, so… • To convert 3 cm to inches, simply set up as follows: 3 cm 1 in 2.2 cm Dimensional Analysis (cont) • To convert 3 inches to cm, simply set up as follows: 3 in 2.2 cm 1 inch If there are 2 googles in 4 blats, 1 google equals _________ blats 2.0 0.1 • The mass of an object is a measure of the amount of matter it posses. • Mass is measured with a balance and is not affected by gravity. • Weight is the force exerted by gravity on an object • Mass and weight are not interchangeable • The SI unit for mass is the kilogram (kg) • 1 kg = 2.20 lb M a s s Volume • Volume is the amount of space • occupied by matter. • The SI unit for volume is the cubic meter (m3) • The metric unit (and the more often used unit) is the liter (L) • There are several instruments for measuring volume • 1 mL = 1 cm3 12.3 mL = _________cm3 12.3 0.0 Metric Conversions • Kilo –Hecto • Deka –M or L or g »Deci » centi » milli 3.50 mg =______g .00350 0.0 Sig Figs • Zeros found at the beginning of a number ARE never significant. • Therefore, 0.5 cm, 0.05 cm, and 0.005 cm all have one significant digit. • Zeros found at the end of a number with no decimal point ARE NOT significant. • Therefore, 50 cm, 500 cm, and 5000 cm all have one significant digit. • All other zeros are significant • Therefore, 50.0 cm, 0.0500 cm, and 501cm all have three significant digits. How many sig figs are in 0.00230 ? 3 0. Finding Density for a Regular Object • 1. – Use the balance to find the mass of the object. Record this value on the "Density Data Chart." • 2. – Use the metric ruler to measure the length, width, height, or diameter of the object. Record the values that apply to your object. • 3. – Compute the volume of the object using the values determined in step 2. Record the volume on the data chart. • 4. – Compute the density of the object by dividing the mass value by the volume value. Record the density on the data chart. • If the volume of an object is 4 mL, and the mass is 2 g, what is the density of the object? (don’t worry about units) .5 0.1 Finding Density for an Irregular Object • 1. – Use the balance to find the mass of the object. Record the value on the "Density Data Chart." • 2. – Pour water into a graduated cylinder up to an easily-read value, such as 50 milliliters and record the number. • 3. – Drop the object into the cylinder and record the new value in millimeters. • 4. – The difference between the two numbers is the object's volume. Remember that 1 milliliter is equal to 1 cubic centimeter. Record the volume on the data chart. • 5. – Compute the density of the object by dividing the mass value by the volume value. Record the density on the data chart.