Download Lesson 2.4 Solving Multiple Equations

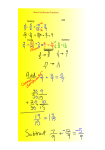
2.4 Solving Multi-Step Equations
Indicators:
PFA7, PFA8, PFA9
Written by ???
Edited by Eddie Judd, Crestwood Middle School
Edited by Dave Wesley, Crestwood Middle School
To Solve: Undo the operations by
working backward.
Ex: x + 9 = 6
5
Ask yourself:
• What is the first thing
we are doing to x?
• The second thing?
Recall the order of
operations as you
answer these questions.
• dividing by 5
• adding 9
To undo these steps, do
the opposite operations
in opposite order.
The DO-UNDO chart
Use a chart as a shortcut to
answering the questions.
DO UNDO
• ÷5
-9
• +9
·5
Follow the steps in the
‘undo’ column to isolate
the variable.
Ex: x + 9 = 6
5
• First subtract 9.
x+9-9=6-9
5
x = -3
5
• Then multiply by 5.
(5) x = -3(5)
5
x = -15
Let’s try another!
Complete the do-undo chart.
DO UNDO
• -2
·3
• ÷3
+2
To solve for d:
• First multiply by 3.
• Then add 2.
Ex: d - 2 = 7
3
(3) d - 2 = 7(3)
3
d - 2 = 21
+2 +2
d = 23
Here’s a tricky one!
Remember to always use the
sign in front of the number.
DO UNDO
• ÷ -7
-3
• +3
· -7
To solve for a:
• First subtract 3.
• Then multiply by -7.
Ex: 3 - a = -2
7
•
3 - a = -2
7
-3
-3
- a = -5
7
• (-7)(- a) = (-5)(-7)
7
a = 35
Try a few on your own.
• 5z + 16 = 51
• 14n - 8 = 34
• 4b + 8 = 10
-2
Example 1
5z + 16 = 51
Example 2
• 14n - 8 = 34
Example 3
•
4b + 8 = 10
-2
The answers:
DO
• ·5
• +16
• z=7
UNDO
- 16
÷5
DO
UNDO
• · 14 +8
• -8
÷ 14
• n=3
DO
• ·4
UNDO
· -2
• +8
• ÷ -2
-8
÷4
• b = -7
Consecutive Numbers
• Consecutive means-- In order/In sequence.
Ex:
1, 2, 3…
10,11,12…
20, 22, 24, 26… (Evens)
51, 53, 55 etc. . . (Odds)
Let’s try one!!!
Find three consecutive integers that have a
sum of 15.
What is this asking?
+
+
=
15
Almost there!
n
+
n+1
+
n+2
=
15
• Since we don’t know what the first number
is, let’s call it “n.”
• The next number would be “1 more than n”
• The next would be “2 more than n”
Let’s complete the problem!
So the problem looks like this:
n + (n + 1) + (n + 2) = 15 Scary Right?!?
Nah!!!
3n + 3 = 15
LIKE TERMS!!! EASY!!!
Solve It!!
3n + 3 = 15
-3 -3
3n = ___
12
___
3
3
n = 4
So if n = 4, (n + 1) = 5 and (n + 2) = 6
Your three consecutive numbers are: 4, 5, and 6
Assignment
Algebra 1
• Pg 95 Problems 11-26 all, 29 and 33-37 odds
• Honors Algebra 1
• Pg 95 Problems 11-23 odd, 25-28 all, 31-37 all
40-42 all