* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Cryptography issues – elliptic curves
Survey
Document related concepts
Transcript
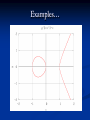
Cryptography issues – elliptic curves Presented by Tom Nykiel What are we going to talk about… What is cryptography ? Why do we need it ? Who uses cryptographic services ? How is it done classically ? Elliptic curves How is it done using elliptic curves ? Summary What is cryptography ? Hiding of meaning of messages Branch of information theory Study of information and especially its transmission from place to place In the past mainly encrypting But now… Why do we need it ? 1. 2. 3. 4. Information protection services nowadays: Integrity Authentication Non-repudiation Confidentiality Who uses cryptographic services ? Banking : ATM, online banking Computer science : securing networks and systems Military : securing confidential information Love letters Much more… How is it done classically ? 1. 2. 3. Symmetric approach – both sides have the same amount of information which is used in encrypting process Fast encoding (O(n)) Exponential time complexity key security Short keys Examples : DES, AES, Blowfish, IDEA, Twofish, Serpent Any problems ? 1. 2. 3. Asymmetric approach : both sides have some information sufficient to encode/decode May be used in establishing a symmetric key Hundreds or thousands time slower than sym. Computationally secure Still good performance Examples: RSA, Diffie-Hellman, El-Gamal, Computationally hard issues - - RSA algorithm Factorization problem : find such prime numbers p and q for a given n that p*q=n Diffie-Hellman Discrete logarithm problem : find x such that g^x mod p = A for given g, p and A Diffie-Hellman scheme Diffie Hellman… Alice and Bob agree to use a prime number p=23 and base g=5. Alice chooses a secret integer a=6, then sends Bob (g^a mod p) 56 mod 23 = 8. Bob chooses a secret integer b=15, then sends Alice (g^b mod p) 515 mod 23 = 19. Alice computes (g^b mod p)^a mod p 196 mod 23 = 2. Bob computes (g^a mod p)^b mod p 815 mod 23 = 2. Modern cryptography Elliptic curves In mathematics, an elliptic curve is an algebraic curve defined by an equation of the form Y^2 = X^3 + aX + b, Examples… Examples… Examples… Modular arithmetic Addition and multiplication Hard problems… For given S find P and Q such that P+Q=S – factorization problem For given G and P find a such that aG=P – discrete logarithm problem Diffie Hellman for EC Time complexity issues 1. 2. 3. 1. Classical approach – Recall the algorithm of multiplying two num. in O(n^2) O(n^1.58) O(n logn loglog n) time A^B = A^(B/2) * A^(B/2) [ *A] Results in polynomial time in number of bits of the exponent b. Apply the same idea to EC kA = 2 * (k/2)*A Key length comparison References Standards for Efficient Cryptography Group http://www.secg.org Tutorial EC http://www.certicom.com RSA labs http://www.rsasecurity.com/rsalabs www.wikipedia.org