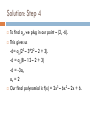Download Finding a Polynomial passing through a point

FINDING A POLYNOMIAL
PASSING THROUGH A POINT
Review: the Linear Factorization
Theorem
If
where n > 1 and an ≠ 0
then
Where c1, c2, … cn are complex numbers
(possibly real and not necessarily distinct)

This theorem lets us generate polynomials with any
zeroes by multiplying their corresponding factors.
Specific Points


If we want to find a polynomial with given zeroes
that passes through a point, we can use basically
the same technique.
We’ll still multiply together all the factors that
correspond to the zeros of the polynomial, but we’ll
also multiply by a constant term (an) that results in
the point we want.
The Technique
1.
2.
3.
4.
Determine all the zeroes you want your polynomial
to have and what multiplicity each should have.
Generate a factor for each zero.
Multiply together all the factors. Multiply by each
one a number of times equal to its multiplicity.
Plug in the point that you want the polynomial to
pass through and determine the value of an.
Example

Find a third degree polynomial with zeroes -1, 1,
and 3 that passes through the point (2, -6).
Solution: Step 1



The first step is to determine all the zeroes and their
multiplicities.
With three zeros, we already have enough factors
to form a third degree polynomial, so all of our
zeros will have multiplicity 1.
The zeroes, again, are -1, 1, and 3.
Solution: Step 2

Since our zeroes are -1, 1, and 3, our three factors
are (x + 1), (x – 1), and (x – 3).
Solution: Step 3





Now, we multiply all the factors together and expand
the product.
This gives us x3 – 3x2 – x + 3.
Our equation, in its current form, is
f(x) = an(x3 – 3x2 – x + 3).
Now we just need to find an.
If we just wanted a polynomial with the given zeroes,
we could choose any value of an (usually 1), but we
need our function to go through a particular point.
Solution: Step 4



To find an, we plug in our point – (2, -6).
This gives us
-6= an(23 – 3*22 – 2 + 3).
-6 = an(8 – 12 – 2 + 3)
-6 = -3an
an = 2
Our final polynomial is f(x) = 2x3 – 6x2 – 2x + 6.
Graph
We can
check our
answer by
checking
whether the
graph of the
function goes
through the
point we
wanted. It
does!