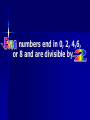Download Divisibility Rule 2

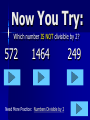
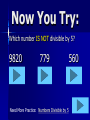
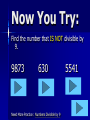
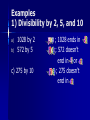
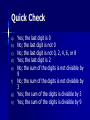
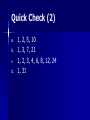
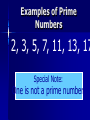
Tuesday, September 21
Agenda
① Fill in planner
①
②
②
③
④
⑤
Practice 4-1
Enrichment 4-1 (E.C.)
Bell Work
Go over Ch. 1 Test
Notetaking WS
(Divisibility and Factors)
Group Work
Bell Work
Objective: Students will
be able to identify
factors and use
divisibility rules
“Divisible BY”
What does it mean?
“Divisible by” means:
If you divide one number by another, the result is
a whole number WITHOUT a remainder.
Examples:
12 ÷ 6 = 2 No remainder
15 ÷ 5 = 3 No remainder
Divisibility Rule 2
A number is divisible by 2 if it
ends in 0, 2, 4, 6, or 8.
Examples:
78
3470
Now You Try:
Which number IS NOT divisible by 2?
572
1464
Need More Practice: Numbers Divisible by 2
249
WONDERFUL
It ends in a 0,
2, 4, 6, or 8.
Divisibility Rule 5
A number is divisible by 5 if it ends
in 0 or 5.
Examples:
615
1480
ends in a 5
ends on a 0
Now You Try:
Which number IS NOT divisible by 5?
9820
779
Need More Practice: Numbers Divisible by 5
560
The number ends in a
zero or a five.
Divisibility Rule 10
A number is divisible by 10 if it ends in 0
Examples:
1320 1320 ÷ 10 = 132
100
100 ÷ 10 =10
Now You Try:
Which number IS NOT divisible by 10?
560
4101
180
WONDERFUL
The last digit is 0.
numbers end in 0, 2, 4,6,
or 8 and are divisible by
numbers end in 1, 3, 5, 7,
or 9 and are not divisible by 2
Divisibility Rule 3
A number is divisible by three if the
sum of the digits is divisible by 3.
Examples:
75
369
7 + 5 = 12 12 ÷ 3 = 4 No Remainder
3 +6 + 9 = 18
Remainder
18 ÷ 3 = 6 No
Now You Try:
Which number IS NOT divisible by 3?
572
1464
Need More Practice: Numbers Divisible by 3
279
The sum is
divisible by 3.
WONDERFUL
Divisibility Rule 9
A number is divisible by 9 if the sum of
the digits is divisible by 9.
Examples:
963 9 + 6 + 3 = 18 18 ÷ 9 = 2
5445 5 + 4 + 4 + 5 =18 18 ÷ 9
=2
Now You Try:
Find the number that IS NOT divisible by
9.
9873
630
Need More Practice: Numbers Divisible by 9
5541
The sum of the digits is
divisible by 9.
Great Job!!!
Factors
One integer is a factor of another
integer if it divides that integer with a
remainder of zero.
Ex. factors of 20
1, 20
2, 10
4,5
The factors of 20 are 1, 2, 4, 5, 10, 20
Examples
1) Divisibility by 2, 5, and 10
a)
b)
1028 by 2
572 by 5
c) 275 by 10
; 1028 ends in
; 572 doesn’t
end in or
; 275 doesn’t
end in
Examples
2) Divisibility by 3 and 9
a)
b)
1028 by 3
1+0+2+8=11; 11 is
not divisible by
522 by 9
; 5+2+2=9; 9 is
divisible by
Examples
3) Using Factors
Find pairs of factors of 35
1 x 35
5x7
There can be 5 rows of
rows of students.
students or 7
Quick Check
a)
b)
c)
d)
e)
f)
g)
h)
Yes; the last digit is 0
No; the last digit is not 0
No; the last digit is not 0, 2, 4, 6, or 8
Yes; the last digit is 2
No; the sum of the digits is not divisible by
9
No; the sum of the digits is not divisible by
3
Yes; the sum of the digits is divisible by 3
Yes; the sum of the digits is divisible by 9
Quick Check (2)
a.
b.
c.
d.
1,
1,
1,
1,
2, 5, 10
3, 7, 21
2, 3, 4, 6, 8, 12, 24
31
Quick Check (3)

There could be 6 rows of 6 students, 4
rows of 9 students or 9 rows of 4
students.
Objective: Students will
be able to identify
factors and use
divisibility rules
Definition

Prime Number – a number
that has only two factors, itself
and 1.
7
7 is prime because the only
numbers
that will divide into it evenly are
1 and 7.
Examples of Prime
Numbers
2, 3, 5, 7, 11, 13, 17
Special Note:
One is not a prime number.
Definition

Composite number – a
number that has more than two
factors.
8
The factors of 8 are 1, 2, 4, 8
Examples of Composite
Numbers
4, 6, 8, 9, 10, 12, 14
Special Note:
Every whole number from 2 on i
either composite or prime.
Our Lonely 1
It is not prime
because it does
not have exactly
two different
factors.
It is not
composite
because it does
not have more
than 2 factors.
Special Note:
One is not a prime nor
a composite number.