Download Solving Linear Equations

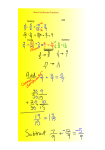
Solving Linear
Equations
Solving Linear Equations
Example 1
x 3 8
3 3
x 5
It’s obvious what the answer is.
However, we need to start with
the basics and work our way up
because we need to make sure
that we have GREAT
fundamentals in math. In other
words, we need to know WHY
we do things other than
“That’s what my teacher told
me to do.”
Next question: why do we
subtract the three?
Solving Linear Equations
Example 2
2x  5  9
When you are solving an
equation, you are undoing
the problem. Therefore
you use the order of
operations in reverse
order. Let me explain…
Most people know that the first
thing you should do on this
problem is add five to both sides.
But why? Why not divide by the
two first? Why not move the
nine? Why is the five first?
We move the five rather than the
nine because the five is on the
same side of the equals sign as
the variable. We move the five
before we move the two
because of the order of
operations.
Solving Linear Equations
ORDER OF OPERATIONS
P ARENTHESES
E XPONENTS
MULTIPLICATION
DIVISION
A DDITION
S UBTRACTION
Solving Linear Equations
ORDER OF OPERATIONS
PARENTHESES
PEMDAS is used for
EXPONENTS
evaluating expressions with
MULTIPLICATION no variables,2 like this:
4(3  5)  3(7)  2
DIVISION
ADDITION
SUBTRACTION
Solving Linear Equations
ORDER OF OPERATIONS
SUBTRACTION
However, since we are
ADDITION
solving an equation, we are
UNDOING the order of
DIVISION
operations. Therefore, we
MULTIPLICATION need to UNDO things in
reverse order.
EXPONENTS
PARENTHESES
Solving Linear Equations
Example 2
2x  5  9
5 5
2x  14
2
2
x7
We add five to both sides since it
is subtracted from the variable.
We move the two by division
because it is multiplied times the
variable.
Solving Linear Equations
Example 2
2x  5  9
5 5
2x  14
2
2
x7
One last thing before we move
on. When I say that x = 7, I am
saying TWO things. What are the
two things?
The first thing that I am saying is
that 7 works. That means when I
plug 7 in for the x, I get a TRUE
statement.
2x  5  9
2(7)  5  9
14  5  9
99
Solving Linear Equations
Example 2
2x  5  9
5 5
2x  14
2
2
x7
One last thing before we move
on. When I say that x = 7, I am
saying TWO things. What are the
two things?
What else am I saying?
I am saying that NOTHING
ELSE works.
2x  5  9
2(3)  5  9
65  9
1 9
Solving Rational Equations
Example 3
3x  8  6
8 8
3x  14
3
14
x
3
3
This one is for you to try.
Can you get a fraction for an
answer?
Solving Rational Equations
Example 4
5x  6  2 x  9
 2x
 2x
3x  6  9
6 6
3x  15
3 3
x 5
Why is this problem different
than the others we’ve seen so
far?
Because there’s a variable on
both sides of the equation.
Can you check your answers?
Solving Rational Equations
Example 4
5x  6  2 x  9
5(5)  6  2(5)  9
25  6  10  9
19  19
There are three rules when
checking your answers:
1) Always plug the answers
back into the ORIGINAL
problem,
2) Never cross the equals sign,
and
3) Use the order of operations
on each side of the equation.
Solving Rational Equations
Example 5
3( x  4)  5( x  6)  2( x  1)
3x 12  5x  30  2x  2
3x 12  7x  32
 3x
 3x
12  4x  32
 32
 32
44  4x
11  x
Before working this
problem, get rid of
the parentheses by
distributing the
outside numbers.
If there are like terms
on the same side of
the equals sign, just
combine them as
they are.
Solving Rational Equations
Example 5
3( x  4)  5( x  6)  2( x  1)
3(11  4)  5(11  6)  2(11  1)
3(15)  5(5)  2(10)
45  25  20
45  45
Can you check
these?
Solving Rational Equations
Example 6
3( x  1)  2( x  5)  5( x  1)  2( x  3)
3x  3  2x 10  5x  5  2x  6
5x  7  3x 11
 3x
 3x
2x  7  11
7 7
2x  4
x2
Don’t forget to
multiply by the
number and the sign
in front of the
number.
Solving Rational Equations
Example 7
x 3 x 1
  
3 4 4 2
3
8   6
4
3
20   12
5
4
9  
9
4
5
12  
6
1
8  
4
Fractions!!!
10
2
 2  14
7  
 11  11
You only need to know one
“trick” to solve equations
with fractions. To multiply a
fraction times a whole
number, divide the bottom
into the whole number, then
multiply what’s left.
Let’s practice a couple of
those before we work this
equation.
Solving Rational Equations
Example 7
x 3 x 1
12 (    )
3 4 4 2
4x  9  3x  6
 3x
 3x
x  9  6
9 9
x  15
Back to the problem.
Find the common denominator of
all of the fractions and multiply
everything by that.
Remember, to multiply fractions
times whole numbers, divide the
bottom into the whole number,
then multiply what’s left.
Solving Rational Equations
Example 8
x 3
x
15 (   2  )
3 5
5
5x  9  30  3x
 3x
 3x
8x  9  30
9 9
8x  21
21
x
8
Remember, to multiply fractions
times whole numbers, divide the
bottom into the whole number,
then multiply what’s left.
Solving Rational Equations
Example 10
3( x  4)  3( x  6)
3x  12  3x 18
 3x
 3x
12  18
O
What happened that
is different from the
other problems?
If the variables go away, then
the answer is either “no
solutions” or “all real
numbers”.
It’s “no solutions” if what’s
leftover is a false statement.
It’s “all real numbers” if what’s
Solving Rational Equations
Example 11
2(3 x  6)  3(2 x  4)
6x 12  6x 12
 6x
 6x
12  12
ALL REAL NUMBERS
Remember, if the
variables go away, then
the answer is either “no
solutions” or “all real
numbers”.
It’s “no solutions” if
what’s leftover is a false
statement.
It’s “all real numbers” if
what’s leftover is a true
statement.
Solving Rational Equations
Example 12
5( x  2)  2( x  5)
5x 10  2x 10
 2x
 2x
3x  10  10
 10  10
3x  0
3 3
x0
Is this “no solutions” or
“all real numbers”?
Neither. Remember,
it’s only one of those if
the VARIABLES go
away. Just keep on
working this problem.
Answers :
Solving Rational Equations
Pair Practice: Solve these problems
with a partner.
1)
2)
3)
4)
5)
1)3
2) 8
3)7
9
5x 10  25
4)
8
3x  4  5x 12
5)
4( x  3)  2( x  1)
3( x  2)  2( x  4)  x  3  4( x  1)
5(2 x  3)  2(5 x  1)
Solving Rational Equations
Answers to worksheet #1: 1) 3
2)  36
3)  17
4)  12
8
5)
5
6)  4
13
7)
4
3
8)
9)3
10)
 14
11)
3
12)
13)
32
14)
3
1
15)
4
 234
16)
25
The Rules are very simple. Be the first person to identify
the mistake made in the following problems, raise your
hand and hollar “Hey, Stupid!” The first correct answer
wins you five bonus points on the Chapter Test. Once you
win once, you cannot win again until next chapter.
It’s time for…
HEY STUPID!!!
Solving Rational Equations
HEY STUPID!!!
#1
5( x  1)  3( x  3)
5x  5  3x  3
 3x
 3x
2x  5  3
5 5
2x  8
2 2
x  4
Didn’t distribute the 3
in the first step.
Solving Rational Equations
HEY STUPID!!!
#2
2x  5  3
3 3
2x  2
2 2
x 1
Supposed to subtract
the 5 instead of the 3.
Solving Rational Equations
HEY STUPID!!!
#3
5(3x  1)  3(5 x  3)
15x  5  15x  9
 15x
 15x
5  9
ALL REAL NUMBERS
Should be no solutions,
because the statement
that is leftover is NOT
true.
Solving Rational Equations
HEY STUPID!!!
#4
4( x  1)  3( x  3)  2( x  1)
4x  4  3x  9  2x  2
4x  4  x 11
Didn’t distribute the
x
x
negative in the first
step.
3x  4  11
4 4
3x  15
3 3
x  5
Solving Rational Equations
Hey, Stupid!
#5
x 3
x
6 (   4 )
3 2
2
2 x  9  4  3x
 3x
 3x
5x  9  4
9 9
5x  5
x  1
You have to multiply
EVERYTHING by the common
denominator. They didn’t
multiply the four by six.