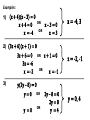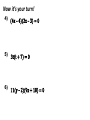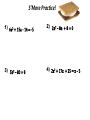Download (n + 2) = 0

Warm-Up
Factor the following completely:
Answers:
1. x  5 x  14
( x  7)( x  2)
2. 2 x  14 x  24
2( x  3)( x  4)
2
2
2
x
 10 x  24
3.
4. 3x  27 x  60
2
( x  12)( x  2)
3( x  4)( x  5)
Lesson 13.7
Solving Equations by Factoring
Objectives:
1. Learn and understand what the Zero Product Property means.
2. Use the Zero Product Property to solve quadratic equations
that have already been factored.
3. Understand that a quadratic equation must be equal to zero
before factoring it.
4. Solve an equation by factoring it.
Have you realized?
That every question we have reviewed so
far has not had an “=“ sign.
All questions so far have been FACTOR,
SIMPLIFY, or DISTRIBUTE.
Today’s lesson we will include SOLVE BY
FACTORING into the mix.
The Zero Product Property Review from
7th grade states:
If the product of two or more factors is zero, then at least one of the factors
must be zero.
Or in other words, if the problem equals zero, at least on of the “parts” has to
be a zero.
Examples:
4x = 0
x=0
zy = 0
z = 0 or y = 0
6wk = 0
w = 0 or k = 0
The following is a Quadratic Equation that is in
factored form:
(x + #)(x + #) = 0
(x + a) is one
factor
(x + b) is
another factor
Using the Zero Product Property we know that if at
least one set of parentheses (one set of bubbles)
equals a zero, then the entire problem will “zero out.”
Example: What number
can I plug into each bubble
to make it equal zero?
 x  7 x  1  0
x = 7 and x = -1
Technically you take whatever is inside the bubble and set it equal
to zero, like a mini equation and solve.
Examples:
1)
(x + 4)(x – 3) = 0
x+4=0
x = -4
OR
OR
x–3=0
x =3
x = -4, 3
2) (3z + 6)(z + 1) = 0
3z + 6 = 0
3z = -6
x = -2
3)
OR
OR
z+1=0
z = -2, -1
x = -1
y(2y – 8) = 0
y=0
OR
y =0
OR
2y – 8 = 0
2y = 8
y =4
y = 0, 4
Now it’s your turn!
4) (4x – 4)(2x – 3) = 0
5) 3t(t + 7) = 0
6) 11(y – 2)(9x + 18) = 0
Now that we know the zero product property
and how to use it, let’s apply it and solve
some quadratic equations! (Keep in mind
this is going to require us to rearrange, factor,
and solve)
This is gonna
be awesome!
To solve a Quadratic Equation by factoring,
it must first be equal to zero:
ax2 + bx + c = 0
Examples:
1) x2 + 3x + 2 = 0
2)
3k2
3k2
3) 2n2 + 3n + 1 = -3n – 3
+3
+3
– 3k – 8 = -2
2n2 + 3n + 4 = -3n
– 3k – 6 = 0
2n2 + 6n + 4 = 0
+2 +2
+ 3n
+ 3n
Once the Quadratic Equation is equal to zero the next
step to solving it is by factoring:
Example:
2n2 + 6n + 4 = 0
2 (n2 + 3n + 2) = 0
2 (n + 1)(n + 2) = 0
(n + 1)(n + 2) = 0
STEP 1: Factor out the GCF
STEP 2: Factor the Quadratic Equation
STEP 3: Divide both sides by 2
After factoring, use the Zero Product Property to finish solving
the quadratic equation:
(n + 1)(n + 2) = 0
n+1=0
OR
n = -1, -2
n+2=0
STEP 4: Solve both equations
STEP 5: Check answer by substituting
back into original equation
Let’s do a recap of the steps…(this might be something you want
to write down for future reference!)
Step 1: Make sure the entire equation is set = to 0.
(If it is not, you better do some rearranging to get all letters and
numbers on one side!)
Step 2: Pull out a Greatest Common Factor. (If you can)
(In other words, pull out a number or variable that divides all terms
evenly!)
Step 3: Factor the leftover quadratic into two binomials.
(Meaning you should have 2 sets of parentheses) ex. (x + 2)(x – 3)
Step 4: Use the Zero Product Property to set each binomial equal to 0.
Step 5: Solve each binomial for the variable.
Step 6: “GLADE” IT! (“Plug it in, plug it in”) to check your work and see
if your answers make sense.
S’More Practice!
1) 6a2 + 15a – 14 = -5
2) 2n2 – 8n + 8 = 0
3) 5b2 – 80 = 0
4) 2x2 + 17x + 25 = x – 5
And still s’more practice!
5)
2a2
– 16a + 34 = 4
7) 3b2 – 18b + 27 = 0
6) 2n2 + 8n – 5 = -5
8) 6x2 + 12x – 29 = 3x – 2
Homework:
Complete the 13.7
(And bring in smores to your math teacher!)