Download SE207 Modeling and Simulation

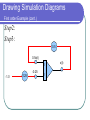
SE207 Modeling and Simulation
Lab # 3: Analog Simulation of a
First Order System (RC circuit)
Objectives

The objective of this experiment is to
simulate a first order system (an RC
circuit) and study its behavior.
Equipment
GP-6 Analog Computer
 X-Y plotter

First Order Systems

First order systems are modeled by first order
Differential equations.
dx(t )
 k x(t )  f (t )
dt
 Any circuit containing a resistor and a
capacitor can be modeled by a first order
model.
RC Circuit
The RC circuit
is modeled by
the equation.
+
_
dvc (t ) 1
1

vc (t ) 
E (t )
dt
RC
RC
vc (0)  v0
R
C
Vc (t)
Time constant of a First Order System
The final value of Vc(t) =E
 The time at which Vc(t)=0.63 * final value
is called the time constant of the system.

Vc(t)
Final value of Vc(t)
63% of Final value of Vc(t)
t
Time constant
Time constant
Time constant depends on C and R
 Larger time constant means the
capacitor needs longer time to charge.

Drawing Simulation Diagrams
Problem : Draw Simulation diagram for
d 2 x(t )
dx(t )
a
 bx(t )  f (t )
2
dt
dt
x ( 0)  x 0
dx(t )
 x1
dt
Drawing Simulation Diagrams
Step 1 : Solve for the negative of the highest order derivative
d 2 x(t )
dx(t )
a
 bx(t )  f (t )
2
dt
dt
d 2 x(t )
dx(t )

a
 bx(t )  f (t )
2
dt
dt
We need to feed these
dx(t )
a
 bx(t )  f (t )
dt
as inputs to an integrator and the
d 2 x(t )
dx(t )
output of the integrator will be 
dt 
2
0
dt
dt
t
Drawing Simulation Diagrams
Step 2 : Other derivative s and x(t) can be obtained using integrator s
Step 3 : Use potentimet ers and the right gain for the inputs
of the integrator s complet th e simulation diagram
Drawing Simulation Diagrams
First order Example
Problem : Draw Simulation diagram for
dx(t )
2
 x(t )  0.5
dt
x(0)  0
0.5x(t)
Step1 :
dx(t )
-0.25

 0.5 x(t )  0.25
dt
x(t)
Drawing Simulation Diagrams
First order Example (cont.)
Step 2 :
Step3 :
0.5
0.5x(t)
1
-0.25
-1.0
0.25
1
x(t)
Procedure
Write the system of equation in a form
suitable for drawing analog simulation
diagram
2. Draw the analog simulation diagram
corresponding to the value given in the table.
Assume E(t) = 1.0 Volt and Vc(0)=0
1.
Time R
10 Sec 1
20 Sec 1
C
10
5
Procedure (cont.)
3.
4.
5.
6.
7.
For the first set of values, connect the analog
computer circuit on the GP-6 using one integrator.
Set the Y/Pot-address to GND/X and mode selector
to OPR.
Select the output amplifier from the X-address,
press OP button and monitor the output of the
system Vc(t)
Repeat step (4) and plot the output on the X-Y
plotter
Repeat steps (1- to 5) for the second set of values of
R and C.
Report
Your report should include the following
 A plot of the output voltage for the two cases
 Estimates of the system’s time constants in
both cases
 Comparison of the theoretical and
experimental values of the time constants in
both cases
 Comments and conclusions on your
observations