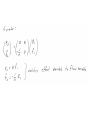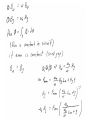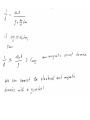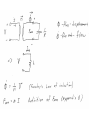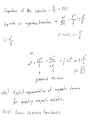Download Lumped Modeling with Circuit Elements, Ch. 5, Text

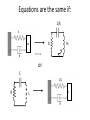
Lumped Modeling with Circuit
Elements, Ch. 5, Text
• Ideal elements represent real physical
systems.
– Resistor, spring, capacitor, mass, dashpot,
inductor…
– To model a dynamic system, we must figure out
how to put the elements from different domains
together.
– Alternatives include numerical modeling of the
whole system. Lumped element modeling offers
more physical insight and may be necessary for
timely solutions.
Example. Electrical: Resistor-InductorCapacitor (RLC) system.
C
R
i
L
No power source, transient
response depends on initial
conditions
B1, B2 depend on initial conditions
Example. Mechanical: Spring-MassDashpot system.
x
k
m
No power source, transient
response depends on initial
conditions
b
B1, B2 depend on initial conditions
Equations are the same if:
1/k
k
b
m
.
I <-> x
b
.
x
m
or
C
1/C
R
L
L
R
Goal: Simulate the entire system.
• Usual practice:
– Write all elements as electrical circuit elements.
– Represent the intradomain transducers (Ch. 6)
– Use the powerful techniques developed for circuit
analysis, linear systems (if linear), and feedback
control on the whole MEMS system.
Senturia generalizes these ideas.
• Introduce conjugate power variables, effort,
e(t), and flow, f(t).
• Then, generalized displacement, q(t)
• And generalized momentum, p(t)
e . f has units of power
e . q has units of energy
p . f has units of energy
Variable Assignment Conventions
• Senturia uses e -> V, that is, effort is linked
with voltage in the electrical equivalent
circuit. He explains the reasons (for example
potential energy is always associated with
energy storage in capacitors).
Following Senturia’s e -> V convention:
• For effort source, e is
independent of f
• For flow source, f is
independent of e
• For the generalized
resistor, e=e(f) or f=f(e)
• Linear resistor e=Rf
• Electrical, V=RI
• Mechanical, F=bV
• For the generalized capacitor (potential energy):
•For a linear electrical capacitor:
ε – permitivity
A – area
G – Gap
•The mechanical equivalent is the linear spring.
(Check
in table.)
Cspring = 1/k
•Generalized Inductor or inertance (kinetic
energy?)
Linear inertance: momentum
flow
m – mass
v – velocity
p – momentum
momentum?
Electrical?
But what is this???
???