Download Student Biographies

Electronics - Operational Amplifiers
Introduction







The basic operational amplifier or Op Amp is a very important circuit to study because it
is so widely used.
Op Amps were initially made from discrete components like vacuum tubes and resistors
with transistors eventually replacing vacuum tubes
In the mid 1960’s the first integrated circuit op amps were produced (mA 709)
 It had quite a few transistors and resistors compared to the discrete versions it
replaced
 Its characteristics were poor by today’s standards
 It was expensive, but
 It was all on a single silicon chip and it ushered in a new era in analog
electronic circuit design
 It was more reliable than discrete op amps
Engineers started using them in large quantities and the price dropped dramatically
from over ten dollars each to 30 cents each and the reliability continued to increase
The op amp is a very versatile circuit and can be used in numerous other circuits. The
integrated circuit op amp characteristics come pretty close to that of an “ideal”
amplifier. The near “ideal” behavior makes it much easier to design with op amps
By the end of this group of lecture sessions the reader should be able to design some
fairly complex circuits using op amps
We will start by treating a op amp as a “building block” and describe its terminal
characteristics and save a detailed discussion about what is inside an op amp for a later
course (EGRE 307)
© REP 5/23/2017 EGRE224
Page c2.1-1
Electronics - Operational Amplifiers
The Op Amp Terminals


The terminals of a circuit can be divided up into different groups based on their
functions, for example the power supply terminals, the signal terminals, etc.
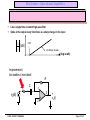
The op amp circuit has three signal terminals, two inputs (#1 , #2) and one output (#3) as
shown on the figure below
1
inputs
2

3
+
output
The amplifier requires dc power to operate. Most op amps require two dc power
supplies to operate. Most of the time the two supplies are equal in magnitude but
opposite in polarity, for example a positive voltage supply +V (relative to ground) and a
negative voltage supply -V (relative to ground) connected to terminals #4 and #5 as
shown.
+V
1
inputs
2
4
+
3
output
5
-V
© REP 5/23/2017 EGRE224
Page c2.1-2
Electronics - Operational Amplifiers
Op Amp Terminals, continued

An op amp can use a single power supply (+10V and ground for example) but the signal
“reference” of the circuit for symmetrical behavior will then be at one half the upper
supply voltage or +5V in this case.
+5V
+10V
1
inputs
2
4
+
5
0V



3
Output signal ground
at +5V relative to
real ground
or
1
4
3
inputs +
2
5
Output Signal
ground is at
same level
as real ground
-5V
+10V
The reference grounding point in op-amp circuits is just the common terminal of the two
power supplies.
That is, no terminal of the op amp package is physically connected to ground
In many cases the power supply connections will not be explicitly shown on the
schematic. They will be omitted to reduce the “clutter” but the connections are still
implied when you draw the triangular op amp symbol.
An op amp may have other terminals for frequency compensation and for removing (or
nulling) out offset voltages.
© REP 5/23/2017 EGRE224
Page c2.1-3
Electronics - Operational Amplifiers
Exercise

What is the minimum number of terminals required for a single op amp?
 Five - Two Inputs, Two power connections (either +/-, symmetric or + and Ground,
non-symmetric) and one signal output referenced to ground (symmetric) or 1/2 the
positive supply in a non-symmetric configuration

What is the minimum number of terminals required for an integrated circuit package
which contains four op amps (assume all four share power supplies)?
 Fourteen, four pairs of inputs, two power connections and four outputs
© REP 5/23/2017 EGRE224
Page c2.1-4
Electronics - Operational Amplifiers
The Ideal Op Amp





The op amp is designed to sense the difference between the voltage signals applied to its two
inputs (v2-v1), and multiply this by a number A, and cause the resulting voltage A (v2-v1) to
appear at the output terminal relative to ground. Note that v1 and v2 are also implied to be
relative to ground as shown in the figure below.
The ideal op amp is not supposed to draw any current from the signal source (it will draw
current from the power supply terminal which are not shown).
The input impedance is supposed to be infinite
The output is supposed to act as an ideal voltage source independent of the current drawn by
any load placed on the op amp.
The output impedance is supposed to be zero
The output has the same sign (is in phase with)
the input v2 and is out of phase (opposite sign)
as v1 . For this reason input terminal # 1 is
called the inverting input (distinguished by a “-”
sign) and input terminal # 2 is called the noninverting input (distinguished by a “+” sign).
The op amp only responds to the difference
signal v2-v1 and ignores any signal common to
both inputs.
1
v1
I1=0
A(v2-v1)
2
v2
I2=0
Common terminal
of the power supplies
© REP 5/23/2017 EGRE224
Page c2.1-5
3
Electronics - Operational Amplifiers
Common Signal vs. Differential Signal




The part of the signal that is the
same for both inputs is called
the common mode component
and is not amplified
If both inputs see the same
signal the DIFFERENCE (v2-v1)
is zero and there is nothing to
amplify and the output is zero.
This means that the amplifier
has rejected (not amplified)
what the two signals had in
common
An ideal opamp has infinite
common-mode rejection
For the time being we will
consider the opamp to be a
differential input single - ended
- output (output from terminal 3
to ground)
A(v2 - v1)
v2
0
v1
Vp-p
1
2 Vp-p
on each side
out of phase
Vp-p
1
2 Vp-p
on each side
in phase
© REP 5/23/2017 EGRE224
0
Page c2.1-6
Electronics - Operational Amplifiers
The Ideal Op Amp continued





The gain, A is called the differential gain (based on the difference between terminals 2 and 1)
The gain, A is also sometimes called the “open loop” gain as opposed to later on when we add
a feedback path from output to input and look at the “closed loop” gain
Opamps are direct-coupled (DC) or direct current (DC) amplifiers.
 DC amplifiers have many applications but can also pose some practical problems
IDEAL opamps amplify from zero frequency to infinite frequency, they are said to have infinite
bandwidth
The gain of an ideal opamp should approach
infinity, but then how could we make use of an
ideal opamp since any difference times infinity
would be infinity?
 We usually don’t use opamps in an open
loop configuration
 Feedback lowers the gain to practical
levels
 The value for A of a “real” opamp might be
on the order of a million
© REP 5/23/2017 EGRE224
1
v1
I1=0
A(v2-v1)
2
v2
I2=0
Common terminal
of the power supplies
Page c2.1-7
3
Electronics - Operational Amplifiers
Exercise 2.2

Consider an op amp that is ideal except that its open-loop gain A=103. The op amp is
used in a feedback circuit and the voltages appearing at two of its three signal terminals
are measured. In each of the following cases, use the measured values to find the
expected value of the voltage at the third terminal.
A) v2 = 0V, v3 = 2V
v1=-{(v3/A)-v2} = -{(2/1000)-0} = -0.002V
B) v2 = 5V, v3 = -10V
v1=-{(v3/A)-v2} = -{(-10/1000)-5} = 5.01V
C) v1 = 1.002V, v2 = 0.998V
v3=A(v2 - v1) = 1000(0.998-1.002) = 4.0V
D) v1 = -3.6V, v3 = -3.6V
v2={(v3/A)+v1} = {(-3.6/1000)+3.6} = 3.6036V
© REP 5/23/2017 EGRE224
Page c2.1-8
Electronics - Operational Amplifiers
Exercise 2.3


The internal circuit of a particular op amp can
be modeled by the circuit shown to the right.
Express v3 as a function of v1 and v2.
v3  m vd
vd  iR R v3  mRi R
1
iR  Gm v2  Gm v1  Gm v2  v1 
v1
 v3  m RGm v2  v1 

For the case when Gm = 10 mA/V, R =10kW and
m = 100, find the value of the open-loop gain A.
v3
A
 m Gm R  1000.0110,000
v2  v1 
Gmv1
3
R vd
2
v2
mvd
Gmv2
V
A  10,000
V
© REP 5/23/2017 EGRE224
Page c2.1-9
Electronics - Operational Amplifiers
The Analysis of Circuits Containing Ideal Op Amps




The Inverting Configuration
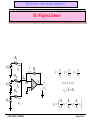
Resistor R2 is connected from the output terminal, 3, back to the inverting or negative
terminal input terminal, 1. We say that R2 applies negative feedback, if R2 were
connected between the output, 3, and the other input, 2, we would say that it was
positive feedback.
We have grounded input number 2 and applied the input signal between terminal one
and ground. This is known as a single sided input since terminal 2 does not contribute
any information to the signal (since it is grounded).
The output is taken at terminal 3 relative to ground and is called a single sided output.
Note that the impedance at terminal 3 (output) of an ideal opamp is infinite, thus the
voltage vo will not depend on the value of the current that might be supplied to a load
placed across vo.
R2
input
R1
1
vI
2
4
+
3
+
vo output
-
© REP 5/23/2017 EGRE224
Page c2.1-10
Electronics - Operational Amplifiers
Closed-Loop Gain (G) Analysis

G is defined as

We can draw the equivalent circuit for the opamp. Assume the opamp is powered up
and working and the output is finite. With a finite output and infinite gain the difference
between the inputs is negligibly small. Since terminal 2 is held at ground then terminal
one also has to be at ground (forced there by the circuit NOT connected to ground).
Using our definition we write

G
vO
vI
Av2  v1   vO
v2  v1 
or
We say that the two input terminals
are tracking each other in potential
vO
0
A
i2
R2
R2
R1
i1
1
vI
2
+
3
+
vo
vI
R1
1 0
3
v2-v1
2 +
+
_
A(v2-v1)
-
-
© REP 5/23/2017 EGRE224
+
vo
Page c2.1-11
Electronics - Operational Amplifiers
Virtual Ground


The circuit forces the two input terminals to be at virtually the same potential, they are
“virtually” shorted together. A physical connection for charge movement does not exist
but since they track each other in potential is like there is a connection (a virtual short
circuit)
If terminal 2 is grounded then we can refer to terminal 1 as a “virtual” ground. It is
forced to be at zero volts even though it is not directly connected to ground it acts like it
is.
© REP 5/23/2017 EGRE224
Page c2.1-12
Electronics - Operational Amplifiers
Back to the analysis

Since we now know v1 we can use Ohm’s law and find the current flowing through the
resistor R1.
i1 

vI  v1 vI

R1
R1
Since this current can not flow into the input terminal of an ideal op amp (infinite input
resistance) it must flow through the resistor R2 to the low impedance terminal, 3
(output). We can now apply Ohm’s law to R2 and determine vo.
vO  v1  i1R2
vO  


vI
R2
R1
but
v1  0 so
or G 
vO
R
 2
vI
R1
The negative sign for the closed loop gain indicates that the amplifier provides signal
inversion
If we apply a 50mV peak-to-peak sine-wave input signal the output will be an amplified
sine-wave with a 180 degree phase shift (inversion).
© REP 5/23/2017 EGRE224
Page c2.1-13
Electronics - Operational Amplifiers
The Effect of Finite Open-Loop Gain






How do our results change if we let the open loop gain, A, be finite?
If we let the output be denoted by vO, then the voltage difference between the inputs is
vO/A.
Since the positive input is grounded the negative input must be at - vO/A.
We can now find the current through resistor R1
v
vI    O  v  vO
A
v v
I

A
i1  I 1 

R1
R1
R1
The infinite input resistance of the op amp forces all of the current to flow through R2.
We can write another expression which contains vO.
v


vO  vI  O A 
vO  v1  i1R2    
 R2
A 
R1




Collecting terms and solving for the closed-loop gain G, we get
G
vO

vI

R2
1 

1 
R1
R2
© REP 5/23/2017 EGRE224

R1 
Note: As A approaches infinity, G approaches
the ideal value that we previously derived
A
Page c2.1-14
Electronics - Operational Amplifiers
Input and Output Resistance



As A approaches infinity the voltage at the inverting terminal approaches zero (our
virtual ground)
In order to minimize the effect of A on G we should make
R
1
2
R1
 A
If we assume an ideal op amp with an infinite input resistance the overall input
resistance of the closed loop circuit (containing the ideal op amp) will be
Ri 
vI
v
 I  R1
iI v I
R1


The value of the open loop gain, A, has very little effect on the input resistance
For a high input resistance we need R1 high, but if we want the gain to also be high we
might require R2 to be very large (maybe impracticably large). Can you think of a way to
increase the input resistance?
 The output of the inverting configuration is taken at the terminal of an ideal voltage
source (whose value is (v2-v1)A) which can supply infinite current, Rout=V/I is zero.
Ro=0
 Putting the previous results together we
have the following model of the inverting
+
+  R2 v
closed loop amplifier circuit (using an ideal
I
vI
Ri=R1
_
R1
opamp)
_
© REP 5/23/2017 EGRE224
Page c2.1-15
Electronics - Operational Amplifiers
Example 2.1

Consider the inverting amplifier configuration shown below with R1=1kW and R2=100kW.
A) Find the closed-loop gain for the cases A=103, 104, 105. In each case determine the
percentage error in the magnitude of G relative to the ideal value of R2/R1 (obtained with
A that is infinite). Also determine the voltage v1 that appears at the inverting input
terminal when vI = 0.1 V.
We can use the equation for the closed loop gain, Greal in terms of the open loop gain, A
and compare the results to the ideal closed loop gain Gideal.
 (error) 
A
Greal  Gideal
Gideal

Greal


R2


 R2
R1


R1
R2  

1   1  R  / A 
1


 100  
 100
R2
R1
v1
3
90.83
 9.17%  9.08mV
104
99.00
 1.00%  0.99mV
105
99.90
 0.10%  0.10mV
10
© REP 5/23/2017 EGRE224
 vO GvI 
v1 

A
A
where vI  0.1V
Page c2.1-16
Electronics - Operational Amplifiers
Example 2.1 continued

B) If the open-loop gain A is cut in half, from 100,000 to 50,000, what is the
corresponding percentage change in the magnitude of the closed-loop gain G?
G
vO

vI

R2
1 

1 
R1
R2

R1 

 100
 99.8

1  100
1
50,000
A

For A=100,000 G was 99.9, so cutting the open loop gain in half from 100,000 to 50,000
only changed the closed loop gain by -0.1 percent

Using negative feedback in a low gain configuration makes the circuit much more
impervious to possible variations in the open-loop gain of the op amp.
© REP 5/23/2017 EGRE224
Page c2.1-17
Electronics - Operational Amplifiers
Example 2.2


We are going to analyze a different inverting op amp circuit (see below)
Part A) Derive an expression for the closed-loop gain vO/vI
vI 

 vO  vO

0
A

i1 
i2  i1 
vI
R1
We can now write an expression for the voltage at node “X”
v x  v1  i2 R2  0 
i2
 vI
R
R2   2 vI
R1
R1
R2
X
R3
R1
vI
v I  v1 v I  0 vI


R1
R1
R1
i1
i3 
i4
0  vx
R
 2 vI
R3
R1R3
i4  i2  i3 
vO  vx  i4 R4  
R4
vI
R
 2 vI
R1 R1R3
v

R2
R
vI   I  2 vI  R4
R1
 R1 R1R3 
R R 
vO
R 
R 
R R 
   2  4 1  2    2 1  4  4 
vI
R3 
R1 
R2 R3 
 R1 R1 
i3
0
vI
+
+
vo
Ideal
© REP 5/23/2017 EGRE224
Page c2.1-18
Electronics - Operational Amplifiers
Exercise 2.4 (design)

Using the circuit shown below design and inverting amplifier having a gain of -10 and an
input resistance of 100kW. Give the values of R1 and R2.
R2
input
R1
1
vI
2
4
+
3
+
vo output
-
Ri  R1  100kW since the inverting input (terminal 1) is at virtual ground
G  10 
vO
R
R2
 2 
vI
R1
100kW
R2  1MW
© REP 5/23/2017 EGRE224
Page c2.1-19
Electronics - Operational Amplifiers
Exercise 2.5 Transresistance Amplifier

The circuit shown below can be used to implement a transresistance amplifier. Find the
value of the input resistance Ri, the transresistance Rm, and the output resistance Ro.
10kW
1
input
2
4
+
3
+
vo output
-
Ri  R1  0W since the inverting input (terminal 1) is at virtual ground
Rm 
vO
vO

 10kW
 iI  vO / 10kW
RO  0W
from the definition of the Ideal Op Amp
so the 10kW resistor is ignored since the Op Amp
output resistance is so low
© REP 5/23/2017 EGRE224
Page c2.1-20
Electronics - Operational Amplifiers
Exercise 2.5 Transresistance Amplifier continued

Part b) If a signal source of 0.5 mA in parallel with a 10kW resistor (see below) is
connected to the input of this amplifier find its output voltage.
RF 10kW
1
0.5mA
RS
10kW
2
4
+
3
+
vo output
-
Since terminal 2 is grounded terminal 1 is forced to a virtual ground
this means that both sides of the source resistance Rs are at ground and
no current flows through it. The entire 0.5 mA must flow through RF the
feedback resistor since the input impedance of the op amp is infinitely
large. Therefore
vO  iRF  0.5mA10,000  5V
© REP 5/23/2017 EGRE224
Page c2.1-21
Electronics - Operational Amplifiers
The Inverting Configuration with General Impedances


The Inverting Configuration
Replace resistors R1 and R2 with impedances Z1 and Z2 as shown below.
G s  
vO s 
Z s 
 2
v I s 
Z1 s 
where j  s
The physical magnitude and phase of the input signal of frequency 
Z2
input
Z1
1
vI(s)
2
4
+
3
output
+
vo(s)
-
© REP 5/23/2017 EGRE224
Page c2.1-22
Electronics - Operational Amplifiers
Example 2.3

Derive an expression for the transfer function of the circuit shown below. Express the
transfer function in a standard form for Bode Plots (see page 32 of Sedra and Smith 4th
edition).

Let Z1  R1 , and Z 2  R2  1

 sC2 
C2
R2
R1
1
vI
2
+
3
+
vo
-
In Bode Plot
Form
R
  2 
R1 
vO s 
 
vI s  1  sC2 R2
R2
1
sC2


R2  1
R2   1


sC
sC
vO s 
2
2



v I s 
R1
R1
vO s 
1

R1
v I s 
 sC2 R1
R2
The dc gain is K  
R2
R1
The corner frequency is
© REP 5/23/2017 EGRE224
0 
1
C2 R2
Page c2.1-23
Electronics - Operational Amplifiers
Example 2.3 continued




We could arrive at the same results regarding the circuit with impedances by using our
knowledge of the frequency dependent behavior of the capacitor.
The capacitor behaves as an open circuit at low frequencies. With the capacitor
essentially removed the circuit is the same as the resistive configuration we have
already analyzed and the gain is just -(R2/R1).
At high frequencies the capacitor acts like a short-circuit and resistor R2 will become
shorted out reducing the gain to zero at some point (frequency).
Design the circuit so that the dc gain is 40 dB with a corner (-3dB) frequency of 1kHz
and an input resistance of 1kW.
Gain in dB  20 log A  40
A  10
40
20
 100V
Adc  100V
V
V

R2
R1
 R2  100R1

The input resistance is simply R1 = 1kW since the inverting input is at ground

We can now find the capacitance value which causes the corner frequency (f0) to be at
1kHz.
1
1
R2  100R1  1001kW  100kW
0  2  f 
C2 R2

C2 
2 1,000100,000
C2  1.59nF
© REP 5/23/2017 EGRE224
Page c2.1-24
Electronics - Operational Amplifiers
Example 2.3 continued


Recall that the gain of a low pass single time constant circuit will fall off at -20dB per
decade, so that if the gain is 40 db at f0=1kHz then the gain will be zero dB two decades
higher at f=100kHz.
We also know that there is a -90 degree phase shift for frequencies more than ten times
the corner frequency, but we have to recall that in the case of the inverting configuration
there is already a -180 degree (inversion) shift so that the total phase shift is -270
degrees.
© REP 5/23/2017 EGRE224
Page c2.1-25
Electronics - Operational Amplifiers
The Inverting Integrator



Consider the inverting configuration with an impedance due to the capacitor used to
provide the feedback
We apply a time-varying input signal vI(t). The virtual ground at terminal 1 causes the
input signal to appear across the resistor and a current iI(t) to flow. This current flow
through the capacitor C since the input impedance of the ideal op amp is infinitely high.
A charge will begin to accumulate on capacitor C. If we assume that the circuit began
operating at time t=0 then at some arbitrary time t, the charge on the capacitor will be
given by
t
Q   iI t dt
t 0

t
The capacitor voltage will be
1
vC t   VC   iI t dt
C t 0

C
R
2
+
The output voltage is
t
3
+
vo(t)
-
© REP 5/23/2017 EGRE224
VC is C at t  0
1
vO t   
vI t dt  VC

RC t 0
1
vI(t)
where

The output is proportional to the
time integral of the input. The
product RC is the integrator time
constant
Page c2.1-26
Electronics - Operational Amplifiers
Another way to analyze the inverting integrator
Z1 s   R and Z 2 s  
1
sC

Looking at the frequency domain

And

The integrator transfer function has a magnitude of


The phase angle (f) is +90 degrees
Constructing a Bode plot of the transfer function shows that as w doubles the
magnitude of the response is cut in half. You can prove to yourself that this is a -6 dB
decrease for each octave (eight-fold) increase in frequency and a -20 dB decrease for
each decade increase in frequency.
The frequency at which the integrator gain becomes zero dB is known as the integrator
frequency and is simply the reverse of the integrator time constant.

Vo s 
1

Vi s 
sCR
vO
vI
© REP 5/23/2017 EGRE224
Vo  j 
1


Vi  j 
jCR
dB
Vo
1

Vi CR
-20 dB per decade
1/CR
 (log scale)
Page c2.1-27
Electronics - Operational Amplifiers
Some additional comments about the integrator





As seen on the integrator behaves like a low-pass filter with a corner frequency of zero
At zero frequency (dc) the gain is infinite (open loop gain of an ideal opamp)
The feedback element is a capacitor and at dc it would be an open circuit (no feedback
or an open loop)
Any tiny dc level in the input will theoretically produce a very large output. What really
happens is that the op amp’s output usually saturates at a level very close to the
positive or negative power supply levels of the op amp depending on the polarity of the
tiny dc level.
We can reduce the gain of the dc signal by placing a high valued resistor in parallel with
the capacitor. The high value should have little effect (no longer ideal though) on the
integrator but it will provide a dc feedback path.
© REP 5/23/2017 EGRE224
Page c2.1-28
Electronics - Operational Amplifiers
Example 2.4


Find the output produced by a Miller integrator in response to an input pulse of 1-V
height and 1-ms width. Let R=10kW and C=10nf.
From our earlier work we know the response will be of the form
t
1
vO t   
1 dt  0
RC t 0

Assume that the initial voltage
on the capacitor is zero
Substituting in the given values we find
vO t   10t
vI t 
0  t  1 ms
for
for
0  t  1 ms
1V
t
0
1ms
t
vO t 
-10V
© REP 5/23/2017 EGRE224
Page c2.1-29
Electronics - Operational Amplifiers
Example 2.4 continued


The 1V signal through a 10kW resistor produces a constant 0.1mA current through the
capacitor which causes the voltage to increase linearly
If the integrator capacitor is shunted by a 1-MW resistor, how will the response be
modified?
 The current will now be supplied into a single time constant network of Rf in
parallel with C.
 Appendix F gives a review of single time constant circuits and the resulting output
responses. The solution to the differential equation that arises is
vO t   vO   vO   vO 0  e
 Where
vO 
t
Rf C
is the final value of the output
vO     IR f  0.1mA1,000,000  100V
 and v 0   is the initial value which is zero
O
 Therfore
vO t   1001  e 10  0  t  1 ms


1
vO 1 ms   1001  e 10   -9.5V


© REP 5/23/2017 EGRE224
t
0
1ms
t
vO t 
-9.5V
Page c2.1-30
Electronics - Operational Amplifiers
The Differentiator (noise magnifier, rarely used)
i t   C
dv I t 
dt
vO t   CR
Z1 s  
dvI t 
dt
1
sC
and
Vo s 
Z
R
 2 
  sCR
1
Vi s 
Z1
sC
Vo s 
  sCR
Vi s 
1
vI(t)
2
+
3
+
vo(t)
-
© REP 5/23/2017 EGRE224

Vo  j 
  jCR
Vi  j 
Vo
 CR
Vi
R
C
Z 2 s   R

f  90
CR is the differentiator time constant
Page c2.1-31
Electronics - Operational Amplifiers


Like a single time constant high-pass filter
Spike at the output every time there is a sharp change in the input
vO
vI
dB
1/CR
+20 dB per decade
 (log scale)
Improvement,
but makes it non-ideal
R
C
1
vI(t)
2
+
3
+
vo(t)
-
© REP 5/23/2017 EGRE224
Page c2.1-32
Electronics - Operational Amplifiers
The Weighted Summer
R1
v1
i
i1
R2
v2
i
i2
R3
v3
Rf
i1 
1
0V
2
+
3
+
vo
-
i3
© REP 5/23/2017 EGRE224
v1
R1
i2 
v2
R2
i3 
v3
R3
i  i1  i2  i3
vO  0  iR f
R
R
R

vO   f v1  f v2  f v3 
R2
R3 
 R1
Page c2.1-33
Electronics - Operational Amplifiers
Exercise 2.6


Consider a symmetrical square wave of 20-V peak-to-peak, zero average, and two millisecond period applied to a Miller integrator. Find the value of the time constant RC such
that the triangular waveform at the output has a 20 Volt peak-to-peak amplitude.
Refer back to example 2.4
© REP 5/23/2017 EGRE224
Page c2.1-34
Electronics - Operational Amplifiers
The Non-Inverting Configuration


The Non-Inverting Configuration
The input signal vi is applied directly to the positive input terminal while one terminal of
R1 is grounded
R2
R1
1
Virtual short
input
2
vI(s)

4
+
3
output
+
vo(s)
-
Analysis,
 Assuming that the op amp is ideal with infinite gain, a virtual short circuit exists
between the two input terminals and the difference input signal is
v2  v1 
vo
and since v2  v1
A
vo  0 since A  
 since the voltage at the inverting terminal (is equal to that at the non-inverting
terminal) is equal to vI we can determine the current through resistor R1.
© REP 5/23/2017 EGRE224
Page c2.1-35