Download VU1 Electricity 2009

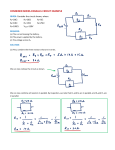
VCE Physics
Unit 1
ELECTRICITY
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Unit Outline
Apply the concepts of Charge (Q), Electric Current (I), Potential Difference (V), Energy (E)
and Power (P), in electric circuits.
Analyse electrical circuits using the relationships I = Q/t, V = E/Q, P = EIt = VI, E = VIt.
Model Resistance in Series and Parallel using:,
Potential Difference versus Current (V-I) Graphs
Resistance as the Potential Difference to Current ratio, including V/I = R =
constant for ohmic devices.
Equivalent effective resistance in arrangements in:
series: RT = R1 + R2 + R3 + …..
parallel: 1/RT = 1/R1 + 1/R2 + …..
Model simple electrical circuits such as car and household AC electrical systems as
simple direct current (DC) circuits.
Model household electricity connections as a simple circuit comprising fuses, switches,
circuit breakers, loads and earth.
Identify causes, effects and treatment of electric shock in homes and relate these to
approximate danger thresholds for current and time.
Investigate practically the operation of simple circuits containing resistors, including
variable resistors, diodes and other nonohmic devices.
Convert energy values to kilowatt-hour (kWh)
Identify and apply safe and responsible when conducting investigations involving
electrical equipment and power supplies.
Chapter 1
The Basics
1.0 Electric Charge
Atoms consist of a nucleus,
containing protons and neutrons,
with electrons circulating around it.
Electric Charge is a property of
some atomic particles.
Which ones ?
Protons and Electrons.
These two particles carry an
The UNIT of
equal and opposite electric
Electric Charge
charge.
Protons carry a charge of
is the
This charge is the smallest
+1.6 x 10-19 Coulombs
COULOMB,
known amount of charge that
Electrons carry a charge of
Symbol (C).
exists independently.
– 1.6 x 10-19 Coulombs
This charge is called the
If each electron (or proton) carries such a small
“ELEMENTARY CHARGE”
charge, a large number would be needed to
The charge carried by the
make up 1 Coulomb of charge.
Proton is DEFINED to be
POSITIVE.
The charge carried by the
Electron is DEFINED to be
NEGATIVE.
Charge
1. How many electrons in 1 coulomb of charge ?
1 electron carries 1.6 x 10-19 C
So 1 Coulomb of charge will have 1/(1.6 x 10-19) electrons
= 6.25 x 1018 electrons
2. How many electrons in 7.5 C of charge ?
1C has 6.25 x 1018 electrons so 7.5 C will have 7.5 x 6.25 x 1018
= 4.69 x 1019 electrons
1.2 Electric Current
When electric charges are
made to move or flow an
ELECTRIC CURRENT
(Symbol I) is said to exist.
The SIZE of the Current
depends on the number of
Coulombs of Charge
passing a given point in a
given Time.
The Unit of Current is the
Ampere often shortened to
Amp (Symbol A)
Mathematically:
I = Q/t
Where:
I = Current in Amps
Q = Charge in Coulombs
t = Time is Seconds
Electric current has the property of
starting immediately a circuit is complete
and stopping immediately a circuit is
broken.
Once the current is flowing it stays the
same all around the circuit.
1 Coulomb passing this point
in 1 second = 1 amp of current
Current flowing along wire
So, in 1 second 6.25 x 1018 electrons pass this point
Current
3. Calculate the current flowing if 3.57 Coulomb of charge passes a point in
1.25 sec.
I = Q/t = 3.57/1.25 = 2.86 Amp
4. If 5.62 A of current flows through a wire in 0.68 sec.
(a) How much charge has been moved ?
I = Q/t  Q = It = (5.62)(0.68) = 3.82 C
(b) How many electrons were needed to transport the charge in (a) ?
If 1 C of charge is carried by a total of 6.25 x 1018 electrons, then 3.82 C is
carried by (3.82)( 6.25 x 1018) = 2.39 x 1019 electrons
5. If a current of 125 A resulted from the movement of 225 C of charge, for
how long did the current flow ?
I = Q/t  t = Q/I = 225/125 = 1.8 sec
1.3 Conventional versus Electron
Current
In Direct Current (DC) electric
circuits, the current always flows
in one direction.
On circuit diagrams, it is ALWAYS
shown as flowing from the
positive to negative terminal of the
power source.
BUT, we know that a current is a
stream of electrons (negative
particles), which must travel in the
other direction.
What’s going on ?
It is a quirk of history that the current
direction is shown this way.
Electric currents were discovered
before the electron.
It was thought that the charge
carriers were positive and the current
must flow this way,
Never shown on
circuit diagrams
This means the current carriers
must be positively charged because
they will be repelled (like charges
repel) from the positive terminal,
and attracted (unlike charges
attract) to the negative terminal.
Protons are the Positive particles.
Wire connected
to a Battery
Electron
Conventional
Current
Current
Always shown on
circuit diagrams
Conventional vs Electron Current
6. Currents shown on circuit diagrams;
A: are from the negative to the positive terminal of the power supply and are called
electron currents
B: are from the positive to the negative terminal of the power supply and are called
conventional currents
C: are from the positive to the negative terminal of the power supply and are called
electron currents
D: are from the negative to the positive terminal of the power supply and are called
conventional currents
1.4 Potential Difference
For a current to flow around a circuit a “driving force”
is needed.
This driving force is the difference in VOLTAGE
between the start and the end of the circuit.
The larger the current you want the greater the
Small Drop =
Potential Difference (Voltage Difference) you require.
Low Pressure
Potential Difference (P.D.) is best understood
Low output
using the water analogy:
= low
A short drop between storage and tap gives
current
low water pressure = a low P.D.
Large Drop =
High
Low output from the tap = low current.
Pressure
SO A SMALL P.D. CAN ONLY DRIVE A SMALL
CURRENT.
A large drop between storage and tap gives
high pressure = Large P.D.
High output at the tap = high current
High output
SO A LARGE P.D. CAN DRIVE A LARGE
= High
CURRENT.
current
Strictly, Potential Difference is DEFINED as a
measure of the energy given to the charge carriers
(the electrons) for them to complete their job, that
is, to travel once around the circuit.
1.5 Potential
Difference
(2)
Where:
Mathematically:
V = E/Q
V = P.D. measured in Volts (V)
E = Electrical Potential Energy in Joules (J)
Q = Electrical Charge in Coulombs (C)
This means that by passing through a
P.D. of 1 Volt, 1 Coulomb of charge
picks up 1 J of energy, or more simply
1 V = 1 JC-1
In this case, each coulomb passing through the
battery will pick up 12 J of energy.
(The energy is used up in lighting the globe)
Answer: 24 J
The Battery P.D. is now increased to 24 V.
How many Joules of energy will each coulomb now
pick up ?
There are many terms used in texts to describe Voltage, some of these include
Potential, Potential Difference, Potential Drop, Voltage Drop, Voltage Difference
At this stage of your studies you can take them all to mean the same thing. The
preferred term for the VCAA examiners in Potential Difference
One further voltage, EMF (Electro Motive Force), while still measured in volts, is
slightly different and cannot be grouped with the other terms.
Voltage
7. One coulomb of charge passing through a battery picks up 15 J of
energy. What Potential Difference did the charge pass through ?
V = E/Q = 15/1 = 15 V
8. An external circuit is connected to a 24 V battery. If 6.5 C of charge passes
through the battery.
(a) How much energy does each coulomb of charge pick up in passing
through the battery ?
Each Coulomb will pick up 24 J of energy in passing through the battery
(b) How much energy (in total) has the battery supplied to the charge passing
through it
V = E/Q  E = VQ = (24)(6.5) = 156 J
1.6 Electrical Energy
The Charge Carriers in a circuit obtain their
Mathematically
energy from a power source or power supply.
E = VQ
The amount of energy (E) the charge carriers
and since Q = It
pick up depends upon the size of the voltage
Substituting we get E = VIt
difference through which they are forced to
Where:
travel.
E = Electrical Energy (J)
Since energy transferred = work done, another
V = Voltage (V)
way of defining electrical energy (E) is by the
Q = Charge (C)
work done on the charge (Q) in passing
I = Current (A)
through a Voltage (V)
t = Time (s)
An external wire connected to a battery will have
electrons flowing through it as shown.
In completing the circuit inside the battery, the
electrons need to flow from the positive to the
Electron
negative terminal.
Current
They will not do this willingly and must be forced through
the battery.
The work done on the electrons increases their electrical
energy and gives them enough energy to do another trip
around the external circuit.
Electrical Energy
9. A current of 4.2 A is being driven around a circuit by a Potential Difference of 87
V. If the circuit is allowed to operate for 36 s, how much energy has been
transferred to the charge carriers ?
E = VIt = (87)(4.2)(36) = 1.32 x 104 J
10. A total of 1.2 x 103 J of electrical energy has been transferred to the charge
carriers in a circuit driven by a 48V battery. If the circuit is switched on for 12
minutes, how many mA (milliamp) of current will have flowed during this time ?
E = VIt  I = E/Vt = (1.2 x 103)/[(48)(12 x 60)] = 0.035 A = 35 mA
11. A circuit is switched on for 6.5 minutes in that time 3.5 x 104 J of energy
has been transferred to the charge carriers. If the current flowing was 11.3
amps, calculate the Potential Difference of the power supply driving that
current.
E = VIt  V = E/It = (3.5 x 104)/[(11.3)(6.5 x 60)] = 7.9 V
1.7 Electrical Energy (2)
The energy picked up by the charge carriers is
used up in “driving” whatever device is
connected to the external circuit.
Here we have an incandescent light globe as
part of a circuit.
U joules of electrical energy transferred to Heat and Light
Q coulombs of electricity carrying
U joules of energy enter here
Q coulombs of electricity leave here
Current flowing along wire
Charges have High Energy here
Voltage Drop
= V volts
Charges have low energy here
1.8 Electric Power
Electric Power is DEFINED as the
Time Rate Of Energy Transfer or
the Time Rate Of Doing Work.
Mathematically:
P = E/t
And since
E = VIt
Substituting we get P = VI
Where
P = Power (in Watts, W)
E = Electrical Energy (J)
V = Voltage (V)
I = Current (A)
t = Time (s)
Using Ohm’s Law (See Chapter 2.) The
Power formula can be rewritten as:
P = VI = I2R = V2/R
Electrical Power
12. Calculate the power consumed by an electric drill operating at 240 V and 7.5 A.
P = VI = (240)(7.5) = 1800 W
13. An electric oven consumes 1.5 x 107 J of energy while cooking a roast. If the
roast took 2 hours to cook, at what power is the oven operating (quote your answer
in kW) ?
P = E/t = (1.5 x 107)/ (2 x 60 x 60) = 2.1 x 103 W = 2.1 kW
14. An electric kettle is rated at 3000 W. It is fitted with a 15 Amp safety switch. If
it is connected to a 240 V supply will the safety “trip” (switch off) ? Back up your
answer with a calculation.
No; P = VI  I = P/V = 3000/240 = 12.5 A less than the 15 A safety switch rating
15. The kettle mentioned in Q 14 is taken on a world trip by its owner. In America
(where the mains supply operates at 110V) he plugs it into a wall socket. Will the
safety switch trip now ? Back up your answer with a calculation.
Yes; P = VI  I = P/V = 3000/110 = 27.3 A greater than safety switch rating
1.9 Common Electrical Symbols
Single Cell
Battery
A.C. Power Supply
Earth or Ground
Switch
Crossed Wires - Joined
Crossed Wire
not Joined
Fixed Resistor
Variable Resistor
Diode
Capacitor
V
A
G
Voltmeter
Ammeter
Galvanometer
Globe
LED
Electrical Components
16. Identify the numbered components in the circuits below
1
(a)
(b)
A
V
3
2
4
2
1
3
5
6
4
5
G
(a) 1 = Variable Resistor, 2 = AC Supply, 3 = Ammeter, 4 = Lamp, 5 = Earth, 6 = Switch
(b) 1 = Voltmeter, 2 = Battery, 3 = Capacitor, 4 = Galvanometer, 5 = Fixed Resistor
1.10 Series and Parallel
Electrical components can only be
connected together in one of two
ways:
Series – where components are
connected end to end
Series
Parallel
Parallel - where components are
connected side by side.
1.11 A Typical Electric Circuit
An electric circuit contains a number
of components, typically:
•A Power Supply
•Connecting Wires
•Resistive Elements
•Meters
This power supply is a
D.C. Supply (a Battery),
and it drives the current
in one direction only.
Connecting wires are
drawn as straight lines
with right angle
bends.
They are always
regarded as pure
conductors having no
resistance.
Circuit diagrams are usually drawn in
an organized manner with connecting
wires drawn as straight lines and the
whole diagram generally square or
rectangular in shape.
The Voltmeter measures the
This represents the part of the voltage drop across the
circuit where electrical energy resistive element.
It is connected in parallel
is consumed.
The resistive element could be It has a very high internal
resistance which diverts very
a light globe or heater or a
little current from the main
radio or a television.
circuit.
Resistive Element
V
Connecting Wires
Power
Supply
A
The Ammeter measures
current flow in the main
circuit.
It is connected in series
It has virtually no internal
resistance so as not to
interfere with the current in the
main circuit
Meters
17. A Galvanometer (which is a very sensitive ammeter) when included in a circuit
should be connected:
A: In parallel
B: Across the power supply
C: In series
D: Any way around, it doesn’t matter
18. In ideal circuits the wires used to connect the circuit components together have:
A: No resistance
B: A small amount of resistance
C: A large amount of resistance
D: An infinite amount of resistance.
19. Voltmeters and Ammeters differ because:
A: Voltmeters have low internal resistance and are connected in series while
Ammeters have high internal resistance and are connected in parallel.
B: Voltmeters have high internal resistance and are connected in parallel while
Ammeters have low internal resistance and are connected in series.
C: Voltmeters have low internal resistance and are connected in series while
Ammeters have high internal resistance and are connected in parallel.
D: Voltmeters have high internal resistance and are connected in series while
Ammeters also have high internal resistance and are also connected in series
Chapter 2
Resistance
2.0 Resistance
All materials fall into one of three categories as far as their electrical conductivity
is concerned.
ALL materials exhibit some opposition to currents
They are either :
flowing through them.
1. Conductors
2. Semiconductors, or Conductors show just a small amount of opposition.
Semiconductors show medium to high opposition.
3. Insulators
Insulators show very high to extreme opposition.
This opposition is called ELECTRICAL RESISTANCE.
The amount of resistance depends on a number of factors:
1. The length of the material.
2. The cross sectional area of the material.
3. The nature of the material, measured by Resistivity
Length = L
A1
Wire 1
Mathematically:
R = ρL/A
Where
R = Resistance in Ohms (Ω)
ρ = Resistivity in Ohm.Metres (Ω.m)
L = Length in Metres (m)
A = Cross Sectional Area in (m2)
A2
Wire 2
Wires 1 & 2 are made from the same material (ρ is
the same for each), and are the same length (L is
also the same).
Wire 1 has twice the cross sectional area of Wire 2.
Wire 1 has ½ the resistance of Wire 2
Resistance
20. Nichrome wire is sometimes used to make the heating elements in electric
kettles. It has a resistivity of 6.8 x 103 Ω.m. Calculate the resistance of a piece of
nichrome wire of length 1.2 m and cross sectional area 2 x 10-4 m2
R = ρL/A = (6.8 x 103)(1.2)/(2.0 x 10-4) = 4.1 x 107 Ω = 41 MΩ
21. Two pieces of wire are made of the same material and are of the same cross
sectional area. Wire 1 is 3 times as long as wire 2.
A: Wire 1 has 3 times the resistance of Wire 2
B: Wire 2 has 2/3 the resistance of Wire 1
C: Wire 1 has 1/3 the resistance of Wire 2
D: Wire 1 has 6 times the resistance of Wire 2
2.1 Resistors
Resistors are conductors whose
resistance to current flow has
been increased.
They are useful tools for
demonstrating the properties of
Electric Circuits.
Understanding how these
circuits work is an important
life skill you all need to
develop.
Resistor is a generic term
representing a whole
family of conductors such
as toaster elements, light
bulb filaments, bar
radiators and kettle
elements.
They are represented on circuit
diagrams as either,
1kΩ
or
1kΩ
There are only two ways to join resistors
together
IN SERIES:
The resistors are connected end to end
with only one path for the current to flow.
The more resistors the greater the overall
resistance
IN PARALLEL
The resistors are connected side by side
with more than one path for the current to
flow. The more resistors the lower the
overall resistance
2.2 Resistors in Series
Connected end to end, this combination of resistors gives only 1 path for
current flow.
I1
I2
I3
R1
RRT2
R3
V1
V2
V3
I
VS
The TOTAL
RESISTANCE (RT) of
this combination equals
the sum of resistances
Thus, RT = R1 + R2 + R3
In other words, the 3
resistors can be
replaced in the circuit
with a single resistor of
size RT
Because there is only 1
path for the current to flow,
the current must be the
same everywhere.
The current drawn from the
power supply (I) is equal to
the currents through the
resistors.
Thus I = I1 = I2 = I3
The sum of the Potential
Differences across the
resistors is equal to the
Potential Difference of
the supply
Thus VS = V1 + V2 + V3
Resistors in Series
24 Ω
21.(a) Calculate the equivalent resistance
that could replace the resistors in the circuit.
11
15 Ω
11 Ω
12
2.9
1.8
v3
I = 0.12 A
6.0
In series resistances add. RT = R1 + R2 + R3 = 24 + 15 + 11 = 50 Ω
(b) Determine the value of V3
In a series circuit VS = V1 + V2 + V3  V3 = VS – (V1 + V2) = 6.0 – (2.9 + 1.8) = 1.3 V
(c) Determine the values of I1 and I2
In a series circuit, current is the same everywhere so I1 = I2 = I = 0.12 A
2.3 Resistors in Parallel
When connected side by side, this combination of resistors (called a parallel
network) gives many paths for current flow.
The TOTAL RESISTANCE (RT) is calculated
from:
R1
I1
1/RT = 1/R1 + 1/R2 + 1/R3.
V1
In other words the three resistors can be
replaced by a single resistor of value RT.
I2 RRT2
The physical effect of this formula is that the
V2
value of RT is always less than the lowest
value resistor in the parallel network.
I3
R3
The current has many paths to travel and the
V3
total current drawn from the supply (I) is the sum
of the currents in each arm of the network.
I
Thus I = I1 + I2 + I3
VS
Each arm of the parallel network gets the full
supply Potential Difference.
Thus VS = V1 = V2 = V3
Resistors in Parallel
I = 12 mA
1 kΩ
22. (a) What single resistor could be used to
replace the 3 resistors in the circuit ?
I1
v3
3 kΩ
1/RE = 1/R1 + 1/R2 + 1/R3
= 1/1000 + 1/3000 + 1/12000
RE = 706 Ω
(b) Determine the values of V1, V2, and V3
In a parallel network VS = V1 = V2 = V3 = 12 V
(c) Determine the value of I1
In a parallel network I = I1 + I2 + I3
I1 = 17 – (12 + 1)
= 4 mA
I = 1.0 mA
v2
12 kΩ
v1
I = 17 mA
12V
Resistors Combined
23. (a) What single value resistor could
be used to replace the network shown ?
Simplify parallel networks first.
For 10 and 15, RE = (1/10 +1/15)-1
= 6.0 Ω.
For 50,50,100 RE = (1/50 + 1/50 + 1/100)-1
= 20 Ω.
Now
RE = 6 + 24 + 20
= 50 Ω
10 Ω
50 Ω
v1
50 Ω
15 Ω
24 Ω
3V
100 Ω
10 V
I = 0.5 A
25 V
(b) What is the Potential Difference across and the current through the 24 Ω
resistor ?
V24Ω = 25 – (10 + 3) = 12 V,
I24Ω = I = 0.5 A
2.4 Ohm’s Law
Conductors which obey Ohm’s Law
are called Ohmic Conductors.
Georg Ohm
1789 - 1854
The relationship between, the
potential difference across, the
current through, and the
resistance of, a conductor was
discovered by Georg Ohm and
is known as Ohm’s Law
Ohm’s Law stated
mathematically is:
V = IR
Where:
When expressed graphically, by
plotting V against I, Ohm’s Law
produces a straight line graph with a
slope equal to resistance (R)
V
Rise
Run
V = Potential Difference in Volts (V)
I = Current in Amps (A)
R = Resistance in Ohms (Ω)
Note the graph passes through the origin (0,0) as it must,
since if both V and I are zero, resistance is a meaningless
term.
Rise
Run = Slope
= Resistance
I
Ohm’s Law (1)
24. A current of 2.5 mA is flowing through a resistor of 47 kΩ. What is the
Potential Drop drop across the resistor ?
V = IR = (2.5 x 10-3)(4.7 x 104) = 117.5 V
25. A 12 V battery is driving a current through an 20 Ω resistor, what is
the size of the current flowing ?
V = IR  I = V/R = 12/20 = 0.6 amp
26. A resistor has a 48 V potential difference across it and a 2.4 A
current flowing through it. What is it’s resistance ?
V = IR  R = V/I = 48/2.4 = 20 Ω
Ohm’s Law (2)
R = 1.2 kΩ
27. What are the readings on meters V and A ?
V = VR = VSUPPLY = 12 V
I = VR/R = 12/(1.2 x 103) = 0.01 A
28. (a) Determine the value of the current measured
by ammeter A1 (express your answer in mA)
Need to find equivalent resistance by
simplifying parallel networks.
Simplify parallel networks first.
For 1.0k and 1.5k,
RE = (1/1000 +1/1500)-1
= 600 Ω.
For 500, 500, 1k;
RE = (1/500 + 1/500 + 1/1000)-1
= 200 Ω.
Now RE = 600 + 2400 + 200
= 3200 Ω
A1
= 3.2 k Ω
Now I = V/R = 25/3200
= 0.0078 A
= 7.8 mA
V
A
VP = 12 V
500 Ω
v2
1 kΩ
A2
500 Ω
1.5 kΩ
2.4 kΩ
V1
1 kΩ
v3
25 V
Ohm’s Law (3)
1 kΩ
(b) Determine the value of the potential
differences measured by voltmeters V1, V2
and V3.
500 Ω
v2
A2
500 Ω
1.5 kΩ
V1
2.4 kΩ
1 kΩ
V1 = Voltage across 1k, 1.5k combination.
v
RE = 600 Ω, so V1 = IRE
A1
= (7.8 x 10-3)(600)
= 4.68 V;
25 V
V2 = voltage across 2.4 kΩ
= (7.8 x 10-3)(2.4 x 103)
(c) Determine the current measured by
= 18.72 V;
ammeter A2
V3 = Voltage across the 500, 500, 1k
combination
A2 = current through 500 Ω resistor
= IRE
= V/R
-3
= (7.8 x 10 )(200)
= 1.56/500
= 1.56 V
= 3.12 x 10-3 A
3
2.5
Short Circuits
Short circuits occur when the
Resistive parts of a circuit are
bypassed, effectively connecting the
positive terminal of the power supply
directly to the negative terminal
providing a resistance free path for the
current.
The current immediately increases to its
maximum.
R2
This can be disastrous for the circuit
causing rapid heating and possibly a
fire.
This situation is taken care of by the use
of fuses, circuit breakers, “safety
switches”, or residual current devices.
(See chapter 5).
VS
Chapter 3
Non Ohmic Devices
3.0 Non Ohmic Conductors
Conductors which do not follow Ohm’s Law
are called Non Ohmic Conductors
Devices such as diodes and transistors can
be classed as non ohmics, but the best known
non ohmic is the incandescent light globe.
When a plot of Potential Difference against
Current is drawn, it is not a straight line.
A Typical “Characteristic Curve” for an Incandescent Light Globe
V
At High Voltages,
Slope is steep
= High Resistance
I
At Low Voltages,
slope is shallow
= Low Resistance
Non Ohmics - Series
29. Two non ohmic conductors with
“Characteristic Curves” as shown
opposite are connected in series in a
circuit as shown.
8
The voltage across device 1 is 6.0 V.
6
(a) What is the current through Device 2, 4
(b) What is the voltage across Device 2, 2
(c) What is the voltage of the battery
powering the circuit ?
Device 1
Device 2
Voltage (V)
Voltage (V)
8
6
4
Current (I)
1
2
2
Current (I)
1
2
6.0 V
Device 1
Device 2
(a) Voltage across device 1 = 6.0 V so current through device 1 = 0.5 A (read from
graph) because devices are in series current is same through both.
So I DEVICE 2 = 0.5
(a) Voltage across device 2 = 4.0 V (read up from 0.5 A on graph for device 2).
(b) VSUPPLY = Sum of voltage drops around the circuit = 6.0 + 4.0 = 10.0 V
Non Ohmics Parallel
30. Two devices with Characteristic
Curves” shown are connected in parallel.
The current through Device 1 is 1.0 A.
(a) What is the voltage across Device 2 ?
(b) What is the current through Device 2 ?
(c) What is the voltage of the battery ?
(d) the total current drawn from the
battery ?
1.5 A
Device 1
Device 1
Voltage (V)
Device 2
Voltage (V)
8
8
6
6
4
4
2
0
2
Current (I)
1
2
0
Current (I
1
2
Device2
(a) If current through device 1 = 1.5 A, then voltage across it = 8.0 V (read from
graph). In parallel network voltage is same across each member
so VDEVICE 2 = 8.0 V
(b) If voltage across device 2 = 8.0 V, current = 2.0 A (read from graph).
(c) VSUPPLY = VDEVICE 1 = VDEVICE 2 = 8.0 V
(d) Total Current = Sum of currents through each component = 1.5 + 2.0 = 3.5 A
Chapter 4
Cells & Batteries
4.0 Cells and Batteries
Electrical Cells (as opposed
to plant and animal cells) are
devices which perform two
functions:
1. Charge Separation.
2. Charge Energisation.
Charge Separation is the process of
separating positive and negative
charges to produce a POTENTIAL
DIFFERENCE capable of driving a
current around an external circuit.
Charge Energisation is the process of
providing the separated charges with the
ELECTRICAL ENERGY they need to
complete their journey around the circuit
connected to the cell.
A Single Cell
A group of Cells
ie. a Battery
Batteries have a limited ability to separate and energise
charge, they eventually go “flat”. See Slide 4.5
4.1 Power Supplies
Power Supplies, (as opposed to cells and
batteries) obtain their separated and energized
charges from the mains supply to which they
are connected, via the standard 3 pin plug.
They rely on the power generation company to
separate and energize the charge carriers at the
power station.
The power station remains “on line” at all times,
so the power supply can operate indefinitely,
i.e., it does not go “flat” like a battery.
In all other senses, power supplies behave in a similar
fashion to cells and batteries.
4.2 Electromotive Force (EMF)
Electromotive Force (EMF) is
not a true force in the
Newton’s Laws sense, but it
is a term used to describe the
OPEN CIRCUIT VOLTAGE of a
cell, battery or power supply.
EMF is represented by the
symbol (ε). The Greek letter
epsilon.
R
“Open Circuit” means that no
complete external circuit is
connected to the battery or power
supply and thus no current is
being drawn.
Consider the circuit shown
With the circuit complete, a current is flowing
and the P.D. across the power supply equals
the P.D. across the resistor.
With the switch open the current stops flowing,
the voltage across the resistor falls to zero and
the voltage reading across the power supply
rises.
The Voltage reading now is the EMF of the
supply
Cells and Batteries
31. The primary task of a battery or power supply is to:
A: Supply electrons and energise them
B: Provide energy for charge carriers
C: Provide charge separation and energization.
D: Separate electrons from protons.
32. The EMF of a battery or power supply is
A: The Potential Difference of the supply when a current is being drawn.
B: The Potential Difference of the supply when no current is being drawn
C: The Potential Difference difference between the positive and negative
terminals when they are short circuited.
D: The Potential Difference difference between earth and the positive
terminal.
33. When a battery or power supply is switched into an external circuit the
Potential Difference measured across the terminals of battery or power supply
will:
A: Fall because a current is now flowing
B: Rise because a current is now flowing
C: Remain unchanged even through a current is now flowing
D: None of these answers
4.3 Internal Resistance
The reason the Potential Difference
of the power supply falls when a
current is drawn from it is the
“Internal Resistance” of the
supply.
The internal resistance is:
•The “price which must be paid”
for drawing a current from the
supply.
•A measurable quantity and, as
with all resistance, is measured in
Ohms (Ω).
The larger the current drawn from
the supply, the greater the “cost”
(in terms of energy wasted inside
the supply), because of the internal
resistance.
This means less energy is available
for the charge carriers to flow
around an external circuit.
A cell, battery or power supply
can be represented as a pure
EMF in series with a resistor, r,
(representing the internal
resistance).
Power Supply
r
ε
V1
With no external circuit connected
(i.e. a so called “no load” situation),
no current is drawn from the supply,
and the voltmeter reading V1 will
equal ε, the EMF of the supply.
4.4 Internal Resistance
V2
The power supply now has an external circuit
connected.
This draws a current from the supply.
ε
This current also flows through the internal
resistance r.
This causes a potential difference = Ir across
R
that resistor.
The voltage measured by V2 will now be less (by an amount Ir) than the EMF
(ε) of the power supply.
r
I
Mathematically: V2 = ε - Ir
By replacing the fixed resistor (R) in the external circuit with a variable resistor,
and changing the value of the resistance, a set of values for V2 and the
corresponding current, I, can be obtained.
Plotting these values gives the following.
Voltage
(V2)
Intercept = ε
This method allows you to
calculate the internal
Slope = - r
resistance of the power
Current (I) supply, cell or battery.
Cells and Internal Resistance
34. A battery or power supply can be regarded as
A: A pure P.D. source in parallel with a resistance
B: A pure P.D. alone
C: A pure P.D. source in series with a resistor
D: A pure resistance in parallel with an EMF
35. A battery has an EMF of 9.0 V. When connected into a circuit drawing 25
mA the potential difference across the battery terminals in measured at 8.6
V. What is the internal resistance of the battery ?
V = ε – Ir
r = (ε – V)/I
= (9.0 – 8.6)/(2.5 x 10-2)
= 16 Ω
Internal Resistance
36. A group of students
set out to study the
properties of a D cell
battery. Using the
following circuit and
varying the resistance of
the rheostat they collected
the data shown.
V
2
I2
I
R
Voltage (v)
Voltage (V)
(volts)
Current (I)
(milliamps)
0.10
120
0.25
100
0.45
70.0
0.60
50.0
0.70
35.0
0.85
15.0
(b) EMF = y intercept = 0.95 V
1.0
(c) Internal resistance (r)
= negative of slope
= -(0.85 – 0.25)/(15 x 10-3 – 100 x 10-3)
= - (0.6)/(-75 x 10-3)
= 8Ω
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
10 20 3
0
40 5
0
60 7
0
8 9 100 110 120
0 0
Current (mA)
4.5 A Flat Battery
In a cell or battery, the
chemical processes used to
provide charge separation and
energisation become less
efficient as current is drawn
from it.
This shows up in an increase
in the Internal Resistance of
the battery.
The internal resistance will
continue to increase until the
battery is no longer able to
provide sufficient energy to
perform its primary task
(separation and energisation)
and the battery is said to be
flat.
In testing a battery with a
multimeter, you measure the EMF,
which may seem fine, because you
are not drawing a current from it.
To properly test a battery it needs
to be placed in a resistive circuit of
some kind so that a current is
drawn.
Measuring P.D. across the battery
now will now give a more realistic
picture of the battery’s condition.
Flat Battery
37. Explain why is not sufficient to simply measure the EMF of a battery to
check if it is “flat” ?
EMF does not measure the internal resistance of the battery and hence its
ability (or otherwise) to provide a current to external circuit.
Chapter 5
Fuses and Stuff
5.0 Fuses
Fuses are primarily
Safety Devices placed in
circuits to limit the
current flow to a certain
(predetermined) value.
Limiting the current in
this way reduces the
chance of fire caused by
overheating in a circuit
carrying excessive
current.
A Fuse is basically a
short piece of thin wire
which, when too much
current tries to flow
through it, overheats and
then melts, breaking the
circuit.
In the electricity supply
network fuses are
present throughout the
system and at the
domestic or household
end fuses are located in
the “Fuse Box ”
sometimes also called
the “Meter Box”.
Modern Meter Boxes
have resettable fuses
called “Circuit
Breakers” instead of
the old style porcelain
former with its separate
thin wire fuse.
5.1
Residual
Current
Interrupt
Increasingly, Meter Boxes contain
To understand the operation of the
Residual Current Interrupt Devices (RCI), RCI you need to know that a current
commonly called “safety switches” and in a wire causes a magnetic field
Surge Arrestors.
around that wire.
Both are safety devices.
The strength of the magnetic field
The RCI is designed to protect people
depends upon the size of the current.
while surge arrestors protect electrical
equipment.
THE RCI AND THE TOASTER
Active Wire
The RCI operates using two
coils to monitor the magnetic
fields produced by the
currents in both the active
and neutral wires.
Under normal conditions the
Active and Neutral currents
will be equal.
This means the induced
currents in the coils will also
be equal and will cancel one
another out inside the RCI.
Neutral Wire
RCI
G.P.O. or
Power point
Coils
Earth
If the two A and N currents are different, as
shown with some passing down the earth
wire, due to a short circuit in the toaster, the
RCI reacts by opening a switch in the active
wire, cutting off the current.
The RCI will respond in approx 0.03sec (less
than a heartbeat)
Safety
38. Which one or more of the following act as safety devices in electric
circuits ?
A: Fuses
B: Safety switches
C: Surge arrestors
D: Short Circuits
39. RCI’s monitor the currents in
A: The Neutral and Earth Lines
B: The Active and Earth Lines
C: The Active Line only
D: The Active and Neutral Lines
5.2
Switches
Switches break circuits by moving
Opening the switch (turning it “off”)
contacts apart.
isolates the power point from the
In the domestic situation switches
supply.
are always placed in the Active
If the switch was placed in the Neutral
Line.
line the power point would remain live
This is especially important for
even with the switch “off”
General Purpose Outlets (GPO’s)
There are large numbers and types of
more often called wall sockets or
switches in use. They can be
power points.
Mechanical, Electromechanical or
Electronic.
Sample Mechanical Switches are shown:
SPST
Single Pole, Single Throw
DPST
Double Pole, Single Throw
SPDT
Single Pole, Double Throw
DPDT
Double Pole, Double Throw
Switches
40. Identify each type of switch
Double Pole
Double Throw
Single Pole
Double Throw
Double Pole
Single Throw
Single Pole
Single Throw
5.3
Earthing
The Earth is a giant “sink” for electricity, it will soak up electric charge.
The name given to the process of connecting a circuit to the Earth is called
“earthing” and the physical connection is via the Earth Wire.
To better understand earthing, an understanding of domestic
wiring is needed. Below is a sample domestic wiring system
showing one power point only.
The Earth is also physically
Active Line
Neutral Line
connected to the neutral bar,
holding it at Earth potential
(voltage) of 0 volts.
Main Fuse
The Earth Wire provides a
“resistance free” path to
Meter
The earth
earth for any current that
stake is a
leaks from the active
Fuses
Main Switch
solid copper
and/or neutral lines.
piece driven
Meter Box Leaking current will
about 2 m into
choose to use the no (or
Neutral Bar
the ground
low) resistance path to
earth rather than the high
Power point
Earth Stake
resistance path through a
human.
Earthing, as used in domestic wiring, is just another safety feature.
5.4 Electric Shock
Electricity is dangerous! We
all know this, it was
drummed into us throughout
our childhood.
We can all remember the
reaction of adults the first
time they found us playing
with electrical sockets at
home.
But exactly how dangerous
is electricity and what does
it do to our bodies ?
The lowest recorded
voltage at which death
occurred was 32 V AC
Domestic electricity in
Australia is supplied at 240 V
AC, at 50 Hz. If you are
exposed to this supply for 0.5
sec and depending on the
size of the current, the
following effects will be
experienced.
Remember that 1 mA = 1/1000th of an Amp ( 1 mA = 1 x 10-3 A)
Current (mA)
1
3
10
20
50
90
150
200
500
Effect on Body
Able to be felt – slight tingling
Easily felt – distinct muscle contraction
Instantly painful - Cramp type muscle reaction
Instant muscle paralysis – can’t let go
Severe shock – knocked from feet
Breathing disturbed - burning noticeable
Breathing extremely affected
Death likely
Breathing stops – death inevitable
Chapter 6
Electricity
Consumption
6.0 Power Consumption
In general, POWER is defined as the time rate of doing WORK or the time
rate of ENERGY conversion.
Mathematically:
Where
P = W/t = E/t
P = Power (Watts)
W = Work (Joules)
E = Energy (Joules)
Rearranging the equation we wet:
t = time (secs)
E = P.t
so 1 Joule = 1 Watt.sec
The Joule is a very small unit, too small for the Energy companies to use
when it comes to sending out the bills to customers, so electricity is sold in
units called kilowatt hours. (kWh). Have a look at your own electricity bill at
home !
1 kW = 1000 W and 1 hour = 3600 s
So 1 kWh = 1000 x 3600 J
= 3.6 x 106 J
= 3.6 MJ.
Electric Power
41. An electricity bill indicates the household used 117.5 kWh of
electricity in a week. How many megajoules were used ?
1 kWh = 3.6 MJ so 117.5 kWh = (117.5)(3.6) = 423 MJ
42. What was the power consumption of the home (in Watts) ?
P = E/t, U = 423 MJ = 4.23 x 108 J
t = 1 week = 7 x 24 x 60 x 60 sec = 604800 s
P = E/t = (4.23 x 108)/(6.048 x 105) = 699 W
6.1 The Kilowatt Hour
A 100 W (0.1 kW) incandescent light globe which runs
for 1 hour consumes 0.1 x 1 = 0.1 kWh of electricity.
Cost to run @ 12c/kWh = 1.2 cents
A 1500 W (1.5 kW) electric kettle which boils
water in 5 minutes consumes 1.5 x 5/60 = 0.125
kWh of electricity.
Cost to run @ 12c/kWh = 1.5 cents
A 2000 W (2 kW) oven operating for 3 hours
consumes 2 x 3 = 6 kWh of electricity.
Cost to run at 12c/kWh = 72 cents
Domestic electricity costs between 12 cents and 20 cents a kWh
Running Costs
43. If domestic electricity costs 13.5 c per kWh. Calculate the cost of running
(a) a 100 W light globe run for 1 hr, (b) a 1500 W kettle run for 5 mins and (c) a
2 kW oven run for 3 hrs.
Light Globe = (0.1)(13.5) = 1.35 cents:
Kettle = (0.125)(13.5) = 1.69 cents:
Stove (6.0)(13.5) = 81 cents
6.2 Load Curves
The demand on the electricity supply is not constant:
•It varies from time to time during the day.
•It varies from day to day during the week.
•It varies from season to season during the year.
This variation is best displayed on a “Load Curve”
Blackouts or “Brownouts”
are likely at these times
12 Midnight
6 am
12 noon
12 Midnight
6 pm
100 %
Hot Day
Summer
Cold Day
Winter
75 %
Mild Day
Spring
50 %
Load Curves
Questions
44. Why does the demand on a hot summer day exceed the demand on a
cold winter’s day ?
Hot Summer days means use of air conditioners, the greatest consumers of
electrical power of all household appliances. In addition commercial air
conditioners must also work harder thus consuming more electricity.
45. “Blackouts”, loss of supply often occur when demand exceeds supply.
At what times and on what type of day are blackouts likely to occur ?
Just after noon and just after 6 pm on hot summer days
Ollie Leitl 2008