Download Chapter 12

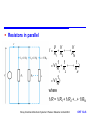
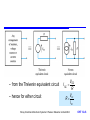
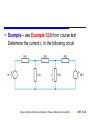
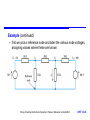
Resistance and DC Circuits
Chapter 12
 Introduction
 Current and Charge
 Voltage Sources
 Current Sources
 Resistance and Ohm’s Law
 Resistors in Series and Parallel
 Kirchhoff’s Laws
 Thévenin’s and Norton’s Theorems
 Superposition
 Nodal Analysis
 Mesh Analysis
 Solving Simultaneous Circuit Equations
 Choice of Techniques
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Introduction
12.1
 In earlier lectures we have seen that many circuits
can be analysed, and in some cases designed, using
little more than Ohm’s law
 However, in some cases we need some additional
techniques and these are discussed in this lecture.
 We begin by reviewing some of the basic elements
that we have used in earlier lectures to describe our
circuits
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Current and Charge
12.2
 An electric current is a flow of electric charge
I  dQ
dt
 At an atomic level a current is a flow of electrons
– each electron has a charge of 1.6  10-19 coulombs
– conventional current flows in the opposite direction
 Rearranging above expression gives
Q   Idt
 For constant current
Q  I t
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Voltage Sources
12.3
 A voltage source produces an electromotive force
(e.m.f.) which causes a current to flow within a circuit
– unit of e.m.f. is the volt
– a volt is the potential difference between two points
when a joule of energy is used to move one coulomb of
charge from one point to the other
 Real voltage sources, such as batteries have
resistance associated with them
– in analysing circuits we use ideal voltage sources
– we also use controlled or dependent voltage sources
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
 Voltage sources
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Current Sources
12.4
 We also sometimes use the concept of
an ideal current source
– unrealisable, but useful in circuit analysis
– can be a fixed current source, or a
controlled or dependent current source
– while an ideal voltage source has zero
output resistance, an ideal current source
has infinite output resistance
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Resistance and Ohm’s Law
12.5
 Ohm’s law
V I
– constant of proportionality is the resistance R
– hence
V
V
R
R
I
– current through a resistor causes power dissipation
V2
P
P  I 2R
P  IV
R
V  IR
I
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
 Resistors
– resistance of a given sample of material is determined
by its electrical characteristics and its construction
– electrical characteristics described by its resistivity 
or its conductivity  (where  = 1/)
R
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
l
A
OHT 12.‹#›
Resistors in Series and Parallel
12.6
 Resistors in series
V  IR  IR    IR
1
2
N
 I (R  R    R )
1
2
N
 IR
where
R = (R1 + R2+…+RN).
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
 Resistors in parallel
I  V  V  V
R R
R
1
2
N
 V( 1  1  1 )
R R
R
1
2
N
 V( 1)
R
where
1/R = 1/R1 + 1/R2 +…+ 1/RN
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Kirchhoff’s Laws
12.7
 Node
– a point in a circuit where two or more circuit components are joined
 Loop
– any closed path that passes through no node more than once
 Mesh
– a loop that contains no other loop
 Examples:
– A, B, C, D, E and F are nodes
– the paths ABEFA, BCDEB
and ABCDEFA are loops
– ABEFA and BCDEB are meshes
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
 Current Law
At any instant, the algebraic sum of all the currents
flowing into any node in a circuit is zero
– if currents flowing into the node are positive, currents
flowing out of the node are negative, then  I  0
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
 Voltage Law
At any instant the algebraic sum of all the voltages
around any loop in a circuit is zero
– if clockwise voltage arrows are positive and
anticlockwise arrows are negative then V  0
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Thévenin’s and Norton’s Theorems
12.8
 Thévenin’s Theorem
As far as its appearance from outside is concerned,
any two terminal network of resistors and energy
sources can be replaced by a series combination of an
ideal voltage source V and a resistor R, where V is the
open-circuit voltage of the network and R is the
voltage that would be measured between the output
terminals if the energy sources were removed and
replaced by their internal resistance.
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
 Norton’s Theorem
As far as its appearance from outside is concerned,
any two terminal network of resistors and energy
sources can be replaced by a parallel combination of
an ideal current source I and a resistor R, where I is
the short-circuit current of the network and R is the
voltage that would be measured between the output
terminals if the energy sources were removed and
replaced by their internal resistance.
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
– from the Thévenin equivalent circuit
– hence for either circuit
VOC
ISC 
R
V
R  OC
ISC
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
 Example – see Example 12.3 from course text
Determine Thévenin and Norton equivalent circuits of
the following circuit.
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Example (continued)
– if nothing is connected across the
output no current will flow in R2 so
there will be no voltage drop across
it. Hence Vo is determined by the
voltage source and the potential divider
formed by R1 and R3. Hence
– if the output is shorted to ground, R2 is
in parallel with R3 and the current taken
from the source is 30V/15 k = 2 mA.
This will divide equally between R2 and R3
so the output current, and so
– the resistance in the equivalent
circuit is therefore given by
30
V

 15 V
OC
2
ISC  1mA
R
VOC 15 V

 15 k
ISC 1 mA
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Example (continued)
– hence equivalent circuits are:
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Superposition
12.9
 Principle of superposition
In any linear network of resistors, voltage sources and
current sources, each voltage and current in the circuit
is equal to the algebraic sum of the voltages or
currents that would be present if each source were to
be considered separately. When determining the
effects of a single source the remaining sources are
replaced by their internal resistance.
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
 Example – see Example 12.5 from course text
Determine the output voltage V of the following circuit.
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Example (continued)
– first consider the effect of the 15V source alone
200 // 50
40
V  15
 15
 4.29 V
1
100  200 // 50
100  40
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Example (continued)
– next consider the effect of the 20V source alone
100 // 50
33.3
V  20
 20
 2.86 V
2
200  100 // 50
200  33.3
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Example (continued)
– so, the output of the complete circuit is the sum of these two voltages
V  V1  V2  4.29  2.86  7.15 V
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Nodal Analysis

12.10
Six steps:
1. Chose one node as the reference node
2. Label remaining nodes V1, V2, etc.
3. Label any known voltages
4. Apply Kirchhoff’s current law to each unknown node
5. Solve simultaneous equations to determine voltages
6. If necessary calculate required currents
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
 Example – see Example 12.8 from course text
Determine the current I1 in the following circuit
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Example (continued)
– first we pick a reference node and label the various node voltages,
assigning values where these are known
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Example (continued)
– next we sum the currents flowing into the nodes for which the
node voltages are unknown. This gives
50  V2
10

V3  V2
20

0  V2
15
V2  V3
0
20

100  V3
30

0  V3
25
0
– solving these two equations gives
V2 = 32.34 V
V3 = 40.14 V
– and the required current is given by
I1 
V3
25 

40.14 V
25 
 1 .6 A
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Mesh Analysis
12.11
 Four steps:
1. Identify the meshes and assign a clockwise-flowing
current to each. Label these I1, I2, etc.
2. Apply Kirchhoff’s voltage law to each mesh
3. Solve the simultaneous equations to determine the
currents I1, I2, etc.
4. Use these values to obtain voltages if required
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
 Example – see Example 12.9 from course text
Determine the voltage across the 10  resistor
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Example (continued)
– first assign loops currents and label voltages
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Example (continued)
– next apply Kirchhoff’s law to each loop. This gives
E  VA  VC  VF  VH  0
VC  VB  VD  VE  0
VF  VE  VG  VJ  0
– which gives the following set of simultaneous equations
50  70I1  20(I1  I 2 )  30(I1  I3 )  40I1  0
20(I1  I2 )  100I 2  80I 2  10(I3  I2 )  0
30(I1  I3 )  10(I3  I 2 )  60I3  90I3  0
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Example (continued)
– these can be rearranged to give
50  160I1  20I 2  30I3  0
20I1  210I 2  10I3  0
30I1  10I 2  190I3  0
– which can be solved to give
I1  326 mA
I 2  34 mA
I3  53 mA
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Example (continued)
– the voltage across the 10  resistor is therefore given by
VE  RE (I3  I 2 )
 10(0.053  0.034)
 0.19 V
– since the calculated voltage is positive, the polarity is as shown by
the arrow with the left hand end of the resistor more positive than the
right hand end
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Solving Simultaneous Circuit Equations
12.12
 Both nodal analysis and mesh analysis produce a
series of simultaneous equations
– can be solved ‘by hand’ or by using matrix methods
– e.g.
50  160I1  20I 2  30I3  0
20I1  210I 2  10I3  0
30I1  10I 2  190I3  0
– can be rearranged as as
160I1  20I 2  30I3  50
20I1  210I 2  10I3  0
30I1  10I 2  190I3  0
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Solving Simultaneous Circuit Equations
12.12
– these equations can be expressed as
160
-20
-30
I1
20
-210
10
I2
30
10
-190
I3
50
=
0
0
– which can be solved by hand (e.g. Cramer’s rule)
– or can use automated tools
 e.g. scientific calculators
 computer-based packages such as MATLAB or Mathcad
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Choice of Techniques
12.13
 How do we choose the right technique?
– nodal and mesh analysis will work in a wide range of
situations but are not necessarily the simplest
methods
– no simple rules
– often involves looking at the circuit and seeing which
technique seems appropriate
– see Section 12.3 of course text for an example
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›
Key Points
 An electric current is a flow of charge
 A voltage source produces an e.m.f. which can cause a
current to flow
 Current in a conductor is directly proportional to voltage
 At any instant the sum of the currents into a node is zero
 At any instant the sum of the voltages around a loop is zero
 Any two terminal network of resistors and energy sources
can be replaced by a Thévenin or Norton equivalent circuit
 Nodal and mesh analysis provide systematic methods of
applying Kirchhoff’s laws
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 12.‹#›