Download Currents and Kirchoff`s Laws

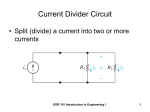
Circuits, Currents, and
Kirschoff’s Laws
A PROJECT BY JAMES SABO AND SALLY JUNE TRACY
VOLTAGE
ELECTRIC POTENTIAL
ENERGY DIFFERENCE
PER UNIT CHARGE
BETWEEN TWO POINTS
VOLTS (joules/coulomb)
CURRENT
MOVING ELECTRIC CHARGE
IS IN THE DIRECTION OF POSITIVE
CHARGE FLOW.
NET RATE AT WHICH CHARGE
CROSSES A GIVEN AREA
DRIVEN BY VOLTAGE DIFFRENCE
AMPERES (coulombs/second)
RESISTANCE
•
•
•
•
In most conductors charge doesn’t
move unimpeded
Charge looses energy gained from
electric potential difference in
collisions
This is described by the quantity of
resistance specific to different
conductors
In units of Ohms (volt meters)
V = IR
R1
I1
• The relationship
between voltage
current and resistance
• The potential drop
across a circuit
element is linearly
proportional to the
current
V = IR in Practice
• Lets suppose V1 = 6V
and R1 = 3Ώ
• V = IR  I = V/R
• I = (6V/ 3Ώ) = 2A
Kirschoff Loop Law
R1
V1
R2
• The sum of the voltages in
a circuit is equal to zero
• Across a resistor:
• With the current becomes
negative (voltage drop)
• Against the current
becomes positive (voltage
gain)
• V1 - I1R1 - I1R2 = 0
• Or
• I1R1 + I1R2 = V1
Kirschoff Node Law
• The sum of the
currents into and out
of a node are equal to
zero.
• Current in is positive
• Current out is negative
• I1 – I2 – I3 = 0
•  I1 = I2 + I3
Kirschoff’s Laws in Action
A
• As you can see, with
multiple voltage
sources and multiple
paths, V = IR will not
solve for the currents
here.
• Kirschoff’s laws must
be applied.
Apply Node Law
A
• At point A:
I1 + I2 - I3 = 0
• Or I1 + I2 = I3
• If the current direction is
not known, simply guess.
• Based on the circuit, it
looks like a good guess for
the direction of each, but
if we are wrong, don’t
worry! The current will
just become negative.
Apply Loop Law
Loop
Loop
1
2
• You can pick up to three
different loops here. The
two shown and one could
be picked around the
perimeter.
• From loop 1:
• V1 - I1R1 - I3R2 = 0
• From loop 2:
• V2 - I2R3 - I3R2 = 0
Solving the Circuit
• We have three equations and three
unknowns, the circuit can now be solved.
• WARNING, This section involves rigorous
algebra, you may become lost, confused or
bored in the process.
• Just bear with us it will be over soon
enough.
Solving the Circuit
•
•
•
•
•
•
•
•
•
From the three equations:
1. I1 + I2 = I3  I1 = I3 – I2
2. V1 - I1R1 - I3R2 = 0
3. V2 - I2R3 - I3R2 = 0
Sub 1. Into 2.
V1 – (I3 – I2)R1 - I3R2 = 0
Solve for I3.
4. I3 = (V1 - I2R1)/(R1 + R2)
Sub 4 into 3.
• V2 - I2R3 - [(V1 I2R1)/(R1 + R2)] R2 = 0
• Solve for I2
• I2 =[V2 – (V1R2)/(R1 +
R2)] / [(R3 – (R1R2)/(R1
+ R2)]
• Use given values:
• I2 = 1.20A
Still Solving the Circuit
•
•
•
•
•
•
•
Plug I2 into 4.
• As you can see that
method involves a lot
I3 = (V1 - I2R1)/(R1 + R2)
of algebra, and a lot of
I3 = 1.08A
keeping track of which
Sub I2 and I3 into 1
equation is where.
I1 = I 3 – I2
• Fortunately for us,
I1 = -.13A
there is a better way of
Now the circuit is
doing things.
solved!
Linear Systems…My Savior!
• You have seen before how currents can be
solved using rigorous algebra, but a much
simpler method can be used.
• Fortunately we are certain that anyone in
this class can solve this circuit using basic
row operations we have learned in this
class.
Use Linear Systems!
• Go back to the three
original equations.
• 1. I1 + I2 = I3
• 2. V1 - I1R1 - I3R2 = 0
• 3. V2 - I2R3 - I3R2 = 0
• Put all currents on the
left and all non
currents on the right.
• I1 + I 2 I3 = 0
• I1R1 +
I3R2 = V1
•
I2R3 + I3R2 = V2
• As you should be able
to see, this can become
a matrix.
• [ I 1 + I2 I3 : 0 ]
• [ I1R1 +
I3R2 : V1]
• [
I2R3 + I3R2: V2]
Taking the RREF
• An augmented matrix can
be formed.
• [1 1
-1 : 0 ]
• [ R1 0 R2 : V1]
• [ 0 R3 R2 : V2 ]
• Plug in the values
• [ 1 1 -1 : 0 ]
• [3 0 5:5 ]
• [ 0 8 5 :15 ]
• Find the RREF of the
matrix
• [ 1 0 0 : -.1265822]
• [ 0 1 0 : 1.202531 ]
• [ 0 0 1 : 1.075949 ]
• This corresponds to each
of the currents.
• I1 = -.1265822A
• I2 = 1.202531A
• I3 = 1.075949A
The Mesh Method
• A different form of Kirschoff’s loop laws to
solve for currents is called the Mesh
Method.
• Instead of assigning a current through each
resistor, assign a current through each loop.
• Once the currents are found, add the
currents flowing through each resistor.
Mesh Method Application
Loop
Loop
1
2
• Going back to the old
circuit we used, instead
of using three
equations (two loop
laws and a node law) It
can be broken into two
equations.
• V1 - I1R1 - (I1 + I2)R2 = 0
• V2 - I2R3 - (I2 + I1)R2 = 0
Mesh Method Application
• The currents can then be solved for in each
equation and put into a matrix.
• I1(R1 + R2) + I2R2 = V1
• I1R2 + I2(R3 + R2) = V2
• [ (R1 + R2)
R2
: V1 ]
• [ R2
(R3 + R2) : V2 ]
Mesh Method Application
• Plugging in original values, currents can be
solved. The currents through each resistor
are then added to solve for each current.
• [ (3Ώ + 5Ώ)
5Ώ
: 5V ] 
• [
5Ώ
(8Ώ + 5Ώ) :15V] 
• RREF =
•
[ 1 0 : -.1265822]
[ 0 1 : 1.202531 ]
[8 5 : 5]
[ 5 13 : 15]


I1 = -.1265822A
I2 = 1.202531A
Solving for the Currents
• We now know that
I1 = -.1265822A and that
I2 = 1.202531A
• Therefore the current
through R1 is I1= -.13A
The current through R3
is I2 = 1.20A and the
current through R2 is
(I1 + I2) = 1.07A
Why use the Mesh Method?
• You may wonder why the mesh method can
be helpful. In the last exercise, instead of 3
equations, there were 2. That doesn’t save
too much time.
• When the circuits start to get more tricky,
the mesh method starts to look a heck of a
lot more useful.
Monster Circuit
Six currents, which means six equations!
Quickly Analyze the circuit
• V3 - (I1 +I3)R3 - I1R6 - (I1-I2)R1 - V1 = 0
• V1 - (I2 - I1)R1 - I2R4 - (I2 + I3)R2 - V2 = 0
• V3 - (I1 + I3)R3 - I3R5 - (I2 + I3)R2 - V2 = 0
• I1(-R3 - R6 - R1) + I2(R1) + I3(-R3) =V1 - V3
• I1(R1) + I2(-R1 - R4 - R2) +I3(-R2) = V2 - V3
• I1(-R3) + I2(-R2) + I3(-R3 - R5 - R2) = V2 - V3
Put it in a matrix and take the
RREF
• [-R3 - R6 - R1
R1
-R3
: V1 - V3 ]
• [
R1
-R1 - R4 - R2
-R2
: V2 - V1 ]
• [
-R3
-R2
-R3 - R5 - R2 : V2 - V3 ]
•
•
•
•
Note that:
i1 = I2 - I1; i2 = -I2 - I3; i3 = I1 + I3
i4 = I2; i5 = I3; i 6 = I1 + I3
AND WE’RE DONE!
Thank you for paying
attention!
• We hope you all have a wonderful day and
that you have somewhat been enlightened in
the ways of linear systems!
• Goodbye