* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download No Slide Title
Power MOSFET wikipedia , lookup
Mechanical filter wikipedia , lookup
Josephson voltage standard wikipedia , lookup
Phase-locked loop wikipedia , lookup
Spark-gap transmitter wikipedia , lookup
Yagi–Uda antenna wikipedia , lookup
Superheterodyne receiver wikipedia , lookup
Power electronics wikipedia , lookup
Opto-isolator wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Operational amplifier wikipedia , lookup
Surge protector wikipedia , lookup
Crystal radio wikipedia , lookup
Distributed element filter wikipedia , lookup
Current mirror wikipedia , lookup
Current source wikipedia , lookup
Two-port network wikipedia , lookup
Electrical ballast wikipedia , lookup
Radio transmitter design wikipedia , lookup
Regenerative circuit wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Standing wave ratio wikipedia , lookup
Nominal impedance wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Rectiverter wikipedia , lookup
Index of electronics articles wikipedia , lookup
Network analysis (electrical circuits) wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
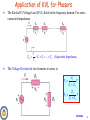
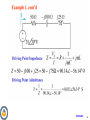
Chapter 9 Sinusoids and Phasors Phasor Relationships for circuit Elements. Impedance and Admittance. Kirchoff’s Laws in the Frequency Domain. Impedance Combinations. Applications. Huseyin Bilgekul EENG224 Circuit Theory II Department of Electrical and Electronic Engineering Eastern Mediterranean University EENG224 ‹#› Phasor Relationships for Circuit Elements After we know how to convert RLC components from time to phasor domain, we can transform a time domain circuit into a phasor/frequency domain circuit. Hence, we can apply the KCL laws and other theorems to directly set up phasor equations involving our target variable(s) for solving. Next we find the phasor or frequency domain equivalent of the element equations for RLC elements. EENG224 ‹#› Phasor Relationships for Circuit Elements i(t ) I m cos(t ) Re(Ie jt ) v(t ) i(t ) R RI m cos(t ) V RI m =RI Phasor voltage and current of a resistor are in phase Time Domain Frequency Domain EENG224 ‹#› Phasor Relationship for Resistor v(t ) i(t ) R RI m cos(t ) Frequency Domain V RI m =RI Voltage and current of a resistor are in phase Time Domain EENG224 ‹#› Phasor Relationships for Inductor di d v(t ) L L I m cos(t ) LI m sin(t ) LI m cos(t 90) dt dt V LI m ( 90)= LI m e j e j 90 j LI Phasor current of an inductor LAGS the voltage by 90 degrees. Time Domain Frequency Domain EENG224 ‹#› Phasor Relationships for Inductor Frequency Domain Phasor current of an inductor LAGS the voltage by 90 degrees. Time Domain EENG224 ‹#› Phasor Relationships for Capacitor dv d C Vm cos(t ) CVm sin(t ) CVm cos(t 90) dt dt I j j 90 I CVm ( 90)=CVm e e jCV V= jC i (t ) C Time Domain Phasor current of a capacitor LEADS Frequency Domain the voltage by 90 degrees. EENG224 ‹#› Phasor Relationships for Capacitor Frequency Domain Phasor current of a capacitor LEADS the voltage by 90 degrees. Time Domain EENG224 ‹#› Phasor Relationships for Circuit Elements EENG224 ‹#› Phasor Relationships for Circuit Elements EENG224 ‹#› Impedance and Admittance The Impedance Z of a circuit is the ratio of phasor voltage V to the phasor current I. V Z I or V =ZI The Admitance Y of a circuit is the reciprocal of impedance measured in Simens (S). I 1 Y or I =YV V Z Impedances and Admitances of passive elements. Element Impedance Admitance R Z=R L Z j L C Z= 1 j C 1 R 1 Y= j L Y= Y jC EENG224 ‹#› Impedance as a Function of Frequency The Impedance Z of a circuit is a function of the frequency. Element Impedance Admitance 1 L Z j L Y= j L 1 C Z= Y jC j C Inductor is SHORT CIRCUIT at DC and OPEN CIRCUIT at high frequencies. Capacitor is OPEN CIRCUIT at DC and SHORT CIRCUIT at high frequencies. Z L j L 0 (Short at DC) Z L (Open as ) ZL 0 1 j C Z C 0 (Open at DC) 0 ZC = ZC 0 (Open as ) EENG224 ‹#› Impedance of Joint Elements The Impedance Z represents the opposition of the circuit to the flow of sinusoidal current. V Z R jX I =Resistance + j Reactance = Z Z R X 2 R Z cos 2 Z + V I - X tan R X Z sin 1 The Reactance is Inductive if X is positive and it is Capacitive if X is negative. EENG224 ‹#› Impedance as a Function of Frequency As the applied frequency increases, the resistance of a resistor remains constant, the reactance of an inductor increases linearly, and the reactance of a capacitor decreases nonlinearly. Reactance of inductor versus frequency Reactance of capacitor versus frequency EENG224 ‹#› Z EENG224 ‹#› Admittance of Joint Elements The Admittance Y represents the admittance of the circuit to the flow of sinusoidal current. The admittance is measured in Siemens (s) Y + V I - 1 I Y G jB Z V Conductance + j Suseptance= Y 1 R jX R jX Y G jB 2 R jX R jX R X 2 R X G 2 B 2 2 R X R X2 EENG224 ‹#› Application of KVL for Phasors The Kirchoff”s Voltage Law (KVL) holds in the frequency domain. For series connected impedances: Z eq V Z1 Z 2 I Z N (Equivalent Impedance) The Voltage Division for two elements in series is: Z1 V1 V Z1 Z 2 Z2 V2 V Z1 Z 2 EENG224 ‹#› Parallel Combination for Phasors The Kirchoff”s Voltage Law (KVL) holds in the frequency domain. For series connected impedances: 1 I Yeq Y1 Y2 Zeq V 1 1 YN Z1 Z 2 1 (Eqiv. Admitance) ZN The Current Division for two elements is: I1 Z2 I Z1 Z 2 I2 Z1 I Z1 Z 2 EENG224 ‹#› Z3 Z1 EENG224 ‹#› EENG224 ‹#› Application of Current Division for Phasors EENG224 ‹#› Application of Current Division for Phasors EENG224 ‹#› Example EENG224 ‹#› EENG224 ‹#› EENG224 ‹#› Z1 EENG224 ‹#›