* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Physics 2102 Spring 2002 Lecture 8
Survey
Document related concepts
Transcript
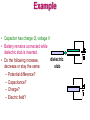
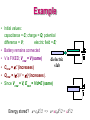
Physics 2102 We Are Borg. Resistance Is Futile! Jonathan Dowling Physics 2102 Lecture 13: WED 11 FEB Capacitors III / Current & Resistance Ch25.6–7 QuickTime™ and a decompressor are needed to see this picture. Ch26.1–3 QuickTime™ and a d eco mpres sor are nee ded to s ee this picture. Georg Simon Ohm (1789-1854) Exam 01: Sec. 2 (Dowling) Average: 67/100 A: 90–100 B: 80–89 C: 60–79 D: 50–59 Graders: Q1/P1: Dowling (NICH 453, MWF 10:30AM-11:30AM) Q2/P2: Schafer (NICH 222B, MW 1:30-2:30 PM Q3/P3: Buth (NICH 222A, MF 2:30-3:30 PM ) Q4/P4: Lee (NICH 451, WF 2:30-3:30 PM Solutions: http://www.phys.lsu.edu/classes/spring2009/phys2102/ Go over the solutions NOW. Material will reappear on FINAL! This problem from our slides first week of class. F (ii) (4 pts) What is the direction of the net electrostatic force on the central particle due to the other particles? F≠E! F≠E! Units! Most common mistake to Compute Magnitude and Direction of Electric Field instead of Electric Force at Central Point. This is Sample Problem from Book We worked on Board x F32 F13 q3 x–L Charges Alone Could Cancel to Left and To Right. Must discuss Big & Small Charge versus Small and Big Distance: Q vs. 1/r2 Common mistake: Wrong x. r r k q3 q1 k q3 q2 F31 F32 2 r31 r312 4kQ2 kQ2 4 1 2 2 2 2 x x x L x L Common mistake: To put q3 at –L to Left “By Symmetry” This would only make sense if q3 and q2 were held and q1 was free. But we are told q1 and q2 are fixed and q3 is free to move. So no symmetry! 4 x L x 2 2x L x 2 2x L x or 2x L x x 2L or x 2L /3 Not to right. Dielectric Constant • If the space between capacitor DIELECTRIC plates is filled by a dielectric, the capacitance INCREASES by a factor • This is a useful, working definition +Q –Q C = A/d for dielectric constant. • Typical values of are 10–200 The and the constant o are both called dielectric constants. The has no units (dimensionless). Atomic View Emol Molecules set up counter E field Emol that somewhat cancels out capacitor field Ecap. This avoids sparking (dielectric breakdown) by keeping field inside dielectric small. Ecap Hence the bigger the dielectric constant the more charge you can store on the capacitor. Example • Capacitor has charge Q, voltage V • Battery remains connected while dielectric slab is inserted. dielectric • Do the following increase, slab decrease or stay the same: – Potential difference? – Capacitance? – Charge? – Electric field? Example • Initial values: capacitance = C; charge = Q; potential difference = V; electric field = E; • Battery remains connected • V is FIXED; Vnew = V (same) • Cnew = C (increases) dielectric slab • Qnew = (C)V = Q (increases). • Since Vnew = V, Enew = V/d=E (same) Energy stored? u=0E2/2 => u=0E2/2 = E2/2 Summary • Any two charged conductors form a capacitor. • Capacitance : C= Q/V • Simple Capacitors: Parallel plates: C = 0 A/d Spherical : C = 4 0 ab/(b-a) Cylindrical: C = 2 0 L/ln(b/a) • Capacitors in series: same charge, not necessarily equal potential; equivalent capacitance 1/Ceq=1/C1+1/C2+… • Capacitors in parallel: same potential; not necessarily same charge; equivalent capacitance Ceq=C1+C2+… • Energy in a capacitor: U=Q2/2C=CV2/2; energy density u=0E2/2 • Capacitor with a dielectric: capacitance increases C’=kC What are we going to learn? A road map • Electric charge Electric force on other electric charges Electric field, and electric potential • Moving electric charges : current • Electronic circuit components: batteries, resistors, capacitors • Electric currents Magnetic field Magnetic force on moving charges • Time-varying magnetic field Electric Field • More circuit components: inductors. • Electromagnetic waves light waves • Geometrical Optics (light rays). • Physical optics (light waves) Resistance is NOT Futile! Electrons are not “completely free to move” in a conductor. They move erratically, colliding with the nuclei all the time: this is what we call “resistance”. The resistance is related to the potential we need to apply to a device to drive a given current through it. The larger the resistance, the larger the potential we need to drive the same current. Ohm’s laws V R i Units : [R] V and therefore : i and V iR R Volt Ohm (abbr. ) Ampere Georg Simon Ohm (1789-1854) "a professor who preaches such heresies is unworthy to teach science.” Prussian minister of education 1830 Devices specifically designed to have a constant value of R are called resistors, and symbolized by dq C i Ampere A s dt Current density and drift speed Vector : Same direction as E J such that i J dA The current is the flux of the current density! If surface is perpendicular to a constant electric field, then i=JA, or J=i/A [J ] Units: dA J Ampere m2 E i Drift speed: vd :Velocity at which electrons move in order to establish a current. Charge q in the length L of conductor: q (n A L) e L n =density of electrons, e =electric charge A t E i L vd i q n ALe n A e vd L t vd i J n Ae n e J n e vd vd Resistivity and resistance Metal “field lines” These two devices could have the same resistance R, when measured on the outgoing metal leads. However, it is obvious that inside of them different things go on. E resistivity: or, as vectors, E J J Resistivity is associated ( resistance: R=V/I ) m Ohm meter with a material, resistance with respect to a device 1 Conductivi ty : constructed with the material. Example: A - L V + V E , L i J A Makes sense! For a given material: V LRA i L A R L A Longer More resistance Thicker Less resistance Resistivity and Temperature Resistivity depends on temperature: = 0(1+a(T-T0) ) • At what temperature would the resistance of a copper conductor be double its resistance at 20.0°C? • Does this same "doubling temperature" hold for all copper conductors, regardless of shape or size? b Power in electrical circuits A battery “pumps” charges through the resistor (or any device), by producing a potential difference V between points a and b. How much work does the battery do to move a small amount of charge dq from b to a? a dW = –dU = -dq•V = (dq/dt)•dt•V= iV•dt The battery “power” is the work it does per unit time: P = dW/dt = iV P=iV is true for the battery pumping charges through any device. If the device follows Ohm’s law (i.e., it is a resistor), then V=iR and P = iV = i2R = V2/R