Download Lecture 1 - Digilent Inc.

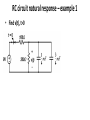
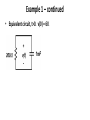
Lecture 16
(parts A & B)
•Inductors
•Introduction to first-order circuits
•RC circuit natural response
•Related educational materials:
–Chapters 6.4, 7.1, 7.2
Energy storage elements - inductors
• Inductors store
energy in the form
of a magnetic field
• Commonly
constructed by
coiling a conductive
wire around a
ferrite core
Inductors
• Circuit symbol:
• L is the inductance
• Units are Henries (H)
• Voltage-current
relation:
Inductor voltage-current relations
• Differential form:
• Integral form:
• Annotate previous slide to show initial
current, define times on integral, sketchy
derivation of integration of differential form to
get integral form.
Important notes about inductors
1. If current is constant, there is no
voltage difference across inductor
• If nothing in the circuit is changing
with time, inductors act as short
circuits
2. Sudden changes in current
require infinite voltage
• The current through an inductor
must be a continuous function of
time
Inductor Power and Energy
• Power:
• Energy:
t
1 2
 Li ( t )
2

Series combinations of inductors
+ v1(t) -
+ v2(t) +
vN(t)
-
Series combinations of inductors
• A series combination of inductors can be
represented as a single equivalent inductance
Þ
Parallel combinations of inductors
i1(t)
i2(t)
iN(t)
Þ
Example
• Determine the equivalent inductance, Leq
First order systems
• First order systems are governed by a first order
differential equation
• They have a single, first order, derivative term
• They have a single (equivalent) energy storage
elements
• First order electrical circuits have a single (equivalent)
capacitor or inductor
First order differential equations
• General form of differential equation:
• Initial condition:
Solutions of differential equations – overview
• Solution is of the form:
• yh(t) is homogeneous solution
• Due to the system’s response to initial conditions
• yp(t) is the particular solution
• Due to the particular forcing function, u(t), applied to the
system
Homogeneous Solution
• Lecture 14: a dynamic system’s response depends
upon the system’s state at previous times
• The homogeneous solution is the system’s response
to its initial conditions only
• System response if no input is applied Þ u(t) = 0
• Also called the unforced response, natural response, or
zero input response
• All physical systems dissipate energy Þ yh(t)0 as t
Particular Solution
• The particular solution is the system’s response to
the input only
• The form of the particular solution is dictated by the form
of the forcing function applied to the system
• Also called the forced response or zero state response
• Since yh(t)0 as t, and y (t) = yp(t) + yh(t):
• y (t) yp(t) as t
Qualitative example: heating frying pan
• Natural response:
• Due to pan’s initial
temperature; no input
• Forced response:
• Due to input; if qin is
constant, yp(t) is
constant
• Superimpose to get
overall response
• On previous slide, note steady-state response
(corresponds to particular solution) and
transient response (induced by initial
conditions; transition from one steady-state
condition to another)
RC circuit natural response – overview
• No power sources
• Circuit response is due
to energy initially
stored in the capacitor
v(t=0) = V0
• Capacitor’s initial
energy is dissipated
through resistor after
switch is closed
RC Circuit Natural Response
• Find v(t), for t>0 if the voltage across the capacitor before
the switch moves is v(0-) = V0
• Derive governing first order differential
equation on previous slide
• Talk about initial conditions; emphasize that
capacitor voltage cannot change suddenly
RC Circuit Natural Response – continued
• Finish derivation on previous slide
• Sketch response on previous slide
RC Circuit Natural Response – summary
• Capacitor voltage:
• Exponential function:
• Write v(t) in terms of :
•
•
•
•
Notes:
R and C set time constant
Increase C => more energy to dissipate
Increase R => energy disspates more slowly
RC circuit natural response – example 1
• Find v(t), t>0
Example 1 – continued
• Equivalent circuit, t>0. v(0) = 6V.