Download Resistors: In Series - McMaster University

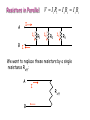
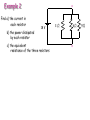
DC Circuits
•Series and parallel rules for resistors
•Kirchhoff’s circuit rules
“DC” Circuits
“Direct Current or DC”: current always flows in
one direction.
For circuits containing only resistors and emf’s the
current is always constant in time. Circuits containing
other elements such as capacitors and inductors as
well as resistors will have currents that change with
time.
Alternating current or AC is current that reverses
direction many times (eg: 60 Hz current in Canada) and
will not be treated in this course
Resistors in Series
R1
I
A
R2
V  IR
1
1
R3
V  IR
2
2
V  IR
3
B
3
We want to replace this combination by a single
resistor with resistance Reff
A
I
B
Reff
• Same current through all resistors
• Voltages add:
Veff = V1 + V2 + V3 + …
IReff = IR1 + IR2 + IR3 + …
So,
(same current through all)
Reff  R1  R2  R3  ...
Easy way to remember: think of the length of a string:
Ltot = L1 + L2 + L3 where L1 etc are the segments
Resistors in Parallel
1
1
2
2
I
A
I1
R1
I2
R2
I3
R3
I
B
V IR I R I R
We want to replace these resistors by a single
resistance Reff:
A
B
I
Reff
3
3
• Same voltage across each resistor
• Currents add:
Ieff = I1 + I2 + I3 +
V
V V V

 I eff  I1  I 2  I 3     ...
Reff
R1 R2 R3
1
1 1 1
    ...
Reff R1 R2 R3
Example 1
R1
11 V
R4
R3
R2
R5
All resistors = 1 Ω
Find: Effective resistance across the battery
R6
Quiz
Find the effective resistance of a network of
identical resistors:
A) 11/6 R
B) 6 R
C) 6/11 R
D) 1/6 R
R
R
R
R
R
R
Example 2
Find a) the current in
each resistor
b) the power dissipated
by each resistor
a
18 V
c) the equivalent
resistance of the three resistors
3Ω
6Ω
b
9Ω
Example 3
A regular “40 watt” bulb and a “60 watt” bulb are
connected in SERIES across 120 V.
What power does each bulb give? (Assume that the
resistances don’t change with temperature—these
are special bulbs.)
Kirchhoff’s Circuit Rules
Junction Rule: total current in = total current out
at each junction (from conservation
of charge).
Loop Rule: Sum of potential differences around any
closed loop is zero (from conservation of energy).
Charge q moves through circuit changing its potential
energy qV but eventually there is no overall change.
Junction Rule: conservation of charge.
I1
I2
I1 = I2 + I3
I3
Sum of currents entering a junction equals the sum of
currents leaving the junction
Alternately:
I1
I2
I1 = I2 + (I1-I2)
I1-I2
Loop Rule: conservation of energy.
Follow a test charge q around a loop:
 (V )  0

i
R
I
-
+

-Q
+Q
around any loop in circuit.
ΔV = -IR
ΔV =

ΔV = Q/C
C
loop
loop going from left to right
Example 5
A dead battery is charged by connecting it to the live
battery of another car with jumper cables. Determine the
current in the starter and in the dead battery.
Solution
Example
In the circuit shown, currents of 2.50 A and 1.60 A flow
in the branches indicated in the diagram. Apply
Kirchhoff’s circuit rules and calculate the potential
difference VeVb between points b and e in the diagram.
2.5 A
2.0 
c
3.0 
d
I2
I1
R

e
b
4.0 
2.5 A
I3
a
1.6 A
6.0 
f