Download Document

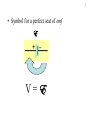
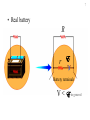
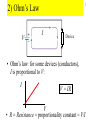
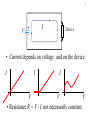
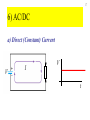
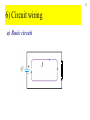
1
Chapter 20
Circuits
2
1) Electric current and emf
a) Potential difference and charge flow
Battery produces potential difference causing
flow of charge in conductor
3
b) Current:
I = Dq/Dt
∆ q is charge that passes the surface in time ∆ t
Units: C/s = ampere = A
4
• Drift velocity: average velocity of electrons
~ mm/s
• Signal velocity: speed of electric field
= speed of light in the material ~108 m/s
5
c) Electromotive force, emf
battery
E
is like
gh
gravitational analogy for a circuit
• emf = electromotive force = maximum potential
difference produced by a device
• Symbol: E
• emf is not a force, but it causes current to flow
6
• Symbol for a perfect seat of emf
E
V=E
7
• Real battery
R
E
r
Battery terminals
V < E in general
8
2) Ohm’s Law
V
I
Device
• Ohm’s law: for some devices (conductors),
I is proportional to V:
I
V = IR
V
• R = Resistance = proportionality constant = V/I
9
I
V
Device
• Current depends on voltage and on the device
I
I
I
V
V
V
• Resistance R = V / I, not necessarily constant
10
V
I
Device
• Ohmic material obeys Ohm’s Law: R is constant
• R is a property of the device
• symbol:
3) Resistivity
11
a) Definition
• Property of material; zero for superconductors
• For cylindrical conductor:
A
• R is proportional to L
L
• R is proportional to 1/A
• R is proportional to L / A
• Define resistivity  as the proportionality constant
L
R
A
12
b) values
• Conductors: ~ 10-8 Wm (Cu, Ag best)
• Semiconductors: ~ 1 - 103 Wm (Ge, Si)
• Insulators: ~ 1011 - 1016 Wm (rubber, mica)
13
c) Temperature dependence
• Resistivity is linear with temperature:

a  bT0
  0  b(T T 0)
  a  bT
0  resistivity at T  T0

 / 0  1 (TT 0)
  coefficient of resistivity (C º
  0 (1 (T T
))
0

 R  R0 (1 (T T 0))
-1
)
For metals,  > 0 (resistance increases with temp)
For semiconductors,  < 0 (resistance decreases)

14
d) Superconductors
• Below critical temp Tc,  –> 0
– Current flows in loop indefinitely
– Quantum transitions not possible
Tc typically < 10 K, but can be > ~ 75 K (high Tc ceramics)
(record is 138 K)
Applications: MRI, MagLev trains
15
4) Power and Energy
a) Power dissipated in a device
I
V
• Energy lost or gained by Dq is DUDqV
• Power:
DU
DqV
P
Dt

Dt
P  VI
Units: (C/s)(J/C) = J/s = W
Consumed energy = P t: [kW h] = (1000 W) (3600 s) = 3.6 MJ



16
b) Power dissipated in resistors
I
V
P  VI  (IR)I 
V


V
P

VI


R

V = IR
PI R
2
2
V
P
R
17
6) AC/DC
a) Direct (Constant) Current
V
I
V
t
18
b) Alternating Current
V
V0
I
QuickTime™ and a
TIFF (Uncompressed) decompressor
are needed to see this picture.
V
-V0
ac generator alternates polarity:

e.g. V  V0 sin( t)
t
19
V0
Average voltage: zero
V
V0
Vrms  V 
2
t
-V0
I0
2
Average current: zero

I
I0
Irms  I 
2
t
-I0
2
For resistors
Average power:
P  12 V0I0

V0 I0
 VrmsIrms
P
2 2

20
6) Circuit wiring
a) Basic circuit
E
I
21
b) Ground
One point may be referred to as ground
E
I
=
E
The ground may be connected to “true”
ground through water pipes, for example.
I
22
c) Short circuit
E
d) Open circuit
E
I
23
e) Series connection
same current
I
f) Parallel connection
V
same voltage
24
7) Resistors in series
For perfect conductors
V  V1  V2
From Ohm’s law

V1  IR1 and V2  IR2
So, V  IR1  IR2  I(R1  R
2)
Or, V  IRS

if
RS  R1  R2
25
Find the current and the power through each resistor.
In general, for series resistors,
RS  R1  R2  R3 L
RS   Ri
i
26
Voltage divider
Current is the same in both resistors
V
V
 1A
I

RS R1  R2
I
V=10V
R1=6W
R2=4W

Voltages divide in proportion to R
V1  IR1 6V
Vo
V2  IR2  4V

Output Voltage:

V
 R2 
R2  V 
Vo  IR2 

R1  R2
R1  R2 
V
Vo
27
8) Resistors in parallel
a) General case
Conservation of charge
I  I1  I2
Ohm’s Law

So,
V  I1R1 and
V V
 1
1 
I

 V   
R1 R2
R1 R2 

Or, V  IRP

if
1
1
1


RP R1 R2
V  I2R2
1
1
1


RP R1 R2


R1R2
RP 
 R1 //R2
R1  R2

• Equivalent resistance is smaller than either R1 or R2
• Conductance adds
In general, for parallel resistors,
or
1
1

RP
i Ri
1
1
1
1



L
RP R1 R2 R3
28
29
conductance adds
30
parallel connections in the home
31
b) Special cases
i) Equal resistance
R
R2

RP  R // R 
2
2R
ii) Very unequal resistors
(e.g. 1W and
1 MW

R1R2
(1)(10 6 )W
RP  R1 // R2 

 1W
6
R1  R2
1  10
If R2  R1, then R1  R2  R2
R1R2

so RP 
 R1
R2
RP = the smaller value