Download Electric Current

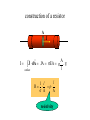
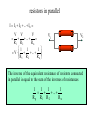
Electric (conduction) current
a) Transport of charge;
+
+
+
+
+
-
+
+
-
-
-
-
+
I
I
b) The electric current across a surface is defined as the rate at
which charge is transferred through this surface.
dQ
I
dt
According to general agreement its direction is chosen to coincide with the
direction in which positive charge carriers would move, even if the actual
carriers have a negative charge.
The SI unit of current is 1A (ampere). (1C=1A1s.)
drift velocity
 
The average velocity, v d r , of charge carriers over a

differential vicinity of a given location r is called the drift
velocity at this location.
1 

v d   vi
N i
drift velocity
The center of charge enclosed in this volume moves with the drift velocity.

drcq



d 1
q
dri


 qri  
  vd
dt  Nq i 1  Nq i dt
dt
N
current density

The current density J (associated with one type of charge
carriers) is defined as a product of the drift velocity, the
concentration of charge carriers and the charge of the carriers:


J  nqvd
current density and current
Current through a surface is equal to the flux of current density
over that surface.
The charge transferred through a differential
surface dA in time dt


dq  nq c  dV  nq c  dt  v d  dA  

 nq c  dA  v d dt  cos   dt  J  dA
vd

The charge dQ transferred though the entire surface in time dt
 
dQ   dq  dt   J  dA
surface
the current through the surface
I
surface
 
 J  dA
surface
dA
n
dQ = ?
vddt
electric current in a conductor
In a conductor, current density is proportional to the electric
field vector


J  E
(Ohm's law)
The constant of proportionality  is called the conductivity
of the conductor.
I
Under a steady flow of charged particles
along a conductor, the current across any
cross section of the conductor has the
same value.
We assign this value to the current in the
conductor.
I
I
resistor
A resistor is an electrical element with two sides for which (at
any instant) the current passing through this element (any
cross section) is proportional to the potential difference
between its terminals.
I
Vb
Va
Va – Vb = IR
R
The proportionality coefficient R is called the resistance of the resistor.
In SI 1 is the unit of resistance (1=1V/1A).
construction of a resistor
A 
J
 
A
I   J  dA  JA  EA    V
l
surface
l
1 l
 
R 
A
 A
resistivity
effect of temperature
In a relatively wide range of temperatures the resistivity of a
material is a linear function of temperature:
 = 0 [1 + (T-T0)]
resistivity
The proportionality coefficient  is called the temperature
coefficient of resistivity.
metals
semiconductors
temperature
resistors in series
Vb
Vz
dQ
I
Va
dQ
I
V  Vz  Va  Vb  Va   Vc  Vb   ...Vz  Vy  
 IR1  IR 2  ...  IR n  I(R1  R 2  ...  R n )
Equivalent resistance of resistors connected in series is
equal to the sum of the resistances of all resistors
Rs = R1 + R2 + … + Rn
resistors in parallel
I  I1  I2  ...  In 
V V
V


 ... 

R1 R 2
Rn
 1
1
1 

 V   
 ... 
Rn 
 R1 R 2
V1
V2
The inverse of the equivalent resistance of resistors connected
in parallel is equal to the sum of the inverses of resistances
1
1
1
1


 ... 
R p R1 R 2
Rn
electric power
The rate at which the electric field performs work on the
charged particles is called the electric power.
V1
dq
I
V2
dq
dWel  dq  (V2  V1 )
 I t   V  t 

Pt  
dt
dt
The electric power delivered to an electrical
element at instant t is equal to the product of
the current flowing through this element and
the voltage across this element at this
instant.
electric power dissipated in a resistor
V2
V1
P  t   I t   V  t 
dQ
I
From Ohm's law (which is satisfied by all resistors) the
electric power dissipated in a resistor can be determined
Veither the current
also if the resistance of the resistor Iand

V

IR
through or the voltage across the resistor R
is known.
2
V
P  I 2 R
V  IV
R