Download Methods of Analysis

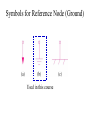
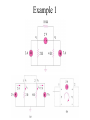
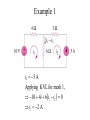
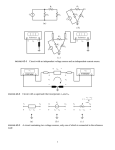
Methods of Analysis
Instructor: Chia-Ming Tsai
Electronics Engineering
National Chiao Tung University
Hsinchu, Taiwan, R.O.C.
Contents
•
•
•
•
•
•
•
Introduction
Nodal Analysis
Nodal Analysis with Voltage Sources
Mesh Analysis
Mesh Analysis with Current Sources
Nodal Analysis vs. Mesh Analysis
Applications
Introduction
• Nodal Analysis
– Based on KCL
• Mesh Analysis
– Based on KVL
• Linear algebra is applied to solve the
resulting simultaneous equations.
– Ax=B, x=A-1B
Nodal Analysis
• Circuit variables = node voltages
• Steps to determine node voltages
– Select a reference node, assign voltages v1, v2,…,
vn-1 for the remaining n-1 nodes
– Use Ohm’s law to express currents of resistors
– Apply KCL to each of the n-1 nodes
– Solve the resulting equations
Symbols for Reference Node (Ground)
Used in this course
Case Study
Applying Ohm' s law gives
v1  0
i1 
or i1  G1v1
R1
i2 
v1  v2
R2
or i2  G2 v1  v2 
i3 
v2  0
R3
or i3  G3v2
At node 1, applying KCL gives
I1  I 2  i1  i2
 I1  I 2  G1v1  G2 v1  v2 
At node 2, applying KCL gives
I 2  i2  i3
 I 2  G2 v1  v2   G3v2
G1  G2

  G2
 G2   v1   I1  I 2 




G3  G3  v2   I 2 
Assign vn
Nodal Analysis with Voltage Sources
• If a voltage source is connected
between a nonreference node
and the reference node (or
ground)
– The node voltage is defined by
the voltage source
– Number of variables is reduced
– Simplified analysis
Continued
• If a voltage source is
connected between two
nonreference nodes
– The two nodes form a
supernode
– Apply KCL to the supernode
(similar to a closed boundary)
– Apply KVL to derive the
relationship between the two
nodes
Supernode
Case Study with Supernode
v1  10 V
(1)
Applying KCL to the supernode,
 i1  i4  i2  i3
v1  v2 v1  v3

2
2
v2  0 v3  0


(2)
2
2
Applying KVL to the supernode,

 v2  v3  5
(3)
3 variables solved by 3 equations
Example 1
Example 2
What is a mesh?
• A mesh is a loop that does not contain any
other loop within it.
Mesh Analysis
• Circuit variables = mesh currents
• Steps to determine mesh currents
–
–
–
–
Assign mesh currents i1, i2,…, in
Use Ohm’s law to express voltages of resistors
Apply KVL to each of the n meshes
Solve the resulting equations
Continued
• Applicable only for planar circuits
• An example for nonplanar circuits is shown
below
Case Study
For mesh 1, applying KVL gives
 V1  R1i1  R3 i1  i2   0
 R1  R3  i1  R3i2  V1
For mesh 2, applying KVL gives
R2i2  V2  R3 i2  i1   0
  R3i1  R2  R3  i2  V2
 R1  R3

  R3
 R3   i1   V1 




R2  R3  i2   V2 
Mesh Analysis with Current Sources
• If a current source exists only in one mesh
– The mesh current is defined by the current
source
– Number of variables is reduced
– Simplified analysis
Continued
• If a current source
exists between two
meshes
– A supermesh is
resulted
Excluded
– Apply KVL to the
Supermesh
supermesh
– Apply KCL to derive
the relationship
between the two mesh
i2  i1  I S
currents
Example 1
i1  i2
i2  5 A
Applying KVL for mesh 1,
 10  4i  6i1  i2   0
 i1  2 A
Example 2
Supermesh
Applying KVL to the supermesh,
 20  6i1  10i2  4i2  0
Applying KCL to node 0,
 i2  i1  6
 6i1  14i2  20
 i1  3.2 A, i2  2.8 A
Example 3
Supermesh
•
•
•
•
Applying KVL to the supermesh
Applying KCL to node P
Applying KCL to node Q
Applying KVL to mesh 4
4 variables solved
by 4 equations
How to choose?
• Nodal Analysis
– More parallel-connected elements, current
sources, or supernodes
– Nnode < Nmesh
– If node voltages are required
• Mesh Analysis
– More series-connected elements, voltage
sources, or supermeshes
– Nmesh < Nnode
– If branch currents are required
Applications: Transistors
• Bipolar Junction Transistors (BJTs)
• Field-Effect Transistors (FETs)
Bipolar Junction Transistors (BJTs)
• Current-controlled devices
I E  I B  IC
(KCL)
VCE  VEB  VBC  0 (KVL)
VBE  0.7 V
IC   I B
(  ~ 100)
IC   I E
(0    1)
I E  1    I B


1
DC Equivalent Model of BJT
Example of Amplifier Circuit