* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Demonstration of Using Flywheels and FACTS Control for Transient Stabilization and
Power factor wikipedia , lookup
Three-phase electric power wikipedia , lookup
Control theory wikipedia , lookup
Pulse-width modulation wikipedia , lookup
Audio power wikipedia , lookup
Wireless power transfer wikipedia , lookup
Grid energy storage wikipedia , lookup
Electrical substation wikipedia , lookup
Buck converter wikipedia , lookup
Power over Ethernet wikipedia , lookup
Resilient control systems wikipedia , lookup
Electrification wikipedia , lookup
Control system wikipedia , lookup
History of electric power transmission wikipedia , lookup
Electric power system wikipedia , lookup
Variable-frequency drive wikipedia , lookup
Intermittent energy source wikipedia , lookup
Voltage optimisation wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Power electronics wikipedia , lookup
Life-cycle greenhouse-gas emissions of energy sources wikipedia , lookup
Mains electricity wikipedia , lookup
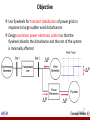
Demonstration of Using Flywheels and FACTS Control for Transient Stabilization and Interactions with Transactive Energy Market Kevin Bachovchin Milos Cvetkovic Martin Wagner [email protected] Carnegie Mellon University [email protected] Massachusetts Institute of Technology [email protected] Carnegie Mellon University 10th CMU Electricity Conference April 1, 2015 Joint work with Prof. Marija Ilic [email protected] Outline Motivation for fast control Transient stabilization using flywheel energy storage systems Competitive control; cancel effect of wind disturbance Demo on the Smart Grid in a Room Simulator (SGRS) Interaction of flywheel control with transactive energy market Transient stabilization using FACTS devices Cooperative control logic based on ectropy Implications for SGRS numerical integration 2 Motivation for Fast Control Transactive energy control is a steady-state scheduling concept Does not guarantee dynamic stability Interest in implementing more renewable energy sources into future power grids Renewables introduce more uncertainty, intermittency and unpredictability => a challenge for control design Large sudden deviations in wind power can cause high deviations in frequency and voltage transient instabilities Possible solution: fast energy storage flywheel energy storage systems FACTS devices 3 Objective Use flywheels for transient stabilization of power grids in response to large sudden wind disturbances Design nonlinear power electronic control so that the flywheel absorbs the disturbance and the rest of the system is minimally affected P P P P 4 Variable Speed Drives for Flywheels Use AC/DC/AC converter to regulate the speed of the flywheel (and hence the energy stored) to a different frequency than the grid frequency Controllable inputs are the switch positions in the power electronics Source: K. D. Bachovchin, M. D. Ilic, "Transient Stabilization of Power Grids Using Passivity-Based Control with Flywheel Energy Storage Systems," IEEE Power & Energy Society General Meeting, Denver, USA, July 2015.. 5 Controller Implementation Time-scale separation to simplify the control design Regulate both the flywheel speed and the currents into the power electronics using nonlinear passivity-based control Source: K. D. Bachovchin, M. D. Ilic, "Transient Stabilization of Power Grids Using Passivity-Based Control with Flywheel Energy Storage Systems," IEEE Power & Energy Society General Meeting, Denver, USA, July 2015.. 6 Transient Stabilization Using Flywheels P P P P Want to choose set points so that the wind disturbance power goes to the flywheel and rest of the system is minimally affected 7 Simulation Results: Flywheel Since the power output of the wind generator decreases during the disturbance, the flywheel set point decreases Wind Generator Mechanical Torque Flywheel Speed angular velocity(rad/sec) 0.26 torque(N*m) 0.255 0.25 0.245 0.24 0.235 0.23 0 0.2 0.4 time(sec) 0.6 0.8 1290 1280 ref 1270 1260 1250 1240 1230 0 0.2 0.4 time(sec) 0.6 0.8 8 Simulation Results: Power Electronics The set points for the power electronic currents are chosen so that the total current out of Bus 2 remains constant during the disturbance Power Electronic and Wind Currents Power Electronic Currents 2.4 current(A) current(A) -251 -252 i1d -253 -254 iref 1d 0.2 0.4 0.6 1.8 0 0.8 0.2 0.4 0.6 0.8 20.02 36 i1q 35 iref 1q current(A) current(A) 2 1.6 0 37 34 33 i1d+iSdW 2.2 0 0.2 0.4 t(sec) 0.6 0.8 i1q+iSqW 20.01 20 19.99 19.98 0 0.2 0.4 t(sec) 0.6 0.8 9 Simulation Results: Rest of System With the control, the effect on the rest of the system is very minimal and lasts only a short time 0.0745 voltage(V) 0.066 voltage(V) Bus 2 Voltage: Direct Component Bus 1 Voltage: Direct Component Vd (Control) Vd (No Control) 0.065 0.064 0.2 0.4 0.6 Vq (Control) Vq (No Control) 0.2 0.4 t(sec) 0.6 0.2 0.4 0.6 0.8 2 0.8 Vq (Control) 1.995 1.99 0 0 Bus 2 Voltage: Quadrature Component voltage(V) voltage(V) 0.073 2.005 2 1.995 Vd (No Control) 0.0735 0.8 Bus 1 Voltage: Quadrature Component 1.99 0.074 0.0725 0 Vd (Control) Vq (No Control) 0 0.2 0.4 t(sec) 0.6 0.8 10 Linking Multi Time-Scale Simulations Communication for multi time-scale simulation with ALM and fast dynamics for generators Source: M. R. Wagner, K. D. Bachovchin, M. D. Ilić, "Computer Architecture and Multi Time-Scale Implementations for Smart Grid in a Room Simulator," EESG Working Paper No. R-WP-1-2014, March 2015. 11 Importance of Reactive Power Typically the market only specifies the active power set point However the reactive power is critically important to the equilibria and stability of the system Power Factor PF = 0.99 (Without Shunt Capacitor) Power Factor PF=0.2 (Without Shunt Capacitor) 3 3 Manifold of Active Power Balancing Eqn at Bus 2 Manifold of Active Power Balancing Eqn at Bus 2 Manifold of Reactive Power Balancing Eqn at Bus 2 2 2 [0.9615, -0.18 rad] 1 2 (rad) 2 (rad) 1 0 0 -1 -1 [0.182, -1.27 rad] -2 -2 -3 -3 0 0.5 1 1.5 2 2.5 3 Voltage V2 (pu) 3.5 4 4.5 5 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 Voltage V2 (pu) Source: X. Miao, K. D. Bachovchin, M. D. Ilić, "Effect of Load Type and Unmodeled Dynamics in Load on the Equilibria and Stability of Electric Power System," EESG Working Paper No. R-WP-1-2014, March 2015. 12 5 Flores Island – Market Based on prices, market computes active power set points P* from each component 13 Flores Island – Dynamics Since currently the market does not specify reactive power set points Q*, data for Q* is randomly created Place a voltage source inverter and the variable speed drive on the hydro and diesel generator buses Control the sum of the power out of the hydro and diesel generators to match the active and reactive power set points 14 Simulation Results – Combining Dynamics and ALM Unstable Case: Reactive Power Load Consumption 10 5 0 0 20 40 60 80 100 power(pu) power(pu) Stable Case: Reactive Power Load Consumption 10 5 0 0 20 40 80 100 t(min) t(min) Wind Generator Bus Voltages Wind Generator Bus Voltages 1.2 1.2 1 1 0.8 vB2d vB2q 0.6 0.4 voltage(V) voltage(pu) 60 0.8 vB2d 0.6 vB2q 0.4 0.2 0 0.2 -0.2 0 -0.2 -0.4 0 20 40 60 t(min) 80 100 -0.6 0 20 40 60 t(min) 80 15 100 Transient Stabilization of Interactions Using FACTS Implications for SGRS distributed integration of differential equations Large scale interconnected power system Transient stability problem • • • Nonlinear dynamics Multiple time scales Large regions Unstable Stable Interactions are captured using an energy-based model • • Accumulated energy as a measure of stability Managing energy to ensure stability Cooperative power electronics (FACTS) control • Fast thyristor switching • Flow control Common Modeling Approach for FACTS Control Create a simplified power system model Control logic is case dependent Loaded as test case for transients simulator Create a structure preserving system model by combining dynamic models of individual components Coupling achieved through states on ports of components 𝑦𝑖 , 𝑝𝑖 Competitive control design Module description 𝑥𝑖 = 𝑓𝑖 𝑥𝑖 , 𝑦𝑖 , 𝑢𝑖 , 𝑑𝑖 𝑦𝑖 = 𝑦𝑖𝑗 (𝑥𝑗 ) 𝑦𝑖𝑘 (𝑥𝑘 ) 𝑝𝑖 = 𝑝𝑖𝑗 (𝑥𝑖 ) Component-based approach to modeling 𝑝𝑖𝑘 (𝑥𝑖 ) Proposed Modeling Approach Represent components of power systems using a two-level model which separates their internal dynamics from the dynamics of their interactions Internal dynamics are described using internal dynamic states 𝑥 Interaction dynamics are described using interaction variables 𝑧 Two-level module description 𝑥𝑖 = 𝑓𝑖 𝑥𝑖 , 𝑧𝑖 , 𝑃𝑖𝑘 , 𝑃𝑖𝑗 , 𝑢𝑖 , 𝑑𝑖 𝑧𝑖 = 𝑔𝑖 𝑥𝑖 , 𝑧𝑖 , 𝑃𝑖𝑘 , 𝑃𝑖𝑗 , 𝑢𝑖 , 𝑑𝑖 Interaction variable-based modeling M. Cvetkovic, M. Ilic, “A Two-level Approach to Tuning FACTS for Transient Stabilization”, IEEE PES General Meeting, July 2014. Interaction variable 𝒛 is the accumulated energy inside a module. Proposed Cooperative Controller Accumulated (stored) energy in an uncontrolled system Generator FACTS Redistribute energy of disturbance Cooperative control is expressed in terms of higher (interaction) level dynamics Enabled by using time scale separation between interaction and internal level dynamics Accumulated (stored) energy in a system controlled by power electronics Generator FACTS M. Cvetkovic, M. Ilic, “Ectropy-based Nonlinear Control of FACTS for Transient Stabilization”, IEEE Transactions on Power Systems, Vol. 29, No. 6, November 2014, pp. 3012-3020. SGRS Hierarchical Distributed Simulation of Dynamics Aggregation od dynamics using interaction variables separates the rate of exchange of information and the rate of internal state computations Interactions coming from other modules at time n Interaction variable update at a slower rate n Interaction at n+1 Zoom-out level States at k+1 Internal states update at a faster rate k Zoom-in level Interactions going toward other modules at time n+1 M. Cvetkovic, M. Ilic, “Dynamic Simulation of Power System Transients in Energy State Space”, in preparation. Response of Uncontrolled System Short circuit at bus 3 in duration of 0.35 sec M. Cvetkovic, M. Ilic, “Cooperative Line-flow Power Electronics Control for Transient Stabilization”, IEEE Conference on Decision and Control, December 2014. Controlled System Response 𝑃𝜏3 = 1 𝜏3 𝑃𝜏2 𝑑𝑡 𝜏2 𝑧2 = 0 FACTS energy has reached zero States converge to a different equilibrium 22 M. Cvetkovic, M. Ilic, “Cooperative Line-flow Power Electronics Control for Transient Stabilization”, IEEE Conference on Decision and Control, December 2014. Questions?