* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Outline - 正修科技大學
Power MOSFET wikipedia , lookup
Microwave transmission wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Phase-locked loop wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Nanofluidic circuitry wikipedia , lookup
Waveguide filter wikipedia , lookup
Power dividers and directional couplers wikipedia , lookup
Superheterodyne receiver wikipedia , lookup
Standing wave ratio wikipedia , lookup
Flexible electronics wikipedia , lookup
Equalization (audio) wikipedia , lookup
Zobel network wikipedia , lookup
Regenerative circuit wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Radio transmitter design wikipedia , lookup
Integrated circuit wikipedia , lookup
Distributed element filter wikipedia , lookup
RLC circuit wikipedia , lookup
Chapter 3
Transmission Lines
Contents
1.
2.
3.
4.
Features of Transmission Lines
Low Frequency Characters of Microstrip Line
High Frequency Characters of Microstrip Line
Discontinuities of Microstrip Line
Features of Transmission Lines
Microwave Integrated Circuit (MIC)
The current trend of circuit design is toward miniaturization and integration.
An MIC consists of an assembly that combines different circuit functions
that are connected by transmission lines.
The advantages of MIC compare to traditional circuit using printed circuit
Higher reliability
Planar configuration
Reproducibility
Easy fabrication
Better performance
Lower cost
Higher Integrated
Lighter weight
Smaller size
Two classes of MIC
HMIC
MMIC
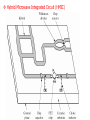
Hybrid Microwave Integrated Circuit (HMIC)
Photograph of one of the 25,344 hybrid integrated T/R modules used in
Raytheon’s Ground Based Radar system. This X-band module contains
phase shifters, amplifiers, switches, couplers, a ferrite circulator, and
associated control and bias circuitry.
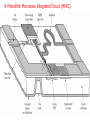
Monolithic Microwave Integrated Circuit (MMIC)
Photograph of a monolithic integrated X-band power amplifier. This
circuit uses eight heterojunction bipolar transistors with power
dividers/combiners at the input and output to produce 5 watts.
Material selection is an important consideration for any type of MIC;
characteristics such as electrical conductivity, dielectric constant, loss
tangent, thermal transfer, mechanical strength, and manufacturing
compatability must be evaluated.
Features of HMICs:
1. Alumina, quartz, and Teflon fiber are commonly used for substrates.
2. During HMICs testing, tuning or trimming for each circuit is allowed
to adjust components values.
Features of MMICs:
1. The substrate of an MMIC must be a semiconductor material to
accommodate the fabrication of active devices. Hence GaAs is the
most common substrate. Besides, Si, sapphire, and InP are also used.
2. All passive and active components are grown or implanted in the
substrate. A single wafer can contain a large number of circuits.
3. Circuit trimming after fabrication will be difficult, even impossible.
Conventional coaxial lines and waveguides are remain useful in :
1. High power transmission (e.g. KW~MW transmitters)
2. High Q component needed (e.g. low loss filter)
3. Some millimetric–wavelength systems (e.g. MW automotive radar)
4. Very low loss transmission systems
5. Precision instrumentation equipment
Planar technology are already tending to overcome problems in areas (2)
and (3), but not (1) or (4).
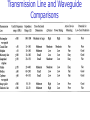
Transmission
Line and
Waveguide
Structures
Transmission Line and Waveguide
Comparisons
Planar
Transmission
Line Structures
Modifications of Planar Transmission
Line Structures
Image Line
Behavior likes a dielectric slab waveguide (thick strip) for use at
operation frequency into hundreds GHz.
Several thousand unloaded Q-factor. But fop Q .
Poor compatibility with active devices, mutual coupling, and radiation
from discontinuities and bends.
Microstrip
The most popular MIC TL with a very simple geometric planar structure.
Advantage: Zero cutoff frequency , light weight, small size, low cost,
easy fabrication and integration, low dispersion , and broadband
operation (frequency range from a few GHZ, or even lower, up to at least
many tens of GHz).
At millimetre-wave range, problems such as loss, higher-order modes,
and fabrication tolerances become exceedingly difficult to meet using
HMICs.
Finline (E-plane circuit)
Advantage:
1) Low loss (typically a factor about three better than microstrip.
2) Simpler fabrication in comparison with inverted and trapped-inverted
microstrip.
3) Operation frequency up to 100GHz.
Disadvantage in biasing problem.
Application in compatibility with solid-state device is fairly good,
especially in the case of beam-lead devices, 10% bandwidth of band
pass filters, quadrature hybrids, waveguide transitions, and balanced
mixer circuits.
Inverted Microstrip (IM)
Advantages in comparison with microstrip :
1) Wider line width for the same Z0, and this both reduces conductor
dissipation and relaxes fabrication tolerances.
2) Structure utilizing air between the strip and ground plane gives higher
Q, wavelength, operation frequency, and avoids interference.
Slotline
Guide mode of architecture makes it particularly suitable for applications
where substrate is ferrite (components such as circulators and isolators).
Disadvantages :
1) Z0 below 60 are difficult to realize.
2) Q factor is significantly lower than other structures considered here.
3) Circuit structures often involve difficult registration problems
( especially with metallization on the opposite side to the slot).
Trapped Inverted Microstrip (TIM)
Advantages is similar to that of IM; moreover, a ‘slot’ or ‘channel’-shaped
ground plane provides inherent suppression of some higher-order modes
Manufacturing difficulties are particularly significant with HMICs.
Coplanar Waveguide (CPW)
Advantages in comparison with microstrip :
1) Easier grounding of surface-mounted ( or BGA mounted) component.
2) Lower fabrication costs.
3) Reduced dispersion and radiation losses.
4) Photolithographically defined structures with relatively low
dependence on substrate thickness.
The major problem is non-unique Z0 because infinite range of ratio
between centre strip width and gap width (In micrpstrip, Z0 is unique
decided by strip width, substrate height, and substrate permittivity).
Coplanar Strip (CPS) and Differential Line
CPS : one of the conductors is ground; Differential line : neither of the
conductors is grounded.
Advantage of differential line:
1) It is suitable for RFICs and high-speed digital ICs (but not for HMIC
due to radiation losses and most passive components are single-ended).
2) This line is popular for use in long bus lines and clock distribution nets
on chip as the signal return path.
The differential line has a virtual ground itself, which means that a real
metallic ground is not necessary.
Stripline
Completely filled microstrip, i.e. a symmetrical structure results in TEM
transmission
Advantages :
1) lower loss.
2) Fairly high Q-factor.
3) Waveguide modes can easily to exited at higher frequencies.
Disadvantages:
1) Insufficient space for the incorporation of semiconductor devices.
2) Mode suppression gives rise to design problem.
3) Not compatible with shunt-mounted devices.
Summary of TL Properties
Z0 and Q-factor are criterion for circuit applications.
Substrate Choice for HMIC
Many factors, mechanical, thermal, electronics, and economic, leading to
the correct choice of substrate deeply influence MIC design.
The kinds of questions include:
1) Cost
2) Thin-film or thick-film technology
3) Frequency range
4) Surface roughness (this will influence conductor losses and metal-film
adhesion)
5) Mechanical strength, flexibility, and thermal conductivity
6) Sufficient surface area
Commonly used substrate materials
Organic PCBs (Printed Circuit Boards)
FR4
1) Low cost, rigid structure, and multi-layer capability.
2) Applications for operation frequency below a few GHz. fop Loss
RT/Duroid
1) Low loss and good for RF applications.
2) Board has a wide selected range for permittivity. e.g. RT/Duroid 5870
with r =2.33, RT/Duroid 5880 with r =2.2, and RT/Duroid 6010 with r
=10.2.
3) Board is soft leading to less precise dimensional control.
Softboard
1) Plastic substrate with good flexibility.
2) This board is suitable for experimental circuits operating below a few
GHz and array antennas operating up to and beyond 20 GHz.
Ceramic Substrate (Alumina)
1) Good for operation frequency up to 40 GHz.
2) Metallic patterns can be implemented on ceramic substrate using thinfilm or thick-film technology.
3) Passive components of extremely small volume can be implemented
because the ceramic substrate can be stacked in many tens of layers or
more, e.g. low temperature co-fired ceramic (LTCC).
4) Good thermal conductivity.
5) Alumina purity below 85% should result in high conductor and
dielectric losses and poor reproducibility.
Quartz
1) Production circuits for millimetric wave applications from tens of GHz
up to perhaps 300 GHz, and suitable for use in finline and image line MIC
structures.
2) Lower permittivity of property allows larger distributed circuit
elements to be incorporated.
Sapphire
The most expensive substrate with following advantages:
1) Transparent feature is useful for accurately registering chip devices.
2) Fairly high permittivity (r =10.1~10.3), reproducible ( all pieces are
essentially identical in dielectric properties), and thermal conductivity
(about 30% higher than the best alumina).
3) Low power loss.
Disadvantages:
1) Relatively high cost.
2) Substrate area is limited (usually little more than 25 mm square).
3) Dielectric anisotropy poses some additional circuit design problems.
Properties of Some Typical Substrate Materials
MIC Manufacturing Technology
Thin-Film Module
Circuit is accomplished by a plate-through technique or an
etch-back technique.
Thick-Film Module
1) Thick-film patterns are printed and fired on the ceramic substrate.
2) Printed circuit technique is used to etch the desired pattern in a plastic
substrate.
Medium-Film Module
Above technologies are suitable for HMIC productions.
Monolithic Technology
This technology is suitable for MMIC productions.
Properties of Various Manufacturing Technology
Multi-Chip Modules (MCM)
MCM provides small, high precision interconnects among multiple ICs to
form a cost-effectively single module or package.
Four dominant types of MCM technologies:
1) MCM-L having a laminated PCB-like structure.
2) MCM-C based on co-fired ceramic structures similar to thick-film
modules.
3) MCM-D using deposited metals and dielectrics in a process very similar
to that used in semiconductor processing.
4) MCM-C/D having deposited layers on the MCM-C base
Advantages of an MCM over a PCB are :
1) Higher interconnect density.
2) Finer geometries enables direct chip connect.
3) Finer interconnect geometries enables chips placed closer together
and it results in shorter interconnect lengths.
Comparison of MCM Technologies
Low Frequency Characters
of Microstrip Line
Microstrip Line
Microstrip line is the most popular type of planar transmission lines,
primarily because it can be fabricated by photolithographic processes and is
easily integrated with other passive and active RF devices.
When line length is an appreciable fraction of a wavelength (say 1/20th
or more), the electric requirements is often to realize a structure that
provides maximum signal, or power, transfer.
Example of a transistor amplifier input network
Microstrip components
Transmission line
Discontinuities
•Step
•Mitered bend
•Bondwire
•Via ground
The most important dimensional parameters are the microstrip width w,
height h (equal to the thickness of substrate), and the relative permittivity of
substrate r.
Useful feature of microstrip :
DC as well as AC signals may be transmitted.
Active devices and diodes may readily be incorporated.
In-circuit characterization of devices is straightforward to implement.
Line wavelength is reduced considerably (typically 1/3) from its free
space value, because of the substrate fields. Hence, distributed
component dimensions are relatively small.
The structure is quite rugged and can withstand moderately high
voltages and power levels.
Although microstrip has not a uniform dielectric filling, energe transmission
is quite closely resembles TEM; it’s usually referred to as ‘quasi-TEM’.
Electromagnetic Analysis Using Quasi-Static
Approach (Quasi-TEM Mode)
The statically derived results are quite accurate where frequency is below a
few GHz.
The static results can still be used in conjunction with frequency-dependent
functions in closed formula when frequency at higher frequency.
Characteristic Impedance Z0
For air-filled microstrip lines,
L
Z0
C
For low-loss microstrip lines,
L
1
1
Z01
cL L 2
C1 cC1
c C1
We can derive
1
Z
c
Z0
01 ; eff
C1
c CC1
eff
Procedure for calculating the distributed capacitance:
Lapace' s equation : t 2Vt0 ( x, y ) 0
0
V
( x, y )
t
0
0
0
BCs for Vt , Et , Dt at y 0 and y h
0
Gauss' s Law
Et tVt0
Q
w
0
0 Q D 0 ds C c f ( , r )
c
t
V0
h
Dt Et
c
w
C1 f ( , r 1)
h
Effective Dielectric Constant
eff
c 2 C
w
( )
g( ,r )
vp
C1
h
For very wide lines, w / h >> 1
eff r
For very narrow lines, w / h << 1
eff
r 1
2
r
w
q 1
h
w
r q 1 / 2
h
We can express eff as
eff 1
eff 1 q ( r 1) q
r 1
1 eff r
where filling factor q represents the ratio of the EM fields inside the
substrate region, and its value is between ½ and 1. Another
approximate formula for q is
q
r ( eff 1)
eff ( r 1)
(provided by K.C. Gupta, et. al.)
r 1
Planar Waveguide Model
(Parallel-Plate Model)
Z0
h0
weff eff
r
()
where 0 0 0 120
eff
Conductor
Loss ac
In most microstrip designs with high r, conductor losses in the strip and
ground plane dominate over dielectric and radiation losses.
It’s a factors related to the metallic material composing the ground
plane and walls, among which are conductivity, skin effect, and surface
roughness.
Relationships:
h
ac
, roughness of the substrate surface.
w
ac opposite to conductivi ty ( In idealized line, )
The strip thickness should be greater th an 3 ~ 5 times the skin depth to minimize ac .
Dielectric Loss ad
To minimize dielectric losses, high-quality low-loss dielectric substrate
like alumina, quartz, and sapphire are typically used in HMICs.
In MMICs, Si or GaAs substrates result in much larger dielectric losses
(approximately 0.04 dB/mm).
Radiation
Loss ar
Radiation loss is major problem for open microstrip lines with low .
Lower (5) is used when cost reduction is a priority, but it lead to
radiation loss increased.
The use of top cover and side walls can reduce radiation losses. Higher
substrate can also reduce the radiation losses, and has a benefit in that
the package size decreases by approximately the square root of . This
benefit is an advantage at low frequency, but may be a problem at higher
frequencies due to tolerances.
Formulations of Attenuation Constant
R
2R 1
R
ac
s
s (Np/m )
2Z0
w 2 Z 0 wZ0
a
GZ0 1
L 1 tan c
1
ad
(C )
(
) LC LC tan c
2
2
C 2
2
1
1
1
tan c 0 0 eff tan c k0 eff tan c (Np/m )
2
2
2
where k0 0 0 / c (free - space wavenumbe r)
However, the dielectric loss should occur in the substrate region only,
not the whole region. Therefore, ad should be modified as
r ( eff 1) 1
1
a d q k0 eff tan c
k0 eff tan c
2
eff ( r 1) 2
k0 r ( eff 1) tan c
(m -1 )
2 eff ( r 1)
How to evaluate attenuation constant
a
Method 1 : in Chapter 2.14 ; a is calculated from RLCG values of material.
Method 2: Perturbation method
a
Pl ( z 0)
where Pl is power loss per unit length of line,
2 P0
P0is the power on line at z=0 plane.
Method 3:a is calculated from material parameters.
a ac ad a r where ac is attenuation due to conductor loss
ad is attenuation due to dielectric loss
Rs dZ 0
ac
ar is attenuation due to radiation loss
2 Z dl
0
k 2 tan
ad
; unit : Np/m (for TE or TM waves)
2
k tan
ad
; unit : Np/m (for TEM waves)
2
Combined Loss Effect : linearly combined quality factors (Q)
1
1
1
1
Q Qc Qd Qr
Recommendations
1) Use a specific dimension ratio to achieve the desired characteristic
impedance. Following that, the strip width should be minimized to
decrease the overall dimension, as well as to suppress higher-order
modes. However, a smaller strip width leads to higher losses.
2) Power-handling capability in microstrip line is relatively low. To
increase peak power, the thickness of the substrate should be
maximized, and the edges of strip should be rounded ( EM fields
concentrate at the sharp edges of the strip).
3) The positive effects of decreasing substrate thickness are :
a) Compact circuit
b) Ease of integration
c) Less tendency to launch higher-order modes or radiation
d) The via holes drilled through dielectric substrate contributing
smaller parasitic inductances
However, thin substrate while maintaining a constant Z0 must narrow
the conductor width w, and it consequently lead to higher conductor
losses, lower Q-factor and the problem of fabrication tolerances.
4) Using higher substrate can decrease microstrip circuit dimensions,
but increase losses due to higher loss tangent. Besides, narrowing
conductor line have higher ohmic losses. Therefore, it is a conflict
between the requirements of small dimensions and low loss. For
many applications, lower dielectric constant is preferred since losses
are reduced, conductor geometries are larger ( more producible), and
the cutoff frequency of the circuit increases.
5) For microwave device applications, microstrip generally offers the
smallest sizes and the easiest fabrication, but not offer the highest
electrical performance.
Design a
microstrip line by
the method of
“Approximate
Graphically-Based
Synthesis”
Example1: Design a 50 microstrip line on a FR4 substrate( r =4.5).
Solution
Assume eff = r =4.5
From Zo1 curve w/h=1.5
From q-curve
q=0.66
eff = 1+q (r +1)=1+0.66(4.5-1)=3.31
2nd iteration
Z 01 Z 0 eff 50 3.31 91
From Zo1 curve w/h=1.7
From q-curve
q=0.68
eff = 1+q (r +1)=1+0.68(4.5-1)=3.38
3rd iteration
Stable result
w/h=1.88; eff =3.39
Formulas for Quasi-TEM Design Calculations
Analysis procedure: Give w / h to find eff and Z0.
(provided by I.J. Bahl, et. al.)
r 1
r 1
eff
2
2 1 12 (h / w)
8h w
60
ln(
),
w 4h
eff
Z0
120
,
eff ( w h) 1.393 0.667 ln (1.444 w / h)
Synthesis procedure: Give Z0 to find w / h.
A
8e
w
1
h
w
1
h
w
2
2A
w e 2
h
h 2
r 1
0.61 w
ln ( B 1) 0.39
2
B 1 ln (2 B 1)
,
2 r
r h
Z0 r 1 r 1
0.11
377
where A
(0.23
), B
60
2
r 1
r
2Z0 r
Example2: Calculate the width and length of a microstrip line for a 50
Characteristic impedance and a 90° phase shift at 2.5 GHz. The
substrate thickness is h=0.127 cm, with eff =2.20.
Solution
Guess w/h>2
377
B
7.985
2Z0 r
w 2
r 1
0.61
B 1 ln ( 2 B 1)
ln ( B 1) 0.39
3.081
h
2 r
r
Then w=3.081h=0.391 (cm)
eff
r 1
2
r 1
2 1 12 (h / w)
1.87
The line length, l, for a 90° phase shift is found as
90 l k l
k 2f
eff
0
90 ( / 180 )
l
2.19 (cm)
eff k0
0
c
52.35 (m -1 )
Matched
with
guess
Microstrip on an Dielectrically Anisotropic Substrate
x
0
0
0
y 0
0 z
0
0
0 0 9.4
Sapphire 0 || 0 0 11.6 0
9.4
0
0 0 0
C yC y
; where
req i f
C f Cy
0
C f Ci i 0 ( w / h ) denotes fringing capacitnce
Cy y 0 ( w / h ) denotes parallel - plate capacitnce
Empirical formula
1.21
;
2
1 0.39[log( 10w / h)]
0.5% accuracy throughout the range
eff 12
0.1 w / h 10
and
10 Z 0 100
Curve : i =10.6 ;
Curve : used req formula
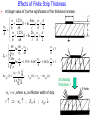
Effects of Finite Strip Thickness
At larger value of t/w the significance of the thickness increase.
4πw w
w 1.25t
(1
ln
);
we h
h
t
h 2
h w 1.25t (1 ln 2h ); w
h
t h 2
h
8h we
w
60
ln(
),
1
we 4h
h
eff
Z0
120 ln( we 1.393 0.667 we 1.444), w 1
h
h
h
eff
( r 1) t
h ; (t ) (t )
eff (t )
eff
eff
eff
w
4.6
h
we w
,where we is effective width of strip
t we ; Z0 ; eff
Increasing
thickness t
E-fields
Effects of Metallic Enclosure (Housing)
The purpose of metallic enclosure provide hermetic sealing, mechanical
strength, EM shielding, connector mounting, and module handling.
The conducting top and side walls lower both eff and Z0, which is due to
increase proportion of electric flux in air.
r 1
r 1
h ' 0.415
eff
(
R ) tanh[ 0.18 0.237 '
]
2
2
2
h (h )
h
h 0.5
w 2 w
[
1
12
(
)]
0
.
04
(
1
) ,
1
w
h
h
R
h
w
[1 12( )]0.5 ,
1
w
h
w
Z
(
unshielded
)
Z
,
1.3
0 s1
0
h
Z 0 (shielded )
w
Z 0 ( unshielded ) Z 0 s 2 ,
1.3
h
Z 0 s1 270[1 tanh( 0.28 1.2 h ' h )]
Z0s 2
0.48[( we h ) 1]0.5
Z 0 s1 (1 tanh{ 1
})
'
2
[1 (h h )]
Effects of Propagation Delay
One of the most significant properties of microstrip for applications in high
speed digital or time-domain applications ( e.g. computer logic, digit
communication, sampler for oscilloscope, counter) to carry signal pulses is
propagation delay.
Crosstalk between adjacent circuits is a serious problem in pulse systems.
d
eff
c
; s/m
d
1
; vp
vp
1
LC
For example, a 50 microstrip line on high-purity alumina: eff =6.7
d
6.7
8.6 ns/m 8.6 ps/mm
8
3 10
High-speed gates typically have
around 50 ps delay per gate, it means
that 5-10 mm of microstrip is needed
to realize such a gate. For instance,
such length of line is not feasible to
implement in chips.
L or C d length of line
Recommendations to The Static-TEM Approaches
The Static-TEM formulas will exhibit significant errors once operation
frequency beyond a few GHz.
Always start with a slightly lower impedance than the actually desired, i.e.
larger w/h, if trimming (etch or laser-trim) is contemplated.
The physical lengths of line should slightly longer than required for
adjusting operation frequency. In general, 1% reduction in length can be
expected approximately a 1% increase in frequency.
The length of a top-cover shield might be adjusted to trim the performance
of MICs.
High Frequency Characters
of Microstrip Line
Dispersion in Microstrip (Frequency Dependence)
r
Microstrip Line
eff 0
High loss
Low dispersion
air
0 0 eff
Planar Waveguide Model
Microstrip Line
Medium loss
High dispersion
substrate
Low loss
Low dispersion
Good for Applications
As frequency goes higher, EM fields tend to distribute in the substrate
region in a higher ratio.
Frequency-Dependent Effective Dielectric Constant
(f ) for Microstrip Line
eff
The reason of dispersion generated :
1) Higher TE and TM modes
(hybrid mode) generated
2) Surface wave couples with
dominate mode
eff ( f , h, r )
Getsinger Formula :
2
eff ( f )
( )
0 0
r eff ( f 0)
r
2
1
eff ( f ) always increase with frequency
eff ( f 0) eff ;
eff ( f ) r ;
1 G ( f / fp)
where f p Z 0 /( 2 0h ),
G is empirical formula and sensitive to Z 0
For alumina ( eff 9.9) with h 0.635mm
G 0.6 0.009 Z 0 ;
For sapphire ( eff 10.7 ~ 11.6) with h 0.5mm
G [( Z 0 5) / 60]2 0.004 Z 0 ;
wel l with range 10 Z 0 100, 2 f 18GHz
For alumina ( eff 10.15) with h 0.65mm
Z0 3 2
G(
) 0.001Z 0 ; well with range 30 Z 0 70, 2 f 18GH
60
Example3: Design a 50- microstrip line on a 0.635 mm thick ceramic
substrate (r=9.9). Calculate the wavelength of the line at 1 and 10 GHz.
Assume that G = 0.6 + 0.009 Z0 in Getsinger’s expression.
Solution
50 9.9 1 9.9 1
0.11
A
(0.23
) 2.142
60
2
9.9 1
9.9
w
8e2.142
0.966
2
2
.
142
h e
2
w 0.966 0.635 0.613 (mm)
9.9 1
9.9 1
eff ( f 1GHz)
6.664
2
2 1 12(0.635 / 0.613)
3 108
at 1 GHz
10
fp
9
0.1162 (m) 116.2 (mm)
6.664
50
2 4 10 7 0.635 10 3
31.33 109 (Hz) 31.33 (GHz)
G 0.6 0.009 50 1.05
eff ( f 10GHz) 9.9
at 10 GHz
9.9 6.664
1 1.05 (10 / 31.33)
3 108
10
10
6.977
2
6.977
0.01136 (m) 11.36 (mm)
Other accurate formulas of
eff (f )
Edwards and Owens’ expression : applicable for alumina and sapphire
substrate under the range 10 r 12 (alumina type) and f18 GHz.
eff r
r eff
1 (h Z0 )
1.33
(0.43 f 0.009 f )
2
3
; where h is in mm and f is in GHz
Yamashita expression : suitable for millimetre-wave design (up to 100GHz)
but not accuracy for frequency below 18 GHZ.
eff ( f ) (
r eff
eff )2 ,
1 4 F 1.5
4hf r 1
w 2
F
[0.5 {1 2 log( 1 )} ]
c
h
Advantage of these formulas are calculated-based design and
inexpensively integrated into CAD tools. However, these approximate
approaches based on some limited applications are their drawback.
Frequency-Dependent of Microstrip Characteristic
Impedance (Z0)
The problem of characteristic impedance as a function of frequency is
difficult to settle. Because there are several definitions of Z0 used different
assumptions to derive results.
Planar waveguide model
Z0 ( f )
h
weff ( f ) eff ( f )
weff ( f ) w
fp
weff w
1 ( f f p )2
c
V
I
P
*
II
VV *
P
Z 0 ,a
Z 0,b
Z 0 ,c
2 weff eff
weff
h
Z 0 eff
; 0 0
f weff ; Z0 ( f )
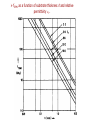
For a 50 line the increase is about 10% over 0-16GHz range
Dispersion of lossy gold
microstrip on a 635m thick
alumina substrate (r =9.8,
w= 635m, Z0 =50)
Dispersion of lossy copper
microstrip on a 650m thick
high resistivity silicon
substrate (r =11.9,
w= 70m, Z0 =83)
Variation of effective permittivity and characteristic impedance for a
lossy gold microstrip on a 635m thick alumina substrate (r =9.8)
Operation frequency Limitation
Two possible spurious effects restrict the desirable operating frequency:
1) The lowest-mode TM mode: the most significant modal limitation in
microstrip are associated with strong coupling between the dominant
quasi-TEM mode and the lowest-order TM mode.
2) The lowest-order transverse microstrip resonance.
TM mode: it is identified when the associated two phase velocities are close.
Effective
1
c tan ( r )
air
mode
f
TEM 1
2( r 1)h
The maximum restriction on
usable substrate thickness:
hM
0.3450
fTEM1
substrate
TM0
Quasi-TEM
r 1
hM fTEM1
fTEM1 can be regarded as the upper limitation of operating frequency.
fTEM1 as a function of substrate thickness h and relative
permittivity r .
Lowest-Order Transverse Microstrip Resonance
Transverse microstrip resonance: For a sufficiently wide microstrip the
resonant mode can also couple strongly to quasi TEM mode.
To suppress transverse resonance, slot can introduce into metal strip but
sometimes it might excite resonance. A practice method is a change in
circuit configuration to avoid wide microstip lines close adjacent.
At the cutoff frequency of transverse resonant mode, line has a length
equivalent to w+2d, where d accounts for the microstrip side-fringing
capacitance: d=2h.
The cutoff frequency:
fCT
c
r (2w 0.8h)
Parameters governing the choice of substrate for any
microstrip application.
Power Losses and Parasitic Coupling
Four separate mechanisms can be identified for power losses and parasitic
coupling:
1) conductor losses
2) dissipation in the dielectric of substrate
3) radiation loss
4) surface-wave propagation
Dissipative effects
Parasitic phenomena
The dissipative losses may be interpreted in terms of Q factor or can be
lumped together as the attenuation coefficent a.
Conductor Loss
f
a c 0.072
g (dB/microstrip wavelength)
wZ 0
g 0
eff
f -1/2 , h-1
; where f is in GHz and Z 0 is in .
In practice the loss is approximately 60 % increased when surface
roughness is taken into account.
Dielectric Loss
r ( eff 1) tan
a d 27.3
eff ( r 1)
(dB/microstrip wavelength)
Independent f , h
In general conductor loss greatly exceed dielectric loss for most
microstrip lines on alumina or sapphire substrates, but opposite condition
to have larger dielectric loss for Si or GaAs substrates.
a ac ad
Q
Qg
;
2a ag
(Np/m)
2 g
f a Q
However Q factor will be limited by parasitic effects at high frequencies.
Radiation
f 2, h 2
Microstrip is an asymmetric TL structure and is often used in unshielded
or poorly shielded circuits where any radiations is either free to
propagate away or to induce currents in the shielding. Further power loss
is the net result.
Discontinuities of microstrip form essential features of a MIC and are the
major sources of radiations unavoidably.
Various techniques may be adopted to reduce radiation:
1) Metallic shielding or ‘screening’.
2)A lossy (absorbent) material near any radiation discontinuity.
3) Possibly shape the discontinuity in some way to reduce the radiation
efficiency.
Surface-Wave Propagation
f 3~4 , h3~4
Surface wave trapped just beneath the surface of substrate dielectric, will
be propagated away from microstrip discontinuities in the form of a
range of TE or TM modes.
This effect can be reduced by above methods 1 and 2 , or by cutting
slots into the substrate surface just in front of an open-circuit.
Power losses versus
frequency for open-end
discontinuity (r =10.2,
w= 24 mil, h =25 mil)
Parasitic Coupling
If shielding cannot be adopted due to space limitation as to use the
absorbent material, the method will reduces the Q-factor .
High degree of isolation can suppress the parasitic coupling.
Various methods for increasing isolation:
1) Use relatively high permittivity substrate.
2) Use fairly thin substrate.
3) Employ high impedance stubs, wherever this is feasible.
Conclusion :
Attenuation is mainly due to conductor and dielectric losses.
Radiation and surface-wave losses are negligible.
This face can be observed from the relative degree that these losses
dependent to frequency.
Recommendations for Higher frequency Considerations
Select the substrate such that the TM mode effect is avoided. fTEM1 , hM
Check that the first-order transverse resonance cannot be exited at the
highest frequency. If a resonance is occur, above mentioned solutions can
be adopted to suppress. fCT
Calculate the total losses and Q-factor to check if they satisfy the design
requirement. A reappraisal of design philosophy may be necessary when
Q-factor is too low.
Evaluate the frequency-dependent effective microstrip parameters to
account for high-frequency effects. e.g. eff (f ), Z0(f )
Discontinuities of Microstrip Line
The Main Discontinuities
All practical distributed circuits must inherently contain discontinuities.
Such discontinuities give rise to small capacitances and inductances
( often < 0.1pF and < 0.1nH) and these reactances become
significant at high frequencies.
Several form of discontinuities :
1. Open-end circuit (Stub)
2. Series coupling gaps
3. Short-circuit through to the ground plane (Via)
4. Right-angled corner (Bend)
5. Step width change
6. Transverse slit
7. T-junction
8. Cross-junction
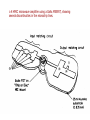
A HMIC microwave amplifier using a GaAs MESFET, showing
several discontinuities in the microstrip lines.
Open-End
Three phenomena associated with the open-end :
1. Fringing fields. Cf
2. Surface waves.
3. Radiation.
Terms 2 and 3 equivalent to a shunt conductance (G), but minimization
can be carried out to suppress the effects.
Curve-fitting formula (by Silvester and Benedek):
Cf
5
i 1
h
exp[ 2.2036 k (log
Coefficients for k
)i 1 ] ; pF/m
Equivalent End-Effect Length
The microstrip line is longer than it actually is to account for the endeffect.
cZ 0C f
leo
;
eff
accuracy over the range 2 f 20 GHz
and alumuna substrate less than 1 mm thick.
More general formula :
(by Hammerstad and Bekkadal)
w 0.262
eff 0.3
leo 0.412h(
)( h
)
eff 0.258 w 0.813
h
Over a wide range of materials and w/h,
the expression gives error of 5%.
Where such error is accepted.
Upper limit to end-effect length (by Cohn):
(
leo
2
) max ln 2
h
Cf : equivalent and fringing
capacitance
Leo : equivalent extra TL of
length
Normalized end-effect length (Leo /h ) as a function of
shape ratio w /h.
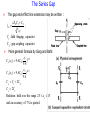
The Series Gap
The gap end-effect line extension may be written :
leo
cZ 0C1 C2
eff
;
C1 : field fringing capacitor
C2 : gap coupling capacitor
More general formula by Garg and Bahl:
Co ( r ) 9.6C0 (
Ce ( r ) 9.6Ce (
r
9.6
r
9.6
)0.8
)0.9
Co C1 2C2
Ce 2C1
Relations hold over the range 2.5 r 15
and an accuracy of 7% is quoted.
Via-Ground
The via hole provides a fairly good short-circuit to ground at lower
frequency range, but the parasitic effects increase at high frequencies.
Optimum via-hole dimension for minimum reactance ( by Owens):
weff
weff 2
ln(
)(
) ;
d e
d e
d e 0.03 0.44d (d : actual hole diameter)
weff
h0
Z 0 eff
(effective microstrip width)
For a 50 line on alumina substrate
(r =10.1, h=0.635mm), the hole diameter
needs 0.26mm for a good broadband
short-circuit. To accurately and repeatably
locate these holes or ‘shunt posts’,
Computer-controlled laser drilling can provide
Precision realization.
Lvia
C fringing
Grad surf
Right-Angle Bend or Corner
The bend usually pass through an angle of 90° and the line does not
change width.
The capacitance arises through additional charge accumulation at the
corners particularly around the outer part of bend where electric fields
concentrate.
The inductance arise because of current flow interruption.
Reactance formula ( by Gupta):
C (14 r 12.5) w h (1.83 r 2.25)
pF/m; For w 1
h
w
wh
C
w
(9.5 r 1.25) 5.2 r 7 pF/m; For w 1
h
w
h
L
w
100[4
4.21] nH/m
h
h
Accuracy is within 5% over the range :
2.5 r 15 and 0.1 w 5.0
h
Example4: Calculate the parasitic effects for a bend on an w=0.75mm
and h=0.5mm alumina substrate (r=9.9).
Solution
For w 1.5 1
h
C 0.135pF and L 0.031nH
At 10 GHz
L 2 ; 1/C 120
The 2/120 reactances in
series/parallel connection with 50 line
will have a pronounced influence
on circuit response.
0.031nH 0.031nH
0.135pF
Mitred or Matched Bend
A mitred bend can greatly reduce the effects of reactance and hence
improving circuit performance.
An equivalent line-length lc occurs and increase with enhanced mitred.
The champing function should be restricted to around:
1
b
0.6
2w
b 0.57w
A bend acts like a reflector.
Magnitude of the current densities on
(a) a right-angled bend, and (b) an optimally mitred bend.
The Symmetrical Step
Like the bend, the shunt capacitance is the dominant factor.
Curve-fitting formulas:
Lm 2
Lm1
; L L1 L2
; L2 L
L1 L
Lm1 Lm 2
Lm1 Lm 2
Lm1
Z o1 eff 1
c
; Lm 2
For r 10 ; 1.5 w2
Z o 2 eff 2
w1
c
All inductance s are in nH/m
3.5 :
w2
C
12.6 log r 3.17 pF/m
(10.1 log r 2.33)
w1
w1w2
For r 10 ; 3.5 w2
w1
3.5 :
w
C
130 log( 2 ) 44 pF/m
w1
w1w2
The Asymmetrical Step
The values of reactances are about half of the values obtained for the
symmetrical step.
The Narrow Transverse Slit
A narrow slit yields a series inductance effect, and it may be used to
compensate for excess capacitance at discontinuities or to fine-tune
lengths of microstrip such as stubs.
ΔL 0 a ' 2
( )
h
2 A
Z 0, w
a'
where
1 '
A
Z 0, w a
A narrow slit width causes parasitic capacitance to parallel connection
with L. While wide slit forms the asymmetrical steps. Therefore b < h.
T-Junction
The junction necessarily occurs in a wide variety of microstrip circuits
such as matching elements, stub filters, branch-line couplers, and
antenna element feeds.
Garg et. al. and Hammerstad et. al. have provided formulas for
extracting the elements of equivalent circuit. However, some limitations
to the accuracy of formulas should be noticed.
Parameter trends for the T-junction.
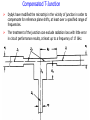
Compensated T-Junction
Dydyk have modified the microstrip in the vicinity of junction in order to
compensate for reference plane shifts, at least over a specified range of
frequencies.
The treatment of the junction can exclude radiation loss with little error
in circuit performance results, at least up to a frequency of 17 GHz.
Cross-Junction
A cross-junction may be symmetrical or asymmetrical, where the lines
forming the cross do not all have the same widths.
Theoretical and experimental agreement is not good, especially for some
inductance parameter.
The coupling effects that occur with cross-junctions illustrates the origin
of cross-talk in complicated interconnection networks.
One kind of applications is that used two stubs placed on each side of
microstrip to instead of single one. The method can prevent wider stub
from sustaining transverse resonance modes at higher operating
frequency.
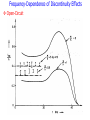
Frequency-Dependence of Discontinuity Effects
Open-Circuit
Edward
Figure
7.27
Edward
Figure
7.25
7.26
Open-Circuit
Open-Circuit
Series Gap
Cross-Junction
Bend