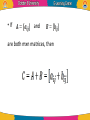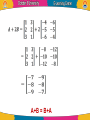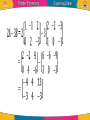Download matrix - O6U E-learning Forum

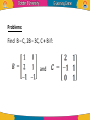
Linear Algebra
by
Dr. Shorouk Ossama
References
“Elementary Linear Equation”,
tenth Edition, Applications Version,
Howard Antion, Chris Rorres.
3.1 Matrix definition:
• We used rectangular arrays of numbers, called
matrices, to abbreviate systems of linear
equations. However,
• Rectangular arrays of numbers occur in other
contexts as well. For example, the following
rectangular array with three rows and seven
columns might describe the number of hours that
a student spent studying three subjects during a
certain week:
A matrix is a rectangular array of numbers. The numbers in the
array are called the entries or element in the matrix. Capital
letters are usually used to denote matrices.
• The matrix with only one column,
𝑏1
B= ⋮ ,
𝑏𝑛
is called a column vector or a column matrix,
• The matrix with only one row ,
a = [ a1 a2 ……. an]
is called a row vector or a row matrix.
• The size of a matrix is described in terms of
the number of rows (horizontal lines) and
columns (vertical lines) it contains.
𝟏 𝟐
• For example, 𝟑 𝟎 the matrix has three
−𝟏 𝟒
rows and two columns, so its size is 3 by 2
(written 3x2).
• A general m×n matrix, one with m rows and
n columns, can be represented by the
notation.
• Where: aij is the element in the ith row and
jth column of A; or A = 𝑎𝑖𝑗 .
• Example:
2 −3
For the matrix, A =
, we have:
7 0
A11 = 2,
A12 = -3,
A21 = 7 and
A22 = 0.
Some Examples of Matrices
• Identity matrix:
A diagonal matrix with all diagonal elements
equal to 1 is called an identity matrix ( I ).
AI = A , IA = A
• Zero matrix:
A matrix whose all entries are zero is called a
zero matrix
A0 = 0
, 0A = 0
• Square Matrix:
If the number of rows of a matrix is equal to
the number of columns of a matrix , that is, ,
then is called a square matrix.
• Upper Triangular Matrix:
A matrix for which for all is called an upper
triangular matrix. That is, all the elements
below the diagonal entries are zero.
• Lower Triangular Matrix:
A matrix for which for all is called a lower
triangular matrix. That is, all the elements
above the diagonal entries are zero.
• Diagonal matrix:
A
square
matrix
with
all
non-diagonal
elements equal to zero is called a diagonal
matrix, that is, only the diagonal entries of the
square matrix can be non-zero,
• Power of Matrices:
If A is a square matrix of order nxn, then we
write AA as A2, AA2 as A3 and so on. If A is
diagonal, as in: Aⁿ = AA∙ ∙ ∙A
• Example:
𝟏 𝟐
If A =
Then
𝟏 𝟑
A3
1 2
=
1 3
1 2
1 3
1 2
11 30
=
1 3
15 41
Operation on Matrices
• it is desirable to develop an “arithmetic of
matrices” in which matrices can be:
1. added,
2. subtracted, and
3. multiplied in a useful way.
Equality
•Two matrices are defined to be equal if they
have the same size and their corresponding
entries are equal.
•The equality of two matrices A = 𝑎𝑖𝑗 and B =
𝑏𝑖𝑗 of the same size can be expressed either
by writing 𝐴 𝑖𝑗 = 𝐵 𝑖𝑗
• Example: Consider the matrices
𝟐 𝟏
𝟐 𝟏
A=
,𝑩 =
𝒂𝒏𝒅
𝟑 𝒙
𝟑 𝟓
𝟐 𝟏 𝟎
𝑪=
Find value of x
𝟑 𝟒 𝒙
If A = B, then x = 5, but there is no value of x
for which since A and C have different sizes.
• Example
Solve the equation A=B when
Since and must have the same elements, if
follows that
Multiplication By a Constant
• If A is any matrix and k is any scalar, then the
product kA is the matrix obtained by
multiplying each entry of the matrix A by k.
The matrix kA is said to be a scalar multiple of
A.
• If A = [aij], then (kA)ij = k (A)ij = k aij
• Example:
𝟐 𝟑 𝟒
For The Matrices A =
,𝑩=
𝟏 𝟑 𝟏
𝟎 𝟐 𝟕
𝟗 −𝟔 𝟑
and C =
−𝟏 𝟑 −𝟓
𝟑 𝟎 𝟏𝟐
4 6 8
We have: 2A =
, (−1)𝐵 =
2 6 2
0 −2 −7
and
1 −3 5
1
3 −2 1
C=
3
1 0 4
• If :
And k= 10, then
Equally, we can 'factorize' a matrix. Thus
Zero Matrix
• Any matrix in which every element is zero is
called a zero or null matrix. If A is a zero
matrix, we can simply write A= 0
A + 0 = 0 + A = A
A–A= 0
0–A=-A
 A 0 = 0; 0 A = 0
Matrix Sums and Differences
• If A and B are matrices of the same size, then
the sum A + B is the matrix obtained by
adding the entries of B to the corresponding
entries of A, and the difference A – B is the
matrix obtained by subtracting the entries of
B from the corresponding entries of A.
• If
and
are both mxn matrices, then
• Matrices of different sizes cannot be added
or subtracted.
•In matrix notation, if A = [aij], then B = [bij]
have the same size, then:
• (A+B)ij = (A)ij + (B)ij = aij + bij and
• (A-B)ij = (A)ij - (B)ij = aij - bij
• Example: Consider the matrices
𝟐
𝟏 𝟎 𝟑
−𝟒
•A = −𝟏 𝟎 𝟐 𝟒 , B = 𝟐
𝟒 −𝟐 𝟕 𝟎
𝟑
𝟏 𝟏
C=
Then
𝟐 𝟐
−2 4 5 4
6
A+B = 1 2 2 3 A-B = −3
7 0 3 5
1
𝟑 𝟓 𝟏
𝟐 𝟎 −𝟏 ,
𝟐 −𝟒 𝟓
−2 −5 2
−2 2 5
−4 11 −5
•The expressions A+C, B+C and B-C are undefined.
• Example
If
Then find A+B, B+A and A+2B.
We have (by Rule 2).
Also
A+B = B+A
• The difference of two matrices is written as
which is interpreted as A - B, A + (-1) B,
• Example:
Find A - B, 2A - 3B if:
and
The rules of arithmetic as applied to the
elements of matrices lead to the following
results for matrices for which addition can be
defined:
Problems:
Find B – C, 2B – 3C, C + B if:
and
Thanks