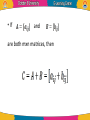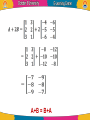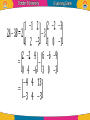* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download matrix - O6U E-learning Forum
Bra–ket notation wikipedia , lookup
Tensor operator wikipedia , lookup
Capelli's identity wikipedia , lookup
Cartesian tensor wikipedia , lookup
Quadratic form wikipedia , lookup
Linear algebra wikipedia , lookup
System of linear equations wikipedia , lookup
Rotation matrix wikipedia , lookup
Eigenvalues and eigenvectors wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Jordan normal form wikipedia , lookup
Determinant wikipedia , lookup
Four-vector wikipedia , lookup
Singular-value decomposition wikipedia , lookup
Matrix (mathematics) wikipedia , lookup
Non-negative matrix factorization wikipedia , lookup
Perron–Frobenius theorem wikipedia , lookup
Matrix calculus wikipedia , lookup
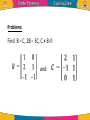
Linear Algebra by Dr. Shorouk Ossama References “Elementary Linear Equation”, tenth Edition, Applications Version, Howard Antion, Chris Rorres. 3.1 Matrix definition: • We used rectangular arrays of numbers, called matrices, to abbreviate systems of linear equations. However, • Rectangular arrays of numbers occur in other contexts as well. For example, the following rectangular array with three rows and seven columns might describe the number of hours that a student spent studying three subjects during a certain week: A matrix is a rectangular array of numbers. The numbers in the array are called the entries or element in the matrix. Capital letters are usually used to denote matrices. • The matrix with only one column, 𝑏1 B= ⋮ , 𝑏𝑛 is called a column vector or a column matrix, • The matrix with only one row , a = [ a1 a2 ……. an] is called a row vector or a row matrix. • The size of a matrix is described in terms of the number of rows (horizontal lines) and columns (vertical lines) it contains. 𝟏 𝟐 • For example, 𝟑 𝟎 the matrix has three −𝟏 𝟒 rows and two columns, so its size is 3 by 2 (written 3x2). • A general m×n matrix, one with m rows and n columns, can be represented by the notation. • Where: aij is the element in the ith row and jth column of A; or A = 𝑎𝑖𝑗 . • Example: 2 −3 For the matrix, A = , we have: 7 0 A11 = 2, A12 = -3, A21 = 7 and A22 = 0. Some Examples of Matrices • Identity matrix: A diagonal matrix with all diagonal elements equal to 1 is called an identity matrix ( I ). AI = A , IA = A • Zero matrix: A matrix whose all entries are zero is called a zero matrix A0 = 0 , 0A = 0 • Square Matrix: If the number of rows of a matrix is equal to the number of columns of a matrix , that is, , then is called a square matrix. • Upper Triangular Matrix: A matrix for which for all is called an upper triangular matrix. That is, all the elements below the diagonal entries are zero. • Lower Triangular Matrix: A matrix for which for all is called a lower triangular matrix. That is, all the elements above the diagonal entries are zero. • Diagonal matrix: A square matrix with all non-diagonal elements equal to zero is called a diagonal matrix, that is, only the diagonal entries of the square matrix can be non-zero, • Power of Matrices: If A is a square matrix of order nxn, then we write AA as A2, AA2 as A3 and so on. If A is diagonal, as in: Aⁿ = AA∙ ∙ ∙A • Example: 𝟏 𝟐 If A = Then 𝟏 𝟑 A3 1 2 = 1 3 1 2 1 3 1 2 11 30 = 1 3 15 41 Operation on Matrices • it is desirable to develop an “arithmetic of matrices” in which matrices can be: 1. added, 2. subtracted, and 3. multiplied in a useful way. Equality •Two matrices are defined to be equal if they have the same size and their corresponding entries are equal. •The equality of two matrices A = 𝑎𝑖𝑗 and B = 𝑏𝑖𝑗 of the same size can be expressed either by writing 𝐴 𝑖𝑗 = 𝐵 𝑖𝑗 • Example: Consider the matrices 𝟐 𝟏 𝟐 𝟏 A= ,𝑩 = 𝒂𝒏𝒅 𝟑 𝒙 𝟑 𝟓 𝟐 𝟏 𝟎 𝑪= Find value of x 𝟑 𝟒 𝒙 If A = B, then x = 5, but there is no value of x for which since A and C have different sizes. • Example Solve the equation A=B when Since and must have the same elements, if follows that Multiplication By a Constant • If A is any matrix and k is any scalar, then the product kA is the matrix obtained by multiplying each entry of the matrix A by k. The matrix kA is said to be a scalar multiple of A. • If A = [aij], then (kA)ij = k (A)ij = k aij • Example: 𝟐 𝟑 𝟒 For The Matrices A = ,𝑩= 𝟏 𝟑 𝟏 𝟎 𝟐 𝟕 𝟗 −𝟔 𝟑 and C = −𝟏 𝟑 −𝟓 𝟑 𝟎 𝟏𝟐 4 6 8 We have: 2A = , (−1)𝐵 = 2 6 2 0 −2 −7 and 1 −3 5 1 3 −2 1 C= 3 1 0 4 • If : And k= 10, then Equally, we can 'factorize' a matrix. Thus Zero Matrix • Any matrix in which every element is zero is called a zero or null matrix. If A is a zero matrix, we can simply write A= 0 A + 0 = 0 + A = A A–A= 0 0–A=-A A 0 = 0; 0 A = 0 Matrix Sums and Differences • If A and B are matrices of the same size, then the sum A + B is the matrix obtained by adding the entries of B to the corresponding entries of A, and the difference A – B is the matrix obtained by subtracting the entries of B from the corresponding entries of A. • If and are both mxn matrices, then • Matrices of different sizes cannot be added or subtracted. •In matrix notation, if A = [aij], then B = [bij] have the same size, then: • (A+B)ij = (A)ij + (B)ij = aij + bij and • (A-B)ij = (A)ij - (B)ij = aij - bij • Example: Consider the matrices 𝟐 𝟏 𝟎 𝟑 −𝟒 •A = −𝟏 𝟎 𝟐 𝟒 , B = 𝟐 𝟒 −𝟐 𝟕 𝟎 𝟑 𝟏 𝟏 C= Then 𝟐 𝟐 −2 4 5 4 6 A+B = 1 2 2 3 A-B = −3 7 0 3 5 1 𝟑 𝟓 𝟏 𝟐 𝟎 −𝟏 , 𝟐 −𝟒 𝟓 −2 −5 2 −2 2 5 −4 11 −5 •The expressions A+C, B+C and B-C are undefined. • Example If Then find A+B, B+A and A+2B. We have (by Rule 2). Also A+B = B+A • The difference of two matrices is written as which is interpreted as A - B, A + (-1) B, • Example: Find A - B, 2A - 3B if: and The rules of arithmetic as applied to the elements of matrices lead to the following results for matrices for which addition can be defined: Problems: Find B – C, 2B – 3C, C + B if: and Thanks