* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 13_2AnglesRadianMeas..
Survey
Document related concepts
Transcript
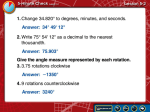
13.2 Angles of Rotation and Radian Measure ©2002 by R. Villar All Rights Reserved Angles of Rotation and Radian Measure In the last section, we looked at angles that were acute. In this section, we will look at angles of rotation whose measure can be any real number. An angle of rotation is formed by two rays with a common y endpoint (called the vertex). terminal side One ray is called the initial side. The other ray is called the terminal side. The measure of the angle is determined by the amount and direction of rotation from the initial side to the terminal side. vertex initial side The angle measure is positive if the rotation is counterclockwise, and negative if the rotation is clockwise. A full revolution (counterclockwise) corresponds to 360º. x Example: Draw an angle with the given measure in standard position. Then determine in which quadrant the terminal side lies. A. 210º b. –45º c. 510º 150º 210º –45º Terminal side is in Quadrant III Terminal side is in Quadrant IV 510º Terminal side is in Quadrant II Use the fact that 510º = 360º + 150º. So the terminal side makes 1 complete revolution and continues another 150º. 510º and 150º are called coterminal (their terminal sides coincide). An angle coterminal with a given angle can be found by adding or subtracting multiples of 360º. You can also measure angles in radians. One radian is the measure of an angle in standard position whose terminal side intercepts an arc of length r. r r one radian Since the circumference of a circle is 2πr, there are 2π radians in a full circle. Degree measure and radian measure are therefore related by the following: 360º = 2π radians Conversion Between Degrees and Radians • To rewrite a degree measure in radians, multiply by π radians 180º • To rewrite a radian measure in degrees, multiply by 180º π radians Examples: a. 240º Rewrite each in radians b. –90º 4 240º = 240º • π –90º = –90º • π 180º 180º 3 = –π = 4π 2 3 c. 135º 3 135º = 135º • π 180º 4 = 3π 4 240º = 4π radians 3 135º = 3π radians 4 –90º = –π radians 2 Examples: a. 5π 8 Rewrite each in degrees b. 16π 5 5π = 5π • 180º 8 8 π = 112.5º 16π = 16π • 180º 5 5 π = 576º Two positive angles are complementary if the sum of their measures is π/2 radians (which is 90º) Two positive angles are supplementary if the sum of their measures is π radians (which is 180º). Example: Find the complement of = π The complement is π – π 8 2 8 = 4π – π = 3π 8 8 8 Example: Find the supplement of = 3π The supplement is π – 3π 5 5 = 5π – 3π 5= 2π 5 5