Download 13_2AnglesRadianMeas..

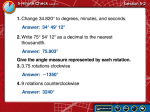
13.2 Angles of Rotation and
Radian Measure
©2002 by R. Villar
All Rights Reserved
Angles of Rotation and Radian Measure
In the last section, we looked at angles that were acute. In this
section, we will look at angles of rotation whose measure can be
any real number.
An angle of rotation is formed by two rays with a common
y
endpoint (called the vertex).
terminal side
One ray is called the initial side.
The other ray is called the terminal side.
The measure of the angle is determined by the
amount and direction of rotation from the
initial side to the terminal side.
vertex
initial side
The angle measure is positive if the rotation is counterclockwise,
and negative if the rotation is clockwise.
A full revolution (counterclockwise) corresponds to 360º.
x
Example:
Draw an angle with the given measure in standard
position. Then determine in which quadrant the terminal side lies.
A. 210º
b. –45º
c. 510º
150º
210º
–45º
Terminal side is in
Quadrant III
Terminal side is in
Quadrant IV
510º
Terminal side is in
Quadrant II
Use the fact that 510º = 360º + 150º.
So the terminal side makes 1
complete revolution and
continues another 150º.
510º and 150º are called coterminal (their terminal sides coincide).
An angle coterminal with a given angle can be found by adding or
subtracting multiples of 360º.
You can also measure angles in radians.
One radian is the measure of an angle in standard position whose
terminal side intercepts an arc of length r.
r
r
one radian
Since the circumference of a circle is 2πr, there
are 2π radians in a full circle.
Degree measure and radian measure are
therefore related by the following:
360º = 2π radians
Conversion Between Degrees and Radians
• To rewrite a degree measure in radians, multiply by π radians
180º
• To rewrite a radian measure in degrees, multiply by
180º
π radians
Examples:
a.
240º
Rewrite each in radians
b. –90º
4
240º = 240º • π
–90º = –90º • π
180º
180º
3
= –π
= 4π
2
3
c. 135º
3
135º = 135º • π
180º
4
= 3π
4
240º = 4π radians
3
135º = 3π radians
4
–90º = –π radians
2
Examples:
a.
5π
8
Rewrite each in degrees
b.
16π
5
5π = 5π • 180º
8
8
π
= 112.5º
16π = 16π • 180º
5
5
π
= 576º
Two positive angles are complementary if the sum of their measures is π/2 radians
(which is 90º)
Two positive angles are supplementary if the sum of their measures is π radians
(which is 180º).
Example: Find the complement of  = π
The complement is π – π
8
2
8
= 4π – π = 3π
8
8
8
Example: Find the supplement of  = 3π The supplement is π – 3π
5
5
= 5π – 3π 5= 2π
5
5