Download Heron`s Formula - cjmathemagician

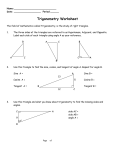
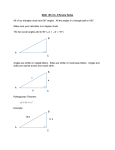
Jessica’s Take on
Modern Trigonometric Functions
and Their Uses
Jessica Smith
Heron’s Formula
• Formula used for finding the area (A) of
•
•
•
•
triangles.
Named after the Greek mathematician Heron
of Alexandria (ca. 100 B.C.)
He is believed to be real.
The formula is: A = (s(s-a)(s-b)(s-c)) where
S=(a+b+c) / 2
This formula only works if given all three sides
of any triangle.
The Wonderful World
of Reference Angles
• Values of trig functions of angles
greater than 90° are determined
from their values at corresponding
angles called reference angles.
• The reference angles are
determined by the acute angles
formed by the terminal side of the
angle and the horizontal axis.
• The original angle is represented
by  where the reference angle is
represented as ’.
All Students Take Calculus
• All Students Take Calculus is
an analogy used to help
determine the sign (positive
or negative) of the six
trigonometric functions.
• Used only in a rectangular
coordinate system with
quadrants I, II, III, and IV.
• Used starting in quadrant I
and moving one word at a
time, in the counterclockwise direction.
Law Of Cosines
c²= a² + b² – 2ab*cosC
C=27°
a=12
b=10
When you have a triangle with
two known sides and an angle
opposite the unknown side, you
can use the law of cosines to
find the length of the third side.
c=?
•c²= 12² + 10² - 2(12)(10)[ cos(27°)]
•c²= 244-240[cos(27°)]
•c²= 30.16
•c= 5.49
[cos(27°)] = 0.891
• SOH
– S=O/H
• S=Sine
• O=Opposite
• H=Hypotenus
e
• CAH
– C=A/H
• C=Cosine
• A=Adjacent
• H=Hypotenus
e
• TOA
– T=O/P
•
Soh-Cah-Toa- an analogy used to easily find
which numbers are used in the sine, cosine,
and tangent formulas in order to find angles.
• T=Tangent
• O=Opposite
• A=Adjacent
Cosine Graphs
• Horizontal value
Cosine Graph
– The degree value
• Vertical value
Cosine(x)
2
– Cosine x horizontal
value
1
0
-1 0
100
200
-2
Degree Value
300
400
Sine Graphs
• Horizontal Value
Sine Graph
– Degree Value
2
– Sine x
Horizontal Value
Sine (x)
• Vertical Value
1
0
-1 0
100
200
-2
Degree Value
300
400
Applying Trigonometry
Micaiah Bergeron
9
Have you ever needed to
convert radians to degrees or
vice versa?
•
•
•
•
•
Don’t flip out converting from rads to degs is easy as π.
To convert degrees to radians multiply degrees by (π/180)
To convert radians to degrees multiply radians by
(180/ π)
To convert 5 π/6 to degrees you would multiply the radian
measure by (180/ π) and you end up with 150 degrees.
To convert 30 degrees to radians multiply the degrees by
(π/180) and you end up with π/6 pie rads.
5 π X 180
30 X (π /180)= π/6
6
π
=150
10
Law of Sines
•
•
•
•
If you’ve made it this far in Trigonometry you know an
angle goes with its opposite side.
But did you know that all sinθ/side lengths
are congruent I mean angles and opposite sides go together.
You should apply law of sines when you have a triangle
ASA, AAS. You can use the law of sines for all triangles.
To find the other angle add the two you have and subtract
from 180. Put one side sinθ/side length = another side
sinθ/side length cross multiply and solve you may need to
use sin inverse to get the angle measure. Use this easy
formula for all parts of a triangle.
11
Translations of sine graphs
•
•
•
•
•
•
•
•
Translations of sine graphs are easy if you know what your looking
at and what the general shape and numbers are in a sine graph
The standard equation for a sine graph is:
y=a*sin b(x-c) + d
A= the amplitude of the graph.
B= the adjustment to the period, based on the standard 2 period.
C= the horizontal shift (negative numbers go right, positive numbers
go left)
D= the vertical shift of the graph ( positive numbers shift up and
negative numbers shift down)
Sample: y=2*sin 3(x+4) –3
Your amplitude is |2| your new period is 2/3 translate left 4 and
shift 3 down
12
Thank You!
Come Again!