Download Ratio Based on Right Triangles

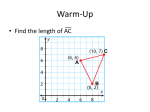
Math 10
Ms. Albarico
5.1 Ratios Based on Right Triangles
A. Modeling Situations Involving Right
Triangles
B. Congruence and Similarity
Students are expected to:
1) Apply the properties of similar triangles.
2) Solve problems involving similar triangles and right
triangles.
3) Determine
measurement.
the
accuracy
and
precision
of
a
4) Solve problems involving measurement using bearings
vectors.
Vocabulary
perpendicular
parallel
sides
angle
triangle
congruent
similar
dilate
sail
navigate
approach
Introduction
Triangles Around Us
Review
• Types of Triangles (Sides)
• a) Scalene
• b) Isosceles
• c) Equilateral
Review
• Types of Triangles (Angles)
• a) Acute
• b) Right
• c) Obtuse
• The most important skill you need right
now is the ability to correctly label the
sides of a right triangle.
• The names of the sides are:
– the hypotenuse
– the opposite side
– the adjacent side
Labeling Right Triangles
• The hypotenuse is easy to locate
because it is always found across from
the right angle.
Since this side is
across from the right
angle, this must be
the hypotenuse.
Here is the
right angle...
Labeling Right Triangles
• Before you label the other two sides you
must have a reference angle selected.
• It can be either of the two acute angles.
• In the triangle below, let’s pick angle B
as the reference angle.
B
A
This will be our
reference angle...
C
Labeling Right Triangles
• Remember, angle B is our reference
angle.
• The hypotenuse is side BC because it is
across from the right angle.
B (ref. angle)
hypotenuse
A
C
Labeling Right Triangles

Side AC is across from our reference angle
B. So it is labeled: opposite.
B (ref. angle)
hypotenuse
A
C
opposite
Labeling Right Triangles
Adjacent means beside or next to

The only side unnamed is side AB. This
must be the adjacent side.
B (ref. angle)
adjacent
hypotenuse
C
A
opposite
Labeling Right Triangles
• Let’s put it all together.
• Given that angle B is the reference
angle, here is how you must label the
triangle:
B (ref. angle)
hypotenuse
adjacent
C
A
opposite
Labeling Right Triangles
• Given the same triangle, how would the
sides be labeled if angle C were the
reference angle?
• Will there be any difference?
Labeling Right Triangles
• Angle C is now the reference angle.
• Side BC is still the hypotenuse since it
is across from the right angle.
B
hypotenuse
A
C (ref. angle)
Labeling Right Triangles

However, side AB is now the side opposite
since it is across from angle C.
B
opposite
hypotenuse
A
C (ref. angle)
Labeling Right Triangles

That leaves side AC to be labeled as the
adjacent side.
B
hypotenuse
opposite
A
C (ref. angle)
adjacent
Labeling Right Triangles
Let’s put it all together.
 Given that angle C is the reference angle,
here is how you must label the triangle:

B
hypotenuse
opposite
C (ref. angle)
A
adjacent
Labeling Practice
• Given that angle X is the reference
angle, label all three sides of triangle
WXY.
• Do this on your own. Click to see the
answers when you are ready.
W
Y
X
Labeling Practice
• How did you do?
• Click to try another one...
W
adjacent
opposite
hypotenuse
Y
X
Labeling Practice
• Given that angle R is the reference
angle, label the triangle’s sides.
• Click to see the correct answers.
R
T
S
Labeling Practice
• The answers are shown below:
R
hypotenuse
adjacent
T
opposite
S
Which side will never be the reference angle?
The right angle
What are the labels?
Hypotenuse, opposite, and adjacent
The Meaning of Congruence
A Congruent Figures
B Transformation and
Congruence
C Congruent Triangles
Conditions for Triangles to be
Congruent
A Three Sides Equal
B Two Sides and Their Included
Angle Equal
C Two Angles and One Side Equal
D Two Right-angled Triangles with
Equal Hypotenuses and Another
Pair of Equal Sides
The Meaning of Congruence
 Example
A)
Congruent Figures
1. Two figures having the same shape and the same size
are called congruent figures.
E.g. The figures X and Y as shown are congruent.
X
Y
2. If two figures are congruent, then they will fit exactly
on each other.
The Meaning of Congruence
The figure on the right shows a symmetric
figure with l being the axis of symmetry.
Find out if there are any congruent figures.
The line l divides the figure into 2 congruent figures,
i.e.
and
are congruent figures.
Therefore, there are two congruent figures.
The Meaning of Congruence
Find out by inspection the congruent figures among the following.
A
B
C
D
E
F
G
H
B, D ; C, F
The Meaning of Congruence
 Example
B)
Transformation and Congruence
‧
When a figure is translated, rotated or reflected, the
image produced is congruent to the original figure.
When a figure is enlarged or reduced, the image
produced will NOT be congruent to the original one.
Note:
A DILATATION is a transformation
which enlarges or reduces a shape but
does not change its proportions.
SIMILARITY is the result of dilatation.
"≅" means "is congruent to "
"~" is "similar to".
The Meaning of Congruence
In each of the following pairs of figures, the red one is obtained by
transforming the blue one about the fixed point x. Determine
(i) which type of transformation (translation, rotation, reflection,
enlargement, reduction) it is,
(ii) whether the two figures are congruent or not.
(a)
Reflection
(i) ____________
Yes
(ii) ____________
Index
The Meaning of Congruence
 Back to Question
(b)
Translation
(i) ____________
Yes
(ii) ____________
(c)
Enlargement
(i) ____________
No
(ii) ____________
Index
The Meaning of Congruence
 Back to Question
(d)
Rotation
(i) ____________
Yes
(ii) ____________
(e)
Reduction
(i) ____________
No
(ii) ____________
The Meaning of Congruence
 Example
C) Congruent Triangles
‧ When two triangles are congruent, all their corresponding
sides and corresponding angles are equal.
E.g. In the figure, if △ABC  △XYZ,
C
then
∠A = ∠X,
AB = XY,
∠B = ∠Y,
and BC = YZ,
∠C = ∠Z,
CA = ZX.
A
B
Z
X
Y
Trigonometry
Name a pair of congruent triangles in the figure.
From the figure, we see that △ABC  △RQP.
Trigonometry
Given that △ABC  △XYZ in the figure, find the unknowns
p, q and r.
For two congruent triangles, their corresponding sides and
angles are equal.
∴
∴ p = 6 cm ,
q = 5 cm , r = 50°
Trigonometry
Write down the congruent triangles in each of the following.
(a)
Y
A
Z
(b)
T
P
U
S
B
C
(a) △ABC  △XYZ
X
Q
R
(b) △PQR  △STU
Trigonometry
Find the unknowns (denoted by small letters) in each of the
following.
(a) △ABC  △XYZ
(b) △MNP  △IJK
X
P
A
i
98°
15
z
35°
C
13
Z
N
x
Y
M
j
J
(a) x = 14 , z = 13
K
47°
14
B
I
(b) j = 35° , i = 47°
Conditions for Triangles to be Congruent
 Example
A)
Three Sides Equal
‧
If AB = XY, BC = YZ and CA = ZX,
then △ABC  △XYZ.
A
X
【Reference: SSS】
B
C
Y
Z
Conditions for Triangles to be Congruent
Determine which pair(s) of triangles in the following are congruent.
(I)
(II)
(III)
In the figure, because of SSS,
(I) and (IV) are a pair of congruent triangles;
(II) and (III) are another pair of congruent triangles.
(IV)
Conditions for Triangles to be Congruent
Each of the following pairs of triangles are congruent. Which
of them are congruent because of SSS?
A
5
B
10
3
18
5
18
7
10
B
7
3
Conditions for Triangles to be Congruent
 Example
B)
Two Sides and Their Included Angle Equal
‧
If AB = XY, ∠B = ∠Y and BC = YZ,
then △ABC  △XYZ.
A
X
【Reference: SAS】
B
C
Y
Z
Conditions for Triangles to be Congruent
Determine which pair(s) of triangles in the following are congruent.
(I)
(II)
(III)
In the figure, because of SAS,
(I) and (III) are a pair of congruent triangles;
(II) and (IV) are another pair of congruent triangles.
(IV)
Conditions for Triangles to be Congruent
In each of the following figures, equal sides and equal angles
are indicated with the same markings. Write down a pair of
congruent triangles, and give reasons.
(a)
(a) △ABC  △CDA (SSS)
(b) △ACB  △ECD (SAS)
(b)
Conditions for Triangles to be Congruent
 Example
C)
Two Angles and One Side Equal
1. If ∠A = ∠X, AB = XY and ∠B = ∠Y,
then △ABC  △XYZ.
C
Z
【Reference: ASA】
A
B X
Y
Conditions for Triangles to be Congruent
 Example
C)
Two Angles and One Side Equal
2. If ∠A = ∠X, ∠B = ∠Y and BC = YZ,
then △ABC  △XYZ.
C
Z
【Reference: AAS】
A
B X
Y
Conditions for Triangles to be Congruent
Determine which pair(s) of triangles in the following are congruent.
(I)
(II)
(III)
In the figure, because of ASA,
(I) and (IV) are a pair of congruent triangles;
(II) and (III) are another pair of congruent triangles.
(IV)
Conditions for Triangles to be Congruent
In the figure, equal angles are indicated
with the same markings. Write down a
pair of congruent triangles, and give
reasons.
△ABD  △ACD (ASA)
Conditions for Triangles to be Congruent
1B_Ch11(53)
Determine which pair(s) of triangles in the following are congruent.
(I)
(II)
(III)
In the figure, because of AAS,
(I) and (II) are a pair of congruent triangles;
(III) and (IV) are another pair of congruent triangles.
(IV)
Conditions for Triangles to be Congruent
1B_Ch11(54)
In the figure, equal angles are indicated with the same
markings. Write down a pair of congruent triangles, and give
reasons.
D
A
B
△ABD  △CBD (AAS)
C
Conditions for Triangles to be Congruent
1B_Ch11(55)
 Example
D)
Two Right-angled Triangles with Equal Hypotenuses
and Another Pair of Equal Sides
‧
If ∠C = ∠Z = 90°, AB = XY and BC = YZ,
then △ABC  △XYZ.
A
X
【Reference: RHS】
B
C
Y
Z
Conditions for Triangles to be Congruent
Determine which of the following pair(s) of triangles are congruent.
(I)
(II)
(III)
In the figure, because of RHS,
(I) and (III) are a pair of congruent triangles;
(II) and (IV) are another pair of congruent triangles.
(IV)
Conditions for Triangles to be Congruent
In the figure, ∠DAB and ∠BCD are
both right angles and AD = BC.
Judge whether △ABD and △CDB
are congruent, and give reasons.
Yes, △ABD  △CDB (RHS)
The Meaning of Similarity
A Similar Figures
B Similar Triangles
Conditions for Triangles to be
Similar
A Three Angles Equal
B Three Sides Proportional
C Two Sides Proportional and
their Included Angle Equal
The Meaning of Similarity
 Example
A)
Similar Figures
1. Two figures having the same
shape are called similar figures.
The figures A and B as shown is
an example of similar figures.
2. Two congruent figures must be also similar figures.
3. When a figure is enlarged or reduced, the new figure is
similar to the original one.
The Meaning of Similarity
Find out all the figures similar to figure A by inspection.
A
D, E
B
C
D
E
The Meaning of Similarity
 Example
B)
Similar Triangles
1. If two triangles are similar, then
i. their corresponding angles are equal;
ii. their corresponding sides are proportional.
B
2. In the figure, if △ABC ~ △XYZ,
then ∠A = ∠X, ∠B = ∠Y,
∠C = ∠Z and
AB BC CA.


XY YZ ZX
A
C
Y
X
Z
The Meaning of Similarity
In the figure, given that △ABC ~ △PQR,
find the unknowns x, y and z.
x = 30° ,
∴
∴
y = 98°
QR
RP
=
BC
CA
z 4 .5
=
5
3
4.5
5
z=
3
= 7.5
The Meaning of Similarity
In the figure, △ABC ~ △RPQ. Find the values of the
unknowns.
Since △ABC ~ △RPQ,
∠B = ∠P
∴
x = 90°
The Meaning of Similarity
 Back to Question
Also,
BC
AB
=
PQ
RP
Also,
39
52
=
y
48
z
52
=
60
48
39 48
=y
52
∴
y = 36
AC
BC
=
RQ
PQ
52 60
z=
48
∴
z = 65
Conditions for Triangles to be Similar
 Example
A)
Three Angles Equal
‧
If two triangles have three pairs of
equal corresponding angles, then
they must be similar.
【Reference: AAA】
Conditions for Triangles to be Similar
Show that △ABC and △PQR in the
figure are similar.
In △ABC and △PQR as shown,
∠B = ∠Q, ∠C = ∠R,
∠A = 180° – 35° – 75° = 70°
∠P = 180° – 35° – 75° = 70°
∴ ∠A = ∠P
∴ △ABC ~ △PQR (AAA)
 ∠sum of 
Conditions for Triangles to be Similar
Are the two triangles in the figure similar? Give reasons.
【In △ABC, ∠B = 180° – 65° – 45° = 70°
In △PQR, ∠R = 180° – 65° – 70° = 45°】
Yes, △ABC ~ △PQR (AAA).
Conditions for Triangles to be Similar
 Example
B)
Three Sides Proportional
‧
If the three pairs of sides of two triangles are
proportional, then the two triangles must be similar.
【Reference: 3 sides proportional】
a
c
b
d
f
e
a b c
 
d e f
Conditions for Triangles to be Similar
Show that △PQR and △LMN
in the figure are similar.
In △PQR and △LMN as shown,
PQ
2 1
QR
3 1
RP
4 1
  ,
 


,
LM
8 4
MN 12 4
NL 16 4
PQ QR RP


∴
LM MN NL
∴ △PQR ~ △LMN (3 sides proportional)
Conditions for Triangles to be Similar
Are the two triangles in the figure similar? Give reasons.
AB 4
AC 12
BC 9
 2 ,

2 】
 2 ,
【
XZ 2
ZY 4.5
XY 6
Yes, △ABC ~ △XZY (3 sides proportional).
Conditions for Triangles to be Similar
 Example
C) Two Sides Proportional and their Included Angle Equal
‧
If two pairs of sides of two triangles are proportional
and their included angles are equal, then the two
triangles are similar.
【Reference: ratio of 2 sides, inc.∠】
p
r
x
q
y
s
p q
 , x y
r s
Conditions for Triangles to be Similar
Show that △ABC and △FED
in the figure are similar.
In △ABC and △FED as shown,
∠B = ∠E
AB 4
BC 9
 2 ,

2
FE 2
ED 4.5
AB BC

FE ED
∴
∴ △ABC ~ △FED (ratio of 2 sides, inc.∠)
Conditions for Triangles to be Similar
Are the two triangles in the figure similar? Give reasons.
【 ∠ZYX = 180° – 78° – 40° = 62°, ∠ZYX = ∠CBA = 62°,
BC 6
AB 4
 2 ,
 2 】
YZ 3
XY 2
Yes, △ABC ~ △XYZ (ratio of 2 sides, inc.∠).
Assignment
• Perform Investigation 1 on page 213-214
Homework:
• CYU # 6-11 on pages 215-216.
• Bring protractor next meeting!
WHAT IS A VECTOR?
It describes the motion of an object.
A Vector comprises of
– Direction
– Magnitude (Size)
We will consider :
– Column Vectors
Column Vectors
Vector a
a
4 RIGHT
(4, 2)
2 up
Column Vectors
Vector b
2 up
b
( -3, 2 )
3 LEFT
COLUMN
Vector?
Column Vectors
Vector u
n
( -4, -2 )
2 down
4 LEFT
COLUMN
Vector?
Describing Vectors
c
b
a
d
Alternative Labelling
B
F
EF
D
E
AB CD
G
C
A
H
GH
Generalization
Vectors has both LENGTH and
DIRECTION.
What is BEARINGS?
It is the angle of direction clockwise
from north.
Bearings
Ex.
The bearing of R from P is 220 and R is due west
of Q. Mark the position of R on the diagram.
Solution:
P
x
x
Q
Ex.
The bearing of R from P is 220 and R is due west
of Q. Mark the position of R on the diagram.
Solution:
P
x
.
x
Q
Ex.
The bearing of R from P is 220 and R is due west
of Q. Mark the position of R on the diagram.
Solution:
P
.
x
220
x
Q
If you only have a semicircular protractor, you need to
subtract 180 from 220 and measure from south.
Ex.
The bearing of R from P is 220 and R is due west
of Q. Mark the position of R on the diagram.
Solution:
P
x
. 40
x
Q
If you only have a semicircular protractor, you need to
subtract 180 from 220 and measure from south.
Ex.
The bearing of R from P is 220 and R is due west
of Q. Mark the position of R on the diagram.
Solution:
P
x
220
.
R
x
Q
Classwork
1) Answer the hand out given by the teacher.
2) Submit your work at the end of the class.
This will be evaluated. Make sure your scale drawing
is accurate and precise.
Homework:
1) Research about Pythagorean
Theorem and its proof.
2) Answer the following questions:
Check Your Understanding
# 14, 15, 16 on pages 218.
Vectors and Bearings