Download 2 Options: = or 180

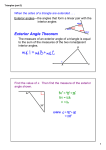
GEOMETRY
SOL IDEAS
Complementary angles
have the sum of 90.
Angles that form a LINEar
pair are supplementary (180).
Vertical angles are opposite
each other. They are equal.
Constructions (Use tracing paper!)
paper ruler, plastic compass
1. Segment / Angle Bisector
2. Congruent Segments / Angles
3. Perpendicular lines (90 degrees)
4. Perpendicular bisector
ISOSCELES
Venn Diagrams
EQUI
intersection = common
no intersection  nothing in
common
Circle inside another circle
“All bulldogs are dogs.”
Conditional (p  q)
Converse (q  p) switch
Inverse (p  q) not-not
Contrapositive (q  p)
Symbolic Representation
p: the opposite of p
Parallel Lines
(only 2 Options: = or 180)
alternate interior angles ( = ) Zorro
alternate exterior angles ( = )
corresponding angles ( = )
consecutive interior angles (180)
Parallel lines have EQUAL slopes.
Perpendicular lines have ‘opposite
reciprocal’ slopes. 2/3 & -3/2
Compute SLOPES visually.
from left to right,
count rise over run.
Triangle Sum Theorem
The sum of the 3 angles is 180.
An equilateral triangle is always a
60-60-60 triangle.
An equilateral triangle is isosceles.
(3 = sides means 2 = sides)
The base angles of an isosceles
triangle are congruent. (BAT)
Ext. Angle Theorem:
out = in + in
SAS, SSS, ASA, AAS (no SSA)
Use ticks & arcs.
Triangle Inequality Ideas
The bigger the angle, the longer
the opposite side, & vice-versa.
Draw and label a figure!
S, M, L
or L, M, S
Arrange from least to greatest,
greatest to least… (be careful!)
Triangle Inequality Theorem
sum of 2 shorter sides > 3rd
side
Technique:
Add 2 sides, Subtract 2 sides
(This gives the possible values
for 3rd side.)
Similar triangles: corresponding sides
are proportional (EQ: ratio = ratio)
S/S = M/M = L/L
Corresponding angles are congruent.
The sequence of letters is important!
Proportionality Theorems
part / part = part / part
(for any two SIMILAR figures)
ratio of perimeters = scale factor
(ratio of sides)
Pythagorean Theorem
Pythagorean Triples (5,12,13 ;
7, 24, 25 ; 3, 4, 5 ; etc.)
The altitude drawn to the
hypotenuse gives rise to THREE
similar triangles. (tic-tac-toe)
Special Right Triangles (shortcuts)
1. 45-45-90 (half-square)
legs are =
a  c: multiply by sq. rt. of 2
2. 30-60-90
a  c: multiply by 2
a  b: multiply by sq. rt. of 3
Trigonometry
[Degree Mode!!]
3 steps:
Label the sides. (eyeball)
EQ: SOH-CAH-TOA
Cross-multiply
elevation =
depression
Zorro
COODies for Parallelograms
(Set up equation based on these
properties.)
Special Properties
Diagonals of a rhombus
are perpendicular.
Diagonals of a rectangle are =.
Transformations or Movements
(translation, rotation, reflection)
‘slide’
‘turn’
‘flip’
Symmetry Lines for Polygons
regular polygons  ‘n’ sides
Point Symmetry (hexagon, S, O, N)
(when you turn by 180, you get same picture)
Rotation: Center & Angle
(connect technique)
Reflection: Across Different Axes
Translation: sliding an object
Images of Points (X, Y, Z  X’, Y’, Z’)
Watch out for the correspondence!
Tangents & Ice Cream Cones
Tangent line is perpendicular to
the radius. Use P.T.
Angle-Arc Relationships
1. Central Angle = Opposite Arc
2. Inscribed Angle is ½ of Arc
180 and 360 degree principles
Semi-circle = 180 (diameter)
Inscribed angle that cuts a
semi-circle = 90 (L-shape)
Segment relationships
(part)(part) = (part)(part)
(out)(total) = (out)(total)
tangent squared = (out)(total)
Other angle-arc relationships
in: (BIG + SMALL) / 2
(x – 2)^2 + (y + 5)^2 = 16
Center: (2, -5) and radius r = 4
Polygon Formulas (MEMORIZE)
(n – 2)(180)  sum of interior angles
Divide the above by n 
measure of EACH interior angle
(regular polygons)
n  number of sides
(also the number of angles)
360  sum of exterior angles
360 / n  each exterior angle
360 / ext. angle  n (sides)
The exterior & interior angles of
any polygon add up to 180.
(‘extend a side’ technique)
Areas of Similar Polygons
(ratio of sides) squared
Circumference and Arc Length
divide angle by 360 first
Areas of Sectors (pizza slice)
divide angle by 360 first
Then multiply…
3 dimensional figures
(scaling, fitting in a piece, nets)
3 perspective views
(top, side, front)
 use common sense!
Surface Area and Volume
Formulas (5 solids)
Use Formula Sheet!
B  area of base (8 x 8)
h  height
l  slant height (use P.T.)
r  radius (half of diameter)
Similar Figures / Solids
Ratio of Sides = Scale Factor
Ratio of Areas (squared/squared)
if scale is 2:3, then areas ratio is 4:9
Ratio of Volumes (cubed/cubed)
if scale is 2:3, then volumes ratio is 8:27
Some problems don’t require the use
of formula sheet. Set up ratio = ratio.
Label points first!
(x1,y1) & (x2,y2)
Use techniques shown in class.
Slope:
Distance:
Midpoint: add & divide by 2
Good Luck!
Give it your best shot!
(time incentive)