Download Exterior Angles and Triangles

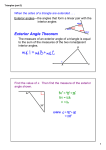
4.2 Angles of Triangles
Objectives
Apply the Angle Sum Theorem
Apply the Exterior Angle Theorem
Theorem 4.1 – Angle Sum Theorem
The sum of the measures of the angles of a
triangle is 180°.
X
mX + mY + mZ = 180°
Y
Z
Example 1:
Find the missing angle measures.
Find
first because the
measure of two angles of
the triangle are known.
Angle Sum Theorem
Simplify.
Subtract 117 from each side.
Example 1:
Angle Sum Theorem
Simplify.
Subtract 142 from each side.
Answer:
Your Turn:
Find the missing angle measures.
Answer:
Theorem 4.2 – Third Angle Theorem
If two angles of one triangle are congruent
to two angles of a second triangle, then
the third angles of the triangle are
congruent.
Abbreviation: If 2 s of one Δ are  to 2 s
of another Δ, then third s are .
Exterior Angles and Triangles
An exterior angle is formed by one side of a
triangle and the extension of another side
(i.e. 1 ).
2
1
4
3
The interior angles of the triangle not adjacent to
a given exterior angle are called the remote
interior angles (i.e. 2 and 3).
Theorem 4.3 – Exterior Angle Theorem
The measure of an exterior angle of a
triangle is equal to the sum of the
measures of the two remote interior
angles.
m 1 = m 2 + m 3
2
1
4
3
Example 2:
Find the measure of each numbered angle in the figure.
Exterior Angle Theorem
Simplify.
If 2 s form a linear pair, they
are supplementary.
Substitution
Subtract 70 from each side.
Example 2:
Exterior Angle Theorem
Substitution
Subtract 64 from each side.
If 2 s form a linear pair,
they are supplementary.
Substitution
Simplify.
Subtract 78 from each side.
Example 2:
Angle Sum Theorem
Substitution
Simplify.
Subtract 143 from each side.
Answer:
Your Turn:
Find the measure of each numbered angle in the figure.
Answer:
Corollaries
A corollary is a statement that can be
easily proven using a theorem.
Corollary 4.1 – The acute s of a right ∆
are complementary.
Corollary 4.2 – There can be at most one
right or obtuse  in a ∆.
Example 3:
GARDENING The flower bed shown is in the shape of
a right triangle. Find
if
is 20.
Corollary 4.1
Substitution
Subtract 20 from each side.
Answer:
Your Turn:
The piece of quilt fabric is in the shape of a
right triangle. Find
if
is 32.
Answer:
Assignment
Geometry:
Pg. 189 #11 - 35
Pre-AP Geometry:
Pg. 189 #11 - 40