Download Lesson

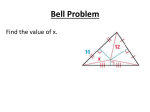
Lesson 5-1
Bisectors in Triangles
Transparency 5-1
5-Minute Check on Chapter 4
Refer to the figure.
1. Classify the triangle as scalene, isosceles, or equilateral.
2. Find x if mA = 10x + 15, mB = 8x – 18, and
mC = 12x + 3.
3. Name the corresponding congruent angles if
RST  UVW.
4. Name the corresponding congruent sides if LMN  OPQ.
5. Find y if DEF is an equilateral triangle and mF = 8y + 4.
6.
Standardized Test Practice:
What is the slope of a line that contains
(–2, 5) and (1, 3)?
A
–2/3
B
2/3
C
–3/2
D
3/2
Transparency 5-1
5-Minute Check on Chapter 4
Refer to the figure.
1. Classify the triangle as scalene, isosceles, or equilateral.
isosceles
2. Find x if mA = 10x + 15, mB = 8x – 18, and
mC = 12x + 3.
6
3. Name the corresponding congruent angles if
RST  UVW.
R  U; S  V; T  W
4. Name the corresponding congruent sides if LMN  OPQ.
LM  OP; MN  PQ; LN  OQ
5. Find y if DEF is an equilateral triangle and mF = 8y + 4.
6.
Standardized Test Practice:
What is the slope of a line that contains
(–2, 5) and (1, 3)?
A
–2/3
B
2/3
7
C
–3/2
D
3/2
Objectives
• Identify and use perpendicular bisectors in
triangles
• Identify and use angle bisectors in triangles
Vocabulary
• Concurrent lines – three or more lines that intersect at
a common point
• Point of concurrency – the intersection point of three or
more lines
• Perpendicular bisector – passes through the midpoint
of the segment (triangle side) and is perpendicular to
the segment
• Circumcenter – the point of concurrency of the
perpendicular bisectors of a triangle; the center of the
largest circle that contains the triangle’s vertices
• Incenter – the point of concurrency for the angle
bisectors of a triangle; center of the largest circle that
can be drawn inside the triangle
Theorems
• Theorem 5.1 – Any point on the perpendicular bisector of a
segment is equidistant from the endpoints of the segment.
• Theorem 5.2 – Any point equidistant from the endpoints of
the segments lies on the perpendicular bisector of a
segment.
• Theorem 5.3, Circumcenter Theorem – The circumcenter of
a triangle is equidistant from the vertices of the triangle.
• Theorem 5.4 – Any point on the angle bisector is equidistant
from the sides of the triangle.
• Theorem 5.5 – Any point equidistant from the sides of an
angle lies on the angle bisector.
• Theorem 5.6, Incenter Theorem – The incenter of a triangle
is equidistant from each side of the triangle.
Triangles – Perpendicular Bisectors
A
Note: from Circumcenter
Theorem: AP = BP = CP
Z
Midpoint
of AC
Circumcenter
Midpoint
of AB X
P
C
Y
Midpoint
of BC
B
Circumcenter is equidistant from the vertices
Perpendicular Bisector Theorems
Example 1A
A. Find BC.
From the information in the
diagram, we know that line CD is
the perpendicular bisector of line
segment AB.
BC = AC
Perpendicular Bisector Theorem
BC = 8.5
Substitution
Answer: 8.5
Example 1B
B. Find XY.
Answer: 6
Example 1C
C. Find PQ.
From the information in the diagram, we
know that line QS is the perpendicular
bisector of line segment PR.
PQ = RQ
3x + 1 = 5x – 3
Substitution
1 = 2x – 3
Subtract 3x from each side.
4 = 2x
Add 3 to each side.
2 =x
Divide each side by 2.
So, PQ = 3(2) + 1 = 7.
Answer: 7
Perpendicular Bisector Theorem
Perpendicular Bisector Theorems
Example 2
• GARDEN A triangular-shaped garden is
shown. Can a fountain be placed at the
circumcenter and still be inside the garden?
By the Circumcenter Theorem, a
point equidistant from three
points is found by using the
perpendicular bisectors of the
triangle formed by those points.
Copy ΔXYZ, and use a ruler and
protractor to draw the
perpendicular bisectors. The
location for the fountain is C, the
circumcenter of ΔXYZ, which lies
in the exterior of the triangle.
Answer: No, the circumcenter of an obtuse triangle is
in the exterior of the triangle.
Triangles – Angle Bisectors
A
Note: from Incenter Theorem:
QX = QY = QZ
Z
Q
Incenter
C
X
Y
B
Incenter is equidistant from the sides
Angle Bisector Theorems
Example 3A
A. Find DB.
From the information in the
diagram, we know that ray AD is
the angle bisector of  BAC.
DB = DC
Angle Bisector Theorem
DB = 5
Substitution
Answer: 5
Example 3B
B. Find mWYZ.
Answer: mWYZ = 28°
Example 3C
C. Find QS.
QS = SR
4x – 1 = 3x + 2
x–1 =2
x =3
Angle Bisector Theorem
Substitution
Subtract 3x from each side.
Add 1 to each side.
Answer: QS = 4(3) – 1 = 11
Angle Bisector Theorems
Example 4A
A. Find ST if S is the incenter of ΔMNP.
By the Incenter Theorem, since S is
equidistant from the sides of ΔMNP,
ST = SU.
Find ST by using the
Pythagorean Theorem.
a2 + b2 = c2
Pythagorean Theorem
82 + SU2 = 102
Substitution
64 + SU2 = 100
82 = 64, 102 = 100
SU2 = 36
SU = 6
Answer: ST = SU = 6
subtract 36 from both sides
positive square root
Example 4B
B. Find mSPU if S is the incenter
of ΔMNP.
Since NR and MU are angle bisectors,
we double the given half-angles to get
the whole angles in:
mUPR + mRMT + mTNU = 180
mUPR + 62 + 56 = 180
mUPR + 118 = 180
mUPR = 62
Triangle Angle
Sum Theorem
Substitution
Simplify.
Subtract 118
from each side.
Answer: mSPU = (1/2) mUPR = 31
Example 5
Given:
Find:
mDGE
2x + 80 + 30 = 180
2x + 110 = 180
2x = 70
x = 35
x + mDGE + 30 = 180
35 + mDGE + 30 = 180
mDGE + 65 = 180
mDGE = 115
3 ’s in triangle sum to 180
subtracting 110 from both sides
dividing both sides by 2
3 ’s in triangle sum to 180
substitute x
combine numbers
subtract 65 from both sides
Special Segments in Triangles
Name
Type
Point of
Concurrency
Perpendicular
Line,
Circumcenter
bisector
segment or
ray
Angle
bisector
Line,
segment or
ray
Incenter
Center Special
Quality
From
/ To
Equidistant
from vertices
None
midpoint of
segment
Equidistant
from sides
Vertex
none
Location of Point of Concurrency
Name
Point of Concurrency
Perpendicular bisector
Circumcenter
Angle bisector
Incenter
Triangle Classification
Acute
Right
Obtuse
Inside hypotenuse Outside
Inside
Inside
Inside
Summary & Homework
• Summary:
– Perpendicular bisectors and angle bisectors of a
triangle are all special segments in triangles
– Perpendiculars bisectors:
• form right angles
• divide a segment in half – go through midpoints
• equal distance from the vertexes of the triangle
– Angle bisector:
• cuts angle in half
• equal distance from the sides of the triangle
• Homework:
– pg 327-31; 1-3, 5-7, 9-11, 26-30