Download Geometry. - Cloudfront.net

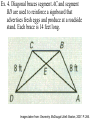
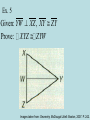
GEOMETRY: Chapter 4
4.6: Use Isosceles and Equilateral
Triangles
Theorem 4.6: BASE ANGLES THEOREM
If two sides of a triangle are congruent, then the
angles opposite them are congruent.
If AB  AC , then B  C.
Images taken from: Geometry. McDougal Littell: Boston, 2007. P. 264.
Theorem 4.7: CONVERSE OF BASE
ANGLES THEOREM
If the angles of a triangle are congruent,
then the sides opposite them are
congruent.
If B  C , then AB  AC.
Images taken from: Geometry. McDougal Littell: Boston, 2007. P. 264.
Ex. 1
In PQR, PQ  QR.
Name two congruent angles.
Images taken from: Geometry. McDougal Littell: Boston, 2007. P. 265.
Corollary to the Base Angles Theorem
If a triangle is equilateral, then it is
equiangular.
Corollary to the Converse of the Base
Angles Theorem
If a triangle is equiangular, then it is
equilateral.
Images taken from: Geometry. McDougal Littell: Boston, 2007. P. 265.
Ex. 2. Find the measures of X and Y.
Images taken from: Geometry. McDougal Littell: Boston, 2007. P. 265.
Ex. 3. Find the values of x and y in the diagram.
Images taken from: Geometry. McDougal Littell: Boston, 2007. P. 266.
Ex. 4. Diagonal braces segment AC and segment
BD are used to reinforce a signboard that
advertises fresh eggs and produce at a roadside
stand. Each brace is 14 feet long.
Images taken from: Geometry. McDougal Littell: Boston, 2007. P. 266.
Ex. 4. (cont.)
a. What congruence postulate can you use to
prove that triangle ABC is congruent to triangle
DCB?
b. Explain why triangle BEC is isosceles.
c. What triangles would you use to show that
triangle AED is isosceles?
RIGHT TRIANGLES—In a right triangle, the
sides adjacent to the right angle are called
the legs. The side opposite the right angle is
called the hypotenuse of the right triangle.
Images taken from: Geometry. McDougal Littell: Boston, 2007. P. 241.
Theorem 4.8 Hypotenuse-Leg (HL)
Congruence Theorem
If the hypotenuse and a leg of a right triangle
are congruent to the hypotenuse and a leg of
a second right triangle, then the two
triangles are congruent.
Images taken from: Geometry. McDougal Littell: Boston, 2007. P. 241.
Ex. 5
Given: YW  XZ , XY  ZY
Prove: XYZ  ZYW
Images taken from: Geometry. McDougal Littell: Boston, 2007. P. 242.
Write Ex. 5 Proof here:
Write Ex. 5 Proof here:
Triangle Congruence Postulates and Theorems
SSS
All three
sides are
congruent.
SAS
Two sides
and the
included
angle are
congruent.
HL
The
hypotenuse
and one of
the legs are
congruent.
(Right triangle only)
ASA
Two angles
and the
included
side are
congruent.
AAS
Two angles
and a nonincluded
side are
congruent.
Images taken from: Geometry. McDougal Littell: Boston, 2007. P. 252.