Download Lesson 1 Contents

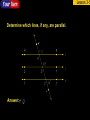
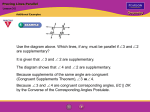
Lesson 3-5
Proving Lines Parallel
5-Minute Check on Lesson 3-4
Transparency 3-5
Write an equation in point-slope form for each line.
1. line with slope ¾ containing (5, –2)
2. line parallel to the line 3x – y = 6 that contains (–2, 7)
Write an equation in slope-intercept form for each line.
3. line with slope –3 containing (0, 2.5)
4. line with slope –1/2 containing (4, –6)
5. line through (1, 5) and (3, 11)
6.
Standardized Test Practice:
Which of the following describes the line
y = –2/3x + 6?
A
parallel to the line y = 3/2x + 6
B
perpendicular to the line y = –3/2x + 6
C
x-intercept is 6; y-intercept is 9
D
x-intercept is 9; y-intercept is 6
5-Minute Check on Lesson 3-4
Transparency 3-5
Write an equation in point-slope form for each line.
1. line with slope ¾ containing (5, –2) y + 2 = ¾(x – 5)
2. line parallel to the line 3x – y = 6 that contains (–2, 7)
y – 7 = 3(x + 2)
Write an equation in slope-intercept form for each line.
3. line with slope –3 containing (0, 2.5) y = –3x + 2.5
4. line with slope –1/2 containing (4, –6) y = –1/2x – 4
5. line through (1, 5) and (3, 11) y = 3x + 2
6.
Standardized Test Practice:
Which of the following describes the line
y = –2/3x + 6?
A
parallel to the line y = 3/2x + 6
B
perpendicular to the line y = –3/2x + 6
C
x-intercept is 6; y-intercept is 9
D
x-intercept is 9; y-intercept is 6
Objectives
• Recognize angle conditions that occur with
parallel lines
• Prove that two lines are parallel based on
given angle relationships
Vocabulary
• No new vocabulary words or symbols
t
Postulates & Theorems
To Prove Lines Parallel
k
3
l
5
7
1 2
4
6
8
Postulate/
Theorem
Statement
Examples
Postulate 3.4
If two lines in a plane are cut by a transversal so that
corresponding angles are congruent, then the lines are
parallel
If 1  5 or 2  6 or
3  7 or 4  8,
then k || l
Parallel
Postulate
If a given line and a point not on the line, then there
None illustrated
exists exactly one line through the point that is parallel to
the given line
Theorem 3.5
If two lines in a plane are cut by a transversal so that a
pair of alternate exterior angles are congruent, then the
lines are parallel
If 1  8 or 2  7,
then k || l
Theorem 3.6
If two lines in a plane are cut by a transversal so that a
pair of consecutive interior angles are supplementary,
then the lines are parallel
If m3 + m5 = 180° or
m4 + m6 = 180°, then
k || l
Theorem 3.7
If two lines in a plane are cut by a transversal so that a
pair of alternate interior angles are congruent, then the
lines are parallel
If 3  6 or 4  5,
then k || l
Determine which lines,
if any, are parallel.
consecutive
interior angles are supplementary. So,
consecutive
interior angles are not supplementary. So, c is not parallel
to a or b.
Answer:
Determine which lines, if any, are parallel.
Answer:
ALGEBRA Find x and mZYN so that
Explore From the figure, you know that
and
You also know that
are alternate exterior angles.
Plan For line PQ to be parallel to MN, the alternate exterior
angles must be congruent.
Substitute the given angle measures into this equation
and solve for x. Once you know the value of x, use
substitution to find
Solve
Alternate exterior angles
Substitution
Subtract 7x from each side.
Add 25 to each side.
Divide each side by 4.
Original equation
Simplify.
Examine Verify the angle measure by using the value of x to
find
Since
Answer:
ALGEBRA Find x and mGBA so that
Answer:
Answer:
Answer: Since the slopes are not equal, r is not parallel to s.
Summary & Homework
• Summary:
– When lines are cut by a transversal,
certain angle relationships produce
parallel lines
•
•
•
•
Congruent corresponding angles
Congruent alternate interior angles
Congruent alternate exterior angles
Supplementary consecutive interior angles
• Homework:
pg 154-155: 4, 7, 13-16, 27, 29, 31