* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Week 13 - Troy High School
Multilateration wikipedia , lookup
Euler angles wikipedia , lookup
Golden ratio wikipedia , lookup
Four color theorem wikipedia , lookup
Perceived visual angle wikipedia , lookup
History of trigonometry wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Trigonometric functions wikipedia , lookup
Rational trigonometry wikipedia , lookup
Euclidean geometry wikipedia , lookup
Incircle and excircles of a triangle wikipedia , lookup
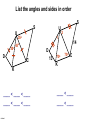
Week 13 5.6 – Indirect Proof and Inequalities in Two Triangles Hinge Theorem If two sides one triangle are congruent to two sides of another triangle, but the included angle of the first triangle is larger than the included angle of the second, then the third side of the first triangle is longer than the third side of the second triangle. Fancy talk for two sides same, one angle bigger than other, then side is bigger Given : BA ED, BC EF, D A mB mE Then : AC DF E B C F Converse of Hinge Theorem If two sides one triangle are congruent to two sides of another triangle, but the 3rd side of the first triangle is longer than the 3rd side of the second, then the included angle of the first triangle is larger than the included angle of the second. Fancy talk for two sides same, one sidee bigger than other, then angle is bigger Given : BA ED, BC EF, D A AC DF Then : mB mE E B C F List the angles and sides in order S S U 30o D U 35o 2 1 14 45o D C 13 70o 70o C K K ____ < ____ < ____ ____ < ____ ____ < ____ < ____ ____ < ____ student Indirect Proof How to write an indirect proof 1. Assume temporarily that the conclusion is not true. 2. Reason logically until you reach a contradiction of the known fact. 3. Point out the temporary assumption is false, so the conclusion must be true. Practice Write the untrue conclusion Prove : n is odd Prove : sum of interior angles of a triangle is 180 Prove : AB AB Prove : Mr. Kim is a genius a b 1 Given : m1 m3 3 Prove : a || b Given : m1 50, m2 60 Prove : 1 and 2 are not a linear pair a b 1 3 Given : 1, 3 not supp. Prove : a || b