Download 8-3 Proving Triangles Similar

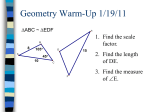
8-3
Proving Triangles Similar
One
Postulate
Two Theorems
Postulate 8-1
Angle-Angle Similarity (AA~) Postulate

If two angles of one triangle are congruent to
two angles of another triangle, then the triangles
are similar.
Theorem 8-1
Side-Angle-Side Similarity (SAS~) Theorem

If an angle of one triangle is congruent to an
angle of a second triangle, and the sides
including the two angles are proportional, then
the triangles are similar.
Theorem 8-2
Side-Side-Side Similarity (SSS~) Theorem

If the corresponding sides of two triangles are
proportional, then the triangles are similar.
#1 Using the Similarity Theorems
What theorem or postulate state
that the two triangles similar?
V
W
S
1.
R  V
2. WSR
3.
1.
Given
 VSB
2.
Vertical Angles
RWS ~ VSB
3.
AA ~ Postulate
450
450
R
B
#2 Using Similarity Theorems
 Write a similarity statement for the two triangles.
A
6
6 9
Small Triangle
 

8
8 12
Large Triangle
9
6
B
6
C
E
G
8
8
12
3 3 3
 
4 4 4
ABC ~ EFG because all sides have a 3 : 4 ratio.
F
#3 Finding Lengths in Similar Triangles
 Find the value of x in the figure.
6 8
Small Triangle


x 12
Large Triangle
6
8
6 8

x 12
6(12)  8 x
72  8x
x 9
12
x