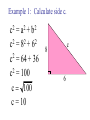Download Lesson 1

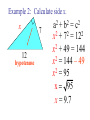
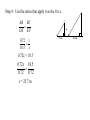
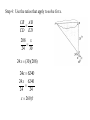
Triangle Review
A scalene triangle has no
sides and no angles equal.
An isosceles triangle has two
sides and two angles equal.
An equilateral triangle has three
sides and three angles equal.
A right triangle has one
right angle.
Identify the triangle below;
right isosceles
How are the three sides of a right triangle
related to each other?
The Pythagorean Theorem
2
2
2
a +b =c
c
a
b
Hypotenuse, the longest
side of a right triangle
Example 1: Calculate side c.
c2 = a 2 + b 2
2
2
2
c =8 +6
c2 = 64 + 36
2
c = 100
c  100
c = 10
c
8
6
Example 2: Calculate side x.
x
7
12
hypotenuse
2
a +
2
x +
2
b
2
7
2
c
=
2
= 12
2
x + 49 = 144
x2 = 144 – 49
2
x = 95
x  95
x = 9.7
Similar Triangles
Two triangles are considered
to be similar if and only if:
• they have the same shape
• corresponding angles are equal
• the ratio of the corresponding side
lengths are equal
F
C
Ex 1. Find x.
x
1m
A
B
72 cm
D
E
18.5 m
Step 1: Identify two similar triangles.
 ABC ~  DEF
Step 2: Write equivalent ratios
AB BC AC


DE EF DF
Step 4: Use the ratios that apply to solve for x.
C
AB BC

DE EF
x
1m
A
0.72 1

18.5 x
0.72x = 18.5
0.72 x 18.5

0.72 0.72
x = 25.7 m
F
B
72 cm
D
E
18.5 m
Ex #2: Surveyors have laid out
triangles to find the length of a lake.
Calculate this length, AB.
ft
Step 1: Draw a labeled diagram.
PROVIDED
Step 2: Identify two similar triangles.
 ACB ~  ECD
Step 3: Write equivalent ratios
AC CB AB


EC CD ED
ft
ft
Step 4: Use the ratios that apply to solve for x.
CB AB

CD ED
208 x

24 30
24 x  (30)( 208)
24x  6240
24 x 6240

24
24
x  260 ft
ft
ft
ft