Download journal 6 Delia

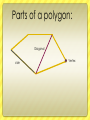
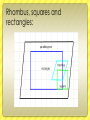
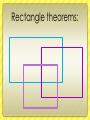
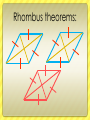
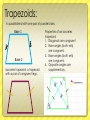
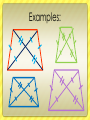
Journal 6:
Polygons
Delia Coloma 9-5
What is a polygon?
Sides:
3. Triangle
4. Quadrilateral
5. Pentagon
6. Hexagon
7. Heptagon
8. Octagon
9. Nonagon
10. Decagon
12. Dodecagon
• A Polygon is a 2dimensional shape
made up of
straight lines, and
closed. This means
that all the lines
need to connect .
Found example:
Parts of a polygon:
Diagonal
side
Vertex
Real life examples:
Concave vs. Convex
Convex:
It is when a polygon has
all vertices pointing
outwards.
Example 1)

Concave:
It is when any figure has
1 or more vertices
pointing inwards.

Example 1)
Example 2)
Example 3)
Example 2)
Example 3)
Real life example:
Concave:
Convex:
Equilateral vs. equiangular
Equilateral:
It is when all of the sides
are congruent.

1m
1m
1m
1m
1m
1m
14 cm
14 cm
2 in
2 in
2 in
2 in
14 cm
Equiangular:
It is when all of the
angles are congruent.

Real Life example:
Equilateral:
Equiangular:
Interior angles theorem for
polygons:
If it is a regular
polygon: To find
each interior angle,
you need to use this
formula:
N-2 x 180
Then divide by the
number of sides.
Examples:
Hexagon
Heptagon
6-2=4
4x180= 720
720/6=120
5-2=3
3x180=540
540/5=108
quadrilateral
4-2=2
2x180=360
360/4=90
Real life example:
6-2=4
4x180= 720
720/6=120
Theorems of Parallelograms:
1. Opposite sides are congruent
2. Definition of parallelogram: quadrilateral that has
opposite sides parallel to each other.
3. Opposite angles are congruent
4. Diagonals bisect each other
5. Consecutive angles are supplementary
6. It has one set of congruent and parallel sides.
Converse of theorems of
parallelograms:
1. If it is a parallelogram then opposite sides are
congruent
2. quadrilateral that has opposite sides parallel to
each other is a parallelogram
3. If their opposite angles are congruent, then it is a
parallelogram
4. The diagonals will bisect each other if it is a
parallelogram.
5. If the consecutive angles are supplementary then it
is a parallelogram
6. If it has one set of congruent and parallel sides, then
it is a parallelogram.
How to prove that quadrilateral is a
parallelogram…
b
c
2
Given: AB is congruent to CD, BC is
cong. To DA
Prove: ABCD is a parallelogram.
1
4
a
statement
reason
Ab is cong to cd, bc is
congr to da
given
Bd is cong to bd
Reflexive property
Triangle dab is cong to
dcb
sss
<1 is cong to <3, <4
is cong to <2
cpct
Ab || to cd, bc is || to
da
Abcd is a
parallelogram
Alternate int. Angles
tm
Def of parallelogram
3
d
Rhombus, squares and
rectangles:
Rectangles:
It is any parallelogram with 4 right
angles.
1. The diagonals bisect each other,
so they are congruent.
Example 1)
Example 3)
Example 2)
Real life example:
Rectangle theorems:
Theorem 6-5-1:
If one angle of a parallelogram is a right angle,
then the parallelogram is a rectangle.
Theorem 6-5-2:

If the diagonals of a parallelogram are congruent,
then the parallelogram is a rectangle.
Rhombus:
A parallelogram with 4
congruent sides.
1. Diagonals are perpendicular.
Example 1)
Example 3)
Example 2)
Real life example:
Rhombus theorems:
Theorem 6-5-3:
If one pair of consecutive sides of a parallelogram
are congruent, then the parallelogram is a
rhombus.
Theorem 6-5-4:
If the diagonals of a parallelogram are
perpendicular, then the parallelogram is a
rhombus.
Theorem 6-5-5:

If one diagonal of a parallelogram bisects a pair of
opposite angles, then the parallelogram is a
rhombus.
Squares:
A parallelogram that is both a rectangle and a
rhombus.
1) Has parallelogram characteristics.
“Cartoon life example:”
Trapezoids:
A quadrilateral with one pair of parallel sides.
Base 1
Base 2
Isosceles trapezoid: a trapezoid
with a pair of congruent legs.
Properties of an isosceles
trapezoid:
1. Diagonals are congruent
2. Base angles (both sets)
are congruent.
3. Base angles (both sets)
are congruent.
4. Opposite angles are
supplementary.
Examples:
Real life example:
Trapezoidal theorems:
Theorem 6-6-3

If a quadrilateral is an isosceles trapezoid, then
each pair of base angles are congruent.
Theorem 6-6-4

If a trapezoid has one pair of congruent base
angles, then the trapezoid isosceles.
Theorem 6-6-5:

A Trapezoid is isosceles if and only if its diagonals
are congruent.
Trapezoid midsegment
theorem:

The midsegment of a trapezoid is parallel to each base and
its length is one half the sum of the length of the bases.
Kite:
Has two pairs of congruent
adjacent sides.
1) Diagonals are
perpendicular
2) One pair of congruent
angles (the ones formed
by non-congruent sides)
3) One of the diagonals
bisects the other.
Examples:
Real life example:
Kite theorems:
Theorem 6-6-1:

If a quadrilateral is a kite, then its diagonals are
perpendicular.
Theorem 6-6-2:

If a quadrilateral is a kite, then exactly one pair of
opposite angles are congruent.
THE END (: