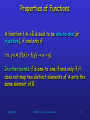Download Lecture notes for Chapter 1

Let’s get started with...
Logic!
Spring 2003
CMSC 203 - Discrete Structures
1
Logic
• Crucial for mathematical reasoning
• Important for program design
• Used for designing electronic circuitry
• Logic is a system based on propositions.
• A proposition is a (declarative) statement
that is either true or false (not both).
• We say that the truth value of a proposition
is either true (T) or false (F).
• Corresponds to 1 and 0 in digital circuits
Spring 2003
CMSC 203 - Discrete Structures
2
The Statement/Proposition Game
“Elephants are bigger than mice.”
Is this a statement?
yes
Is this a proposition?
yes
What is the truth value
of the proposition?
true
Spring 2003
CMSC 203 - Discrete Structures
3
The Statement/Proposition Game
“520 < 111”
Is this a statement?
yes
Is this a proposition?
yes
What is the truth value
of the proposition?
false
Spring 2003
CMSC 203 - Discrete Structures
4
The Statement/Proposition Game
“y > 5”
Is this a statement?
yes
Is this a proposition?
no
Its truth value depends on the value of y,
but this value is not specified.
We call this type of statement a
propositional function or open sentence.
Spring 2003
CMSC 203 - Discrete Structures
5
The Statement/Proposition Game
“Today is January 27 and 99 < 5.”
Is this a statement?
yes
Is this a proposition?
yes
What is the truth value
of the proposition?
false
Spring 2003
CMSC 203 - Discrete Structures
6
The Statement/Proposition Game
“Please do not fall asleep.”
Is this a statement?
no
It’s a request.
Is this a proposition?
no
Only statements can be propositions.
Spring 2003
CMSC 203 - Discrete Structures
7
The Statement/Proposition Game
“If the moon is made of cheese,
then I will be rich.”
Is this a statement?
yes
Is this a proposition?
yes
What is the truth value
of the proposition?
probably true
Spring 2003
CMSC 203 - Discrete Structures
8
The Statement/Proposition Game
“x < y if and only if y > x.”
Is this a statement?
yes
Is this a proposition?
yes
… because its truth value
does not depend on
specific values of x and y.
What is the truth value
of the proposition?
Spring 2003
CMSC 203 - Discrete Structures
true
9
Combining Propositions
As we have seen in the previous examples,
one or more propositions can be combined
to form a single compound proposition.
We formalize this by denoting propositions
with letters such as p, q, r, s, and
introducing several logical operators or
logical connectives.
Spring 2003
CMSC 203 - Discrete Structures
10
Logical Operators (Connectives)
We will examine the following logical operators:
• Implication
)
(AND, )
(OR, )
(XOR,  )
(if – then, 
)
• Biconditional
(if and only if,

• Negation
• Conjunction
• Disjunction
• Exclusive-or
(NOT,
)
Truth tables can be used to show how these
operators
can combine
propositions
to
Spring 2003
CMSC 203 - Discrete
Structures
compound propositions.
11
Negation (NOT)
Unary Operator, Symbol: 
Spring 2003
P
 P
true (T)
false (F)
false (F)
true (T)
CMSC 203 - Discrete Structures
12
Conjunction (AND)
Binary Operator, Symbol: 
Spring 2003
P
Q
P Q
T
T
T
T
F
F
F
T
F
F
F
F
CMSC 203 - Discrete Structures
13
Disjunction (OR)
Binary Operator, Symbol: 
Spring 2003
P
Q
P Q
T
T
T
T
F
T
F
T
T
F
F
F
CMSC 203 - Discrete Structures
14
Exclusive Or (XOR)
Binary Operator, Symbol: 
Spring 2003
P
Q
P Q
T
T
F
T
F
T
F
T
T
F
F
F
CMSC 203 - Discrete Structures
15
Implication (if - then)
Binary Operator, Symbol: 
Spring 2003
P
Q
P Q
T
T
T
T
F
F
F
T
T
F
F
T
CMSC 203 - Discrete Structures
16
Biconditional (if and only if)
Binary Operator, Symbol: 
Spring 2003
P
Q
P Q
T
T
T
T
F
F
F
T
F
F
F
T
CMSC 203 - Discrete Structures
17
Statements and Operators
Statements and operators can be combined in any
way to form new statements.
P
Q
P
Q
(P)(
Q)
T
T
F
F
F
T
F
F
T
T
F
T
T
F
T
F
F
T
T
T
Spring 2003
CMSC 203 - Discrete Structures
18
Statements and Operations
Statements and operators can be combined in any
way to form new statements.
(P)(
Q)
P
Q
T
T
T
F
F
T
F
F
T
T
F
T
F
T
T
F
F
F
T
T
Spring 2003
PQ  (PQ)
CMSC 203 - Discrete Structures
19
Exercises
• To take discrete mathematics, you must have
taken calculus or a course in computer science.
• When you buy a new car from Acme Motor
Company, you get $2000 back in cash or a 2%
car loan.
• School is closed if more than 2 feet of snow
falls or if the wind chill is below -100.
Spring 2003
CMSC 203 - Discrete Structures
20
Equivalent Statements
(P)(Q (PQ) ( P)(
)
Q)
P
Q

(PQ)
T
T
F
F
T
T
F
T
T
T
F
T
T
T
T
F
F
T
T
T
The statements  (PQ) and ( P)  ( Q) are logically
equivalent, since they have the same truth table, or put
it in another way, (PQ)  ( P)  ( Q) is always
Spring 2003
CMSC 203 - Discrete Structures
21
true.
Tautologies and Contradictions
A tautology is a statement that is always true.
Examples:
– R (R)
–  (PQ)  (P)( Q)
A contradiction is a statement that is always false.
Examples:
– R(R)
–  ( (P  Q)  ( P)  ( Q))
The negation of any tautology is a contradiction, and
the negation of any contradiction is a tautology.
Spring 2003
CMSC 203 - Discrete Structures
22
Equivalence
Definition: two propositional statements
S1 and S2 are said to be (logically)
equivalent, denoted S1  S2 if
– They have the same truth table, or
– S1  S2 is a tautology
Equivalence can be established by
– Constructing truth tables
– Using equivalence laws (Table 5 in Section 1.2)
Spring 2003
CMSC 203 - Discrete Structures
23
Equivalence
Equivalence laws
–
–
–
–
–
–
–
–
–
Identity laws,
Domination laws,
Idempotent laws,
Double negation law,
Commutative laws,
Associative laws,
Distributive laws,
De Morgan’s laws,
Law with implication
Spring 2003
P  T  P,
P  F  F,
P  P  P,
 ( P)  P
P  Q  Q  P,
P  (Q  R) (P  Q)  R,
P  (Q  R) (P  Q)  (P  R),
 (PQ)  ( P)  ( Q)
P Q PQ
CMSC 203 - Discrete Structures
24
Exercises
• Show that P  Q   P  Q: by truth table
• Show that (P  Q)  (P  R)  P  (Q  R):
by equivalence laws (q20, p27):
– Law with implication on both sides
– Distribution law on LHS
Spring 2003
CMSC 203 - Discrete Structures
25
Summary, Sections 1.1, 1.2
• Proposition
• Truth value
• Truth table
• Operators and their truth tables
• Equivalence of propositional statements
– Definition
– Proving equivalence (by truth table or equivalence
laws)
Spring 2003
CMSC 203 - Discrete Structures
26
Propositional Functions &
Predicates
Propositional function (open sentence):
statement involving one or more variables,
e.g.: x-3 > 5.
Let us call this propositional function P(x),
where P is the predicate and x is the variable.
What is the truth value of P(2) ?
false
What is the truth value of P(8) ?
false
What is the truth value of P(9) ?
true
Spring 2003
CMSC 203 - Discrete Structures
27
Propositional Functions
Let us consider the propositional function
Q(x, y, z) defined as:
x + y = z.
Here, Q is the predicate and x, y, and z are the
variables.
true
What is the truth value of Q(2, 3, 5) ?
What is the truth value of Q(0, 1, 2) ?
What is the truth value of Q(9, -9, 0) ?
false
true
A propositional function (predicate) becomes a
proposition when all its variables are instantiated.
Spring 2003
CMSC 203 - Discrete Structures
28
Universal Quantification
Let P(x) be a predicate (propositional function).
Universally quantified sentence:
For all x in the universe of discourse P(x) is true.
Using the universal quantifier :
x P(x) “for all x P(x)” or “for every x P(x)”
(Note: x P(x) is either true or false, so it is a
proposition, not a propositional function.)
Spring 2003
CMSC 203 - Discrete Structures
29
Universal Quantification
Example: Let the universe of discourse be all
people
S(x): x is a UMBC student.
G(x): x is a genius.
What does x (S(x)  G(x)) mean ?
“If x is a UMBC student, then x is a genius.” or
“All UMBC students are geniuses.”
If the universe of discourse is all UMBC students,
then the same statement can be written as
x G(x)
Spring 2003
CMSC 203 - Discrete Structures
30
Existential Quantification
Existentially quantified sentence:
There exists an x in the universe of discourse
for which P(x) is true.
Using the existential quantifier :
x P(x) “There is an x such that P(x).”
“There is at least one x such that P(x).”
(Note: x P(x) is either true or false, so it is a
proposition, but no propositional function.)
Spring 2003
CMSC 203 - Discrete Structures
31
Existential Quantification
Example:
P(x): x is a UMBC professor.
G(x): x is a genius.
What does x (P(x)  G(x)) mean ?
“There is an x such that x is a UMBC professor
and x is a genius.”
or
“At least one UMBC professor is a genius.”
Spring 2003
CMSC 203 - Discrete Structures
32
Quantification
Another example:
Let the universe of discourse be the real numbers.
What does xy (x + y = 320) mean ?
“For every x there exists a y so that x + y = 320.”
Is it true?
yes
Is it true for the natural numbers?
no
Spring 2003
CMSC 203 - Discrete Structures
33
Disproof by Counterexample
A counterexample to x P(x) is an object c so
that P(c) is false.
Statements such as x (P(x)  Q(x)) can be
disproved by simply providing a counterexample.
Statement: “All birds can fly.”
Disproved by counterexample: Penguin.
Spring 2003
CMSC 203 - Discrete Structures
34
Negation
 (x P(x)) is logically equivalent to x ( P(x)).
 (x P(x)) is logically equivalent to x ( P(x)).
See Table 2 in Section 1.3.
This is de Morgan’s law for quantifiers
Spring 2003
CMSC 203 - Discrete Structures
35
Nested Quantifier
A predicate can have more than one variables.
– S(x, y, z): z is the sum of x and y
– F(x, y): x and y are friends
We can quantify individual variables in different
ways
– x, y, z (S(x, y, z)  (x <= z  y <= z))
– x y z (F(x, y)  F(x, z)  (y != z)   F(y, z)
Exercise: translate the following English
sentence into logical expression
“There is a rational number in between every pair of
distinct rational numbers”
Spring 2003
CMSC 203 - Discrete Structures
36
Summary, Sections 1.3, 1.4
• Propositional functions (predicates)
• Universal and existential quantifiers,
and the duality of the two
• When predicates become propositions
• Nested quantifiers
• Logical expressions formed by
predicates, operators, and quantifiers
Spring 2003
CMSC 203 - Discrete Structures
37
Let’s proceed to…
Mathematical
Reasoning
Spring 2003
CMSC 203 - Discrete Structures
38
Mathematical Reasoning
We need mathematical reasoning to
• determine whether a mathematical argument is
correct or incorrect and
• construct mathematical arguments.
Mathematical reasoning is not only important for
conducting proofs and program verification, but
also for artificial intelligence systems (drawing
logical inferences from knowledge and facts).
Spring 2003
CMSC 203 - Discrete Structures
39
Terminology
An axiom is a basic assumption about
mathematical structured that needs no proof.
We can use a proof to demonstrate that a
particular statement is true. A proof consists of a
sequence of statements that form an argument.
The steps that connect the statements in such a
sequence are the rules of inference.
Cases of incorrect reasoning are called fallacies.
Spring 2003
CMSC 203 - Discrete Structures
40
Terminology
A theorem is a statement that can be shown to be
true.
A lemma is a simple theorem used as an
intermediate result in the proof of another
theorem.
A corollary is a proposition that follows directly
from a theorem that has been proved.
A conjecture is a statement whose truth value is
unknown. Once it is proven, it becomes a theorem.
Spring 2003
CMSC 203 - Discrete Structures
41
Rules of Inference
Rules of inference provide the justification of
the steps used in a proof.
One important rule is called modus ponens or the
law of detachment. It is based on the tautology
(p  (p  q))  q. We write it in the following
way:
The two hypotheses p and p  q are
p
written in a column, and the conclusion
p  q below a bar, where  means “therefore”.
____
q
Spring 2003
CMSC 203 - Discrete Structures
42
Rules of Inference
The general form of a rule of inference is:
p1
p2
.
.
.
pn
____
q
Spring 2003
The rule states that if p1 and p2 and …
and pn are all true, then q is true as well.
These rules of inference can be used in
any mathematical argument and do not
require any proof.
CMSC 203 - Discrete Structures
43
Rules of Inference
p
_____
Addition
 pq
q
p  q Modus
_____ tollens
p
pq
_____
Simplification
p
p q
q r
_____
 p
r
pq
p
_____
q
p
q
_____ Conjunction
 pq
Spring 2003
CMSC 203 - Discrete Structures
Hypothetical
syllogism
Disjunctive
syllogism
44
Arguments
Just like a rule of inference, an argument consists
of one or more hypotheses (or premises) and a
conclusion.
We say that an argument is valid, if whenever all
its hypotheses are true, its conclusion is also true.
However, if any hypothesis is false, even a valid
argument can lead to an incorrect conclusion.
Proof: show that hypotheses  conclusion is true
using rules of inference
Spring 2003
CMSC 203 - Discrete Structures
45
Arguments
Example:
“If 101 is divisible by 3, then 1012 is divisible by 9.
101 is divisible by 3. Consequently, 1012 is divisible
by 9.”
Although the argument is valid, its conclusion is
incorrect, because one of the hypotheses is false
(“101 is divisible by 3.”).
If in the above argument we replace 101 with 102,
we could correctly conclude that 1022 is divisible
by 9.
Spring 2003
CMSC 203 - Discrete Structures
46
Arguments
Which rule of inference was used in the last
argument?
p: “101 is divisible by 3.”
q: “1012 is divisible by 9.”
p
p  q Modus
_____ ponens
q
Unfortunately, one of the hypotheses (p) is false.
Therefore, the conclusion q is incorrect.
Spring 2003
CMSC 203 - Discrete Structures
47
Arguments
Another example:
“If it rains today, then we will not have a
barbeque today. If we do not have a barbeque
today, then we will have a barbeque tomorrow.
Therefore, if it rains today, then we will have a
barbeque tomorrow.”
This is a valid argument: If its hypotheses are
true, then its conclusion is also true.
Spring 2003
CMSC 203 - Discrete Structures
48
Arguments
Let us formalize the previous argument:
p: “It is raining today.”
q: “We will not have a barbecue today.”
r: “We will have a barbecue tomorrow.”
So the argument is of the following form:
p q
q  r Hypothetical
______ syllogism
P
r
Spring 2003
CMSC 203 - Discrete Structures
49
Arguments
Another example:
Gary is either intelligent or a good actor.
If Gary is intelligent, then he can count
from 1 to 10.
Gary can only count from 1 to 3.
Therefore, Gary is a good actor.
i: “Gary is intelligent.”
a: “Gary is a good actor.”
c: “Gary can count from 1 to 10.”
Spring 2003
CMSC 203 - Discrete Structures
50
Arguments
i: “Gary is intelligent.”
a: “Gary is a good actor.”
c: “Gary can count from 1 to 10.”
Step
Step
Step
Step
Step
1:
2:
3:
4:
5:
c
i c
i
ai
a
Hypothesis
Hypothesis
Modus tollens Steps 1 & 2
Hypothesis
Disjunctive Syllogism
Steps 3 & 4
Conclusion: a (“Gary is a good actor.”)
Spring 2003
CMSC 203 - Discrete Structures
51
Arguments
Yet another example:
If you listen to me, you will pass CS 320.
You passed CS 320.
Therefore, you have listened to me.
Is this argument valid?
No, it assumes ((p  q) q)  p.
This statement is not a tautology. It is false if p
is false and q is true.
Spring 2003
CMSC 203 - Discrete Structures
52
Rules of Inference for Quantified Statements
x P(x)
__________
 P(c) if cU
Universal
instantiation
P(c) for an arbitrary cU
___________________
 x P(x)
Universal
generalization
x P(x)
______________________
 P(c) for some element cU
Existential
instantiation
P(c) for some element cU
____________________
 x P(x)
Existential
generalization
Spring 2003
CMSC 203 - Discrete Structures
53
Rules of Inference for Quantified Statements
Example:
Every UMB student is a genius.
George is a UMB student.
Therefore, George is a genius.
U(x): “x is a UMB student.”
G(x): “x is a genius.”
Spring 2003
CMSC 203 - Discrete Structures
54
Rules of Inference for Quantified Statements
The following steps are used in the argument:
Step 1: x (U(x)  G(x))
Hypothesis
Step 2: U(George)  G(George) Univ. instantiation
using Step 1
Step 3: U(George)
Hypothesis
Step 4: G(George)
Modus ponens
using Steps 2 & 3
x P(x)
__________
 P(c) if cU
Spring 2003
Universal
instantiation
CMSC 203 - Discrete Structures
55
Proving Theorems
Direct proof:
An implication p  q can be proved by showing
that if p is true, then q is also true.
Example: Give a direct proof of the theorem
“If n is odd, then n2 is odd.”
Idea: Assume that the hypothesis of this
implication is true (n is odd). Then use rules of
inference and known theorems of math to show
that q must also be true (n2 is odd).
Spring 2003
CMSC 203 - Discrete Structures
56
Proving Theorems
n is odd.
Then n = 2k + 1, where k is an integer.
Consequently, n2 = (2k + 1)2.
= 4k2 + 4k + 1
= 2(2k2 + 2k) + 1
Since n2 can be written in this form, it is odd.
Spring 2003
CMSC 203 - Discrete Structures
57
Proving Theorems
Indirect proof:
An implication p  q is equivalent to its contrapositive  q   p. Therefore, we can prove p 
q by showing that whenever q is false, then p is
also false.
Example: Give an indirect proof of the theorem
“If 3n + 2 is odd, then n is odd.”
Idea: Assume that the conclusion of this
implication is false (n is even). Then use rules of
inference and known theorems to show that p
must also be false (3n + 2 is even).
Spring 2003
CMSC 203 - Discrete Structures
58
Proving Theorems
n is even.
Then n = 2k, where k is an integer.
It follows that 3n + 2 = 3(2k) + 2
= 6k + 2
= 2(3k + 1)
Therefore, 3n + 2 is even.
We have shown that the contrapositive of the
implication is true, so the implication itself is also
true (If 2n + 3 is odd, then n is odd).
Spring 2003
CMSC 203 - Discrete Structures
59
Summary, Section 1.5
• Terminology (axiom, theorem, conjecture,
etc.)
• Rules of inference (Tables 1 and 2)
• Valid argument (hypotheses and conclusion)
• Construction of valid argument using rules of
inference
• Direct and indirect proofs
• Other proof methods (e.g., induction, pigeon
hole) will be introduced in later chapters
Spring 2003
CMSC 203 - Discrete Structures
60
…
and now for something
completely different…
Set Theory
Actually, you will see that logic and
set theory are very closely related.
Spring 2003
CMSC 203 - Discrete Structures
61
Set Theory
• Set: Collection of objects (“elements”)
• aA
“a is an element of A”
“a is a member of A”
• aA
“a is not an element of A”
• A = {a1, a2, …, an} “A contains a1, …, an”
• Order of elements is insignificant
• It does not matter how often the same
element is listed.
Spring 2003
CMSC 203 - Discrete Structures
62
Set Equality
Sets A and B are equal if and only if they
contain exactly the same elements.
Examples:
• A = {9, 2, 7, -3}, B = {7, 9, -3, 2} :
A=B
• A = {dog, cat, horse},
B = {cat, horse, squirrel, dog} :
AB
• A = {dog, cat, horse},
B = {cat, horse, dog, dog} :
A=B
Spring 2003
CMSC 203 - Discrete Structures
63
Examples for Sets
“Standard” Sets:
• Natural numbers N = {0, 1, 2, 3, …}
• Integers Z = {…, -2, -1, 0, 1, 2, …}
• Positive Integers Z+ = {1, 2, 3, 4, …}
• Real Numbers R = {47.3, -12, , …}
• Rational Numbers Q = {1.5, 2.6, -3.8, 15, …}
(correct definitions will follow)
Spring 2003
CMSC 203 - Discrete Structures
64
Examples for Sets
• A=
“empty set/null set”
• A = {z}
Note: zA, but z  {z}
• A = {{b, c}, {c, x, d}}
• A = {{x, y}}
Note: {x, y} A, but {x, y}  {{x, y}}
• A = {x | P(x)}
“set of all x such that P(x)”
• A = {x | x N  x > 7} = {8, 9, 10, …}
“set builder notation”
Spring 2003
CMSC 203 - Discrete Structures
65
Examples for Sets
We are now able to define the set of rational
numbers Q:
Q = {a/b | aZ  bZ+}, or
Q = {a/b | aZ  bZ  b0}
And how about the set of real numbers R?
R = {r | r is a real number}
That is the best we can do. It can neither be
defined by enumeration or builder function.
Spring 2003
CMSC 203 - Discrete Structures
66
Subsets
AB
“A is a subset of B”
A  B if and only if every element of A is also
an element of B.
We can completely formalize this:
A  B  x (xA  xB)
Examples:
AB?
true
A = {3, 3, 3, 9}, B = {5, 9, 1, 3}, A  B ?
true
A = {1, 2, 3}, B = {2, 3, 4},
false
A = {3, 9}, B = {5, 9, 1, 3},
Spring 2003
CMSC 203 - Discrete Structures
AB?
67
Subsets
Useful rules:
• A = B  (A  B)  (B  A)
• (A  B)  (B  C)  A  C (see Venn
Diagram)
U
B
Spring 2003
A
C
CMSC 203 - Discrete Structures
68
Subsets
Useful rules:
•   A for any set A
• A  A for any set A
Proper subsets:
A  B “A is a proper subset of B”
A  B  x (xA  xB)  x (xB  xA)
or
A  B  x (xA  xB)  x (xB 
xA)
Spring 2003
CMSC 203 - Discrete Structures
69
Cardinality of Sets
If a set S contains n distinct elements, nN,
we call S a finite set with cardinality n.
Examples:
A = {Mercedes, BMW, Porsche}, |A| = 3
B = {1, {2, 3}, {4, 5}, 6}
|B| = 4
C=
|C| = 0
D = { xN | x  7000 }
|D| = 7001
E = { xN | x  7000 }
E is infinite!
Spring 2003
CMSC 203 - Discrete Structures
70
The Power Set
P(A)
“power set of A” (also written as 2A)
P(A) = {B | B  A}
(contains all subsets of A)
Examples:
A = {x, y, z}
P(A) = {, {x}, {y}, {z}, {x, y}, {x, z}, {y, z}, {x, y, z}}
A=
P(A) = {}
Note: |A| = 0, |P(A)| = 1
Spring 2003
CMSC 203 - Discrete Structures
71
The Power Set
Cardinality of power sets: | P(A) | = 2|A|
• Imagine each element in A has an “on/off” switch
• Each possible switch configuration in A
corresponds to one subset of A, thus one element
in P(A)
A
x
y
z
1
x
y
z
2
x
y
z
3
x
y
z
4
x
y
z
5
x
y
z
6
x
y
z
7
x
y
z
8
x
y
z
• For 3 elements in A, there are
222 = 8 elements in P(A)
Spring 2003
CMSC 203 - Discrete Structures
72
Cartesian Product
The ordered n-tuple (a1, a2, a3, …, an) is an
ordered collection of n objects.
Two ordered n-tuples (a1, a2, a3, …, an) and
(b1, b2, b3, …, bn) are equal if and only if they
contain exactly the same elements in the same
order, i.e. ai = bi for 1  i  n.
The Cartesian product of two sets is defined as:
AB = {(a, b) | aA  bB}
Spring 2003
CMSC 203 - Discrete Structures
73
Cartesian Product
Example:
A = {good, bad}, B = {student, prof}
AB = {
(good, student), (good, prof), (bad, student), (bad, prof)}
BA = { (student, good),
}
(prof, good), (student, bad), (prof, bad)
Example: A = {x, y}, B = {a, b, c}
AB = {(x, a), (x, b), (x, c), (y, a), (y, b), (y, c)}
Spring 2003
CMSC 203 - Discrete Structures
74
Cartesian Product
Note that:
• A = 
• A = 
• For non-empty sets A and B: AB  AB  BA
• |AB| = |A||B|
The Cartesian product of two or more sets is
defined as:
A1A2…An = {(a1, a2, …, an) | aiA for 1  i  n}
Spring 2003
CMSC 203 - Discrete Structures
75
Set Operations
Union: AB = {x | xA  xB}
Example: A = {a, b}, B = {b, c, d}
AB = {a, b, c, d}
Intersection: AB = {x | xA  xB}
Example: A = {a, b}, B = {b, c, d}
AB = {b}
Spring 2003
CMSC 203 - Discrete Structures
76
Set Operations
Two sets are called disjoint if their intersection
is empty, that is, they share no elements:
AB = 
The difference between two sets A and B
contains exactly those elements of A that are
not in B:
A-B = {x | xA  xB}
Example: A = {a, b}, B = {b, c, d}, A-B = {a}
Spring 2003
CMSC 203 - Discrete Structures
77
Set Operations
The complement of a set A contains exactly
those elements under consideration that are not
in A:
Ac = U-A
Example: U = N, B = {250, 251, 252, …}
Bc = {0, 1, 2, …, 248, 249}
Spring 2003
CMSC 203 - Discrete Structures
78
Set Identity
Table 1 in Section 1.7 shows many useful equations
How can we prove A(BC) = (AB)(AC)?
Method I: logical equivalent
xA(BC)
 xA  x(BC)
 xA  (xB  xC)
 (xA  xB)  (xA  xC) (distributive law)
 x(AB)  x(AC)
 x(AB)(AC)
Every logical expression can be transformed into an
equivalent expression in set theory and vice versa.
Spring 2003
CMSC 203 - Discrete Structures
79
Set Operations
Method II: Membership table
1 means “x is an element of this set”
0 means “x is not an element of this set”
A B C BC
A(BC)
AB
AC
(AB) (AC)
0 0 0
0
0
0
0
0
0 0 1
0
0
0
1
0
0 1 0
0
0
1
0
0
0 1 1
1
1
1
1
1
1 0 0
0
1
1
1
1
1 0 1
0
1
1
1
1
1 1 0
0
1
1
1
1
1 1 1
1
1
1
1
1
Spring 2003
CMSC 203 - Discrete Structures
80
… and the following mathematical
appetizer is about…
Functions
Spring 2003
CMSC 203 - Discrete Structures
81
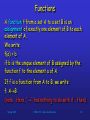
Functions
A function f from a set A to a set B is an
assignment of exactly one element of B to each
element of A.
We write
f(a) = b
if b is the unique element of B assigned by the
function f to the element a of A.
If f is a function from A to B, we write
f: AB
(note: Here, ““ has nothing to do with if… then)
Spring 2003
CMSC 203 - Discrete Structures
82
Functions
If f:AB, we say that A is the domain of f and B
is the codomain of f.
If f(a) = b, we say that b is the image of a and a is
the pre-image of b.
The range of f:AB is the set of all images of
elements of A.
We say that f:AB maps A to B.
Spring 2003
CMSC 203 - Discrete Structures
83
Functions
Let us take a look at the function f:PC with
P = {Linda, Max, Kathy, Peter}
C = {Boston, New York, Hong Kong, Moscow}
f(Linda) = Moscow
f(Max) = Boston
f(Kathy) = Hong Kong
f(Peter) = New York
Here, the range of f is C.
Spring 2003
CMSC 203 - Discrete Structures
84
Functions
Let us re-specify f as follows:
f(Linda) = Moscow
f(Max) = Boston
f(Kathy) = Hong Kong
f(Peter) = Boston
Is f still a function? yes
What is its range?
Spring 2003
{Moscow, Boston, Hong Kong}
CMSC 203 - Discrete Structures
85
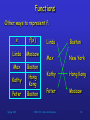
Functions
Other ways to represent f:
x
f(x)
Linda
Moscow
Max
Boston
Kathy
Hong
Kong
Peter
Boston
Spring 2003
Linda
Boston
Max
New York
Kathy
Hong Kong
Peter
Moscow
CMSC 203 - Discrete Structures
86
Functions
If the domain of our function f is large, it is
convenient to specify f with a formula, e.g.:
f:RR
f(x) = 2x
This leads to:
f(1) = 2
f(3) = 6
f(-3) = -6
…
Spring 2003
CMSC 203 - Discrete Structures
87
Functions
Let f1 and f2 be functions from A to R.
Then the sum and the product of f1 and f2 are
also functions from A to R defined by:
(f1 + f2)(x) = f1(x) + f2(x)
(f1f2)(x) = f1(x) f2(x)
Example:
f1(x) = 3x, f2(x) = x + 5
(f1 + f2)(x) = f1(x) + f2(x) = 3x + x + 5 = 4x + 5
(f1f2)(x) = f1(x) f2(x) = 3x (x + 5) = 3x2 + 15x
Spring 2003
CMSC 203 - Discrete Structures
88
Functions
We already know that the range of a function
f:AB is the set of all images of elements aA.
If we only regard a subset SA, the set of all
images of elements sS is called the image of S.
We denote the image of S by f(S):
f(S) = {f(s) | sS}
Spring 2003
CMSC 203 - Discrete Structures
89
Functions
Let us look at the following well-known function:
f(Linda) = Moscow
f(Max) = Boston
f(Kathy) = Hong Kong
f(Peter) = Boston
What is the image of S = {Linda, Max} ?
f(S) = {Moscow, Boston}
What is the image of S = {Max, Peter} ?
f(S) = {Boston}
Spring 2003
CMSC 203 - Discrete Structures
90
Properties of Functions
A function f:AB is said to be one-to-one (or
injective), if and only if
x, yA (f(x) = f(y)  x = y)
In other words: f is one-to-one if and only if it
does not map two distinct elements of A onto the
same element of B.
Spring 2003
CMSC 203 - Discrete Structures
91
Properties of Functions
And again…
f(Linda) = Moscow
f(Max) = Boston
f(Kathy) = Hong Kong
f(Peter) = Boston
g(Linda) = Moscow
g(Max) = Boston
g(Kathy) = Hong Kong
g(Peter) = New York
Is f one-to-one?
Is g one-to-one?
No, Max and Peter are
mapped onto the same
element of the image.
Yes, each element is
assigned a unique
element of the image.
Spring 2003
CMSC 203 - Discrete Structures
92
Properties of Functions
How can we prove that a function f is one-to-one?
Whenever you want to prove something, first
take a look at the relevant definition(s):
x, yA (f(x) = f(y)  x = y)
Example:
f:RR
f(x) = x2
Disproof by counterexample:
f(3) = f(-3), but 3  -3, so f is not one-to-one.
Spring 2003
CMSC 203 - Discrete Structures
93
Properties of Functions
… and yet another example:
f:RR
f(x) = 3x
One-to-one: x, yA (f(x) = f(y)  x = y)
To show: f(x)  f(y) whenever x  y
xy
 3x  3y
 f(x)  f(y),
so if x  y, then f(x)  f(y), that is, f is one-to-one.
Spring 2003
CMSC 203 - Discrete Structures
94
Properties of Functions
A function f:AB with A,B  R is called strictly
increasing, if
x,yA (x < y  f(x) < f(y)),
and strictly decreasing, if
x,yA (x < y  f(x) > f(y)).
Obviously, a function that is either strictly
increasing or strictly decreasing is one-to-one.
Spring 2003
CMSC 203 - Discrete Structures
95
Properties of Functions
A function f:AB is called onto, or surjective, if
and only if for every element bB there is an
element aA with f(a) = b.
In other words, f is onto if and only if its range is
its entire codomain.
A function f: AB is a one-to-one correspondence,
or a bijection, if and only if it is both one-to-one
and onto.
Obviously, if f is a bijection and A and B are finite
sets, then |A| = |B|.
Spring 2003
CMSC 203 - Discrete Structures
96
Properties of Functions
Examples:
In the following examples, we use the arrow
representation to illustrate functions f:AB.
In each example, the complete sets A and B are
shown.
Spring 2003
CMSC 203 - Discrete Structures
97
Properties of Functions
Linda
Boston
Max
New York
Kathy
Hong Kong
Peter
Moscow
Spring 2003
Is f injective?
No.
Is f surjective?
No.
Is f bijective?
No.
CMSC 203 - Discrete Structures
98
Properties of Functions
Linda
Boston
Max
New York
Kathy
Hong Kong
Peter
Moscow
Is f injective?
No.
Is f surjective?
Yes.
Is f bijective?
No.
Paul
Spring 2003
CMSC 203 - Discrete Structures
99
Properties of Functions
Linda
Boston
Max
New York
Kathy
Hong Kong
Peter
Moscow
Is f injective?
Yes.
Is f surjective?
No.
Is f bijective?
No.
Lübeck
Spring 2003
CMSC 203 - Discrete Structures
100
Properties of Functions
Linda
Boston
Max
New York
Kathy
Hong Kong
Peter
Moscow
Is f injective?
No! f is not even
a function!
Lübeck
Spring 2003
CMSC 203 - Discrete Structures
101
Properties of Functions
Linda
Boston
Max
New York
Kathy
Hong Kong
Peter
Moscow
Helena
Lübeck
Spring 2003
Is f injective?
Yes.
Is f surjective?
Yes.
Is f bijective?
Yes.
CMSC 203 - Discrete Structures
102
Inversion
An interesting property of bijections is that
they have an inverse function.
The inverse function of the bijection f:AB
is the function f-1:BA with
f-1(b) = a whenever f(a) = b.
Spring 2003
CMSC 203 - Discrete Structures
103
Inversion
Example:
The inverse function
f-1 is given by:
f(Linda) = Moscow
f(Max) = Boston
f(Kathy) = Hong Kong
f(Peter) = Lübeck
f(Helena) = New York
f-1(Moscow) = Linda
f-1(Boston) = Max
f-1(Hong Kong) = Kathy
f-1(Lübeck) = Peter
f-1(New York) = Helena
Clearly, f is bijective.
Inversion is only
possible for bijections
(= invertible functions)
Spring 2003
CMSC 203 - Discrete Structures
104
Inversion
Linda
Boston
f
Max
New York
f-1
Kathy
Hong Kong
Peter
Moscow
Helena
Lübeck
Spring 2003
f-1:CP is no
function, because
it is not defined
for all elements of
C and assigns two
images to the preimage New York.
CMSC 203 - Discrete Structures
105
Composition
The composition of two functions g:AB and
f:BC, denoted by fg, is defined by
(fg)(a) = f(g(a))
This means that
• first, function g is applied to element aA,
mapping it onto an element of B,
• then, function f is applied to this element of
B, mapping it onto an element of C.
• Therefore, the composite function maps
from A to C.
Spring 2003
CMSC 203 - Discrete Structures
106
Composition
Example:
f(x) = 7x – 4, g(x) = 3x,
f:RR, g:RR
(fg)(5) = f(g(5)) = f(15) = 105 – 4 = 101
(fg)(x) = f(g(x)) = f(3x) = 21x - 4
Spring 2003
CMSC 203 - Discrete Structures
107
Composition
Composition of a function and its inverse:
(f-1f)(x) = f-1(f(x)) = x
The composition of a function and its inverse
is the identity function i(x) = x.
Spring 2003
CMSC 203 - Discrete Structures
108
Graphs
The graph of a function f:AB is the set of
ordered pairs {(a, b) | aA and f(a) = b}.
The graph is a subset of AB that can be used
to visualize f in a two-dimensional coordinate
system.
Spring 2003
CMSC 203 - Discrete Structures
109
Floor and Ceiling Functions
The floor and ceiling functions map the real
numbers onto the integers (RZ).
The floor function assigns to rR the largest
zZ with z  r, denoted by r.
Examples: 2.3 = 2, 2 = 2, 0.5 = 0, -3.5 = -4
The ceiling function assigns to rR the smallest
zZ with z  r, denoted by r.
Examples: 2.3 = 3, 2 = 2, 0.5 = 1, -3.5 = -3
Spring 2003
CMSC 203 - Discrete Structures
110
Exercises
I recommend Exercises 1 and 15 in Section 1.6.
It may also be useful to study the graph displays
in that section.
Another question: What do all graph displays for
any function f:RR have in common?
Spring 2003
CMSC 203 - Discrete Structures
111