* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 1 PHYSICS 231 Lecture 21: Some material science
Diamond anvil cell wikipedia , lookup
Spinodal decomposition wikipedia , lookup
Creep (deformation) wikipedia , lookup
Colloidal crystal wikipedia , lookup
Dislocation wikipedia , lookup
State of matter wikipedia , lookup
Fluid dynamics wikipedia , lookup
Acoustic metamaterial wikipedia , lookup
Fracture mechanics wikipedia , lookup
Sol–gel process wikipedia , lookup
Cauchy stress tensor wikipedia , lookup
Stress (mechanics) wikipedia , lookup
Strengthening mechanisms of materials wikipedia , lookup
Viscoplasticity wikipedia , lookup
Hooke's law wikipedia , lookup
Fatigue (material) wikipedia , lookup
Deformation (mechanics) wikipedia , lookup
Paleostress inversion wikipedia , lookup
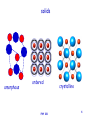
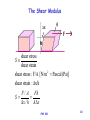
PHYSICS 231 Lecture 21: Some material science gas liquid solid Remco Zegers Walk-in hour: Thursday 11:30-13:30 am Helproom PHY 231 1 Solid States of matter Liquid Gas Plasma difficult to deform difficult to compress difficult to flow easy to deform easy to deform easy to deform difficult to compress easy to flow easy to easy to compress compress easy to flow easy to flow not charged not charged not charged charged PHY 231 2 Phase transformations PHY 231 3 solids amorphous ordered PHY 231 crystalline 4 The deformation of solids Stress: Tells something about the force causing the deformation Strain: Measure of the degree of deformation For small stress, strain and stress are linearly correlated. Strain = Constant*Stress Constant: elastic modulus The elastic modulus depends on: • Material that is deformed • Type of deformation (a different modulus is defined for different types of deformations) PHY 231 5 The Young’s modulus tensile stress Y tensile strain 2 tensile stress : F/A [N/m Pascal (Pa)] tensile strain : L/L 0 FL0 F/A Y L / L0 AL Beyond the elastic limit an object is permanently deformed (it does not return to its original shape if the stress is removed). PHY 231 6 example An architect wants to design a 5m high circular pillar with a radius of 0.5 m that holds a bronze statue that weighs 1.0E+04 kg. He chooses concrete for the material of the pillar (Y=1.0E+10 Pa). How much does the pillar compress? 5m PHY 231 7 Ultimate strength Ultimate strength: maximum force per unit area a material can withstand before it breaks or fractures. Different for compression and tension. PHY 231 8 example A builder is stacking 1 m3 cubic concrete blocks. Each blocks weighs 5E+03 kg. The ultimate strength of concrete for compression is 2E+07 Pa. How many blocks can he stack before the lowest block is crushed? PHY 231 9 The Shear Modulus x shear stress S shear strain 2 shear stress : F/A [N/m Pascal (Pa)] shear strain : x/h F/A Fh S x / h Ax PHY 231 10 Moving earth crust 100 m 30 m A tectonic plate in the lower crust (100 m deep) of the earth is shifted during an earthquake by 30m. What is the shear stress involved, if the upper layer of the earth does not move? (S=1.5E+10 Pa) PHY 231 11 Bulk Modulus volume stress B volume strain volume stress : F/A [N/m 2 Pascal (Pa)] volume strain : V/V0 F / A P B V / V0 V / V0 P pressure Compressibility: 1/(Bulk modulus) PHY 231 12 example What force per unit area needs to be applied to compress 1 m3 water by 1%? (B=0.21E+10 Pa) PHY 231 13 Some typical elastic moduli PHY 231 14 Density M V 3 (kg / m ) specific material / water ( 4 PHY 231 o C) 15 Pressure Pressure=F/A (N/m2=Pa) Same Force, different pressure PHY 231 16 example A nail is driven into a piece of wood with a force of 700N. What is the pressure on the wood if Anail=1 mm2? A person (weighing 700 N) is lying on a bed of such nails (his body covers 1000 nails). What is the pressure exerted by each of the nails? PHY 231 17